NLP系列_朴素贝叶斯实战与进阶

Posted 2020-06-13 龙心尘

作者： 寒小阳 && 龙心尘
时间：2016年2月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/50629608
http://blog.csdn.net/longxinchen_ml/article/details/50629613
声明：版权所有，转载请联系作者并注明出处

1.引言

前两篇博文介绍了朴素贝叶斯这个名字读着"萌蠢"但实际上简单直接高效的方法，我们也介绍了一下贝叶斯方法的一些细节。按照老规矩，『锄头』给你了，得负责教教怎么用和注意事项，也顺便带大家去除除草对吧。恩，此节作为更贴近实际应用的部分，将介绍贝叶斯方法的优缺点、常见适用场景和可优化点，然后找点实际场景撸点例子练练手，看看工具怎么用。

PS：本文所有的python代码和ipython notebook已整理至github相应页面，欢迎下载和尝试。

2.贝叶斯方法优缺点

既然讲的是朴素贝叶斯，那博主保持和它一致的风格，简单直接高效地丢干货了：

• 优点

1. 对待预测样本进行预测，过程简单速度快(想想邮件分类的问题，预测就是分词后进行概率乘积，在log域直接做加法更快)。
2. 对于多分类问题也同样很有效，复杂度也不会有大程度上升。
3. 在分布独立这个假设成立的情况下，贝叶斯分类器效果奇好，会略胜于逻辑回归，同时我们需要的样本量也更少一点。
4. 对于类别类的输入特征变量，效果非常好。对于数值型变量特征，我们是默认它符合正态分布的。

• 缺点

1. 对于测试集中的一个类别变量特征，如果在训练集里没见过，直接算的话概率就是0了，预测功能就失效了。当然，我们前面的文章提过我们有一种技术叫做**『平滑』操作**，可以缓解这个问题，最常见的平滑技术是拉普拉斯估测。
2. 那个…咳咳，朴素贝叶斯算出的概率结果，比较大小还凑合，实际物理含义…恩，别太当真。
3. 朴素贝叶斯有分布独立的假设前提，而现实生活中这些predictor很难是完全独立的。

3.最常见应用场景

• 文本分类/垃圾文本过滤/情感判别：这大概会朴素贝叶斯应用做多的地方了，即使在现在这种分类器层出不穷的年代，在文本分类场景中，朴素贝叶斯依旧坚挺地占据着一席之地。原因嘛，大家知道的，因为多分类很简单，同时在文本数据中，分布独立这个假设基本是成立的。而垃圾文本过滤(比如垃圾邮件识别)和情感分析(微博上的褒贬情绪)用朴素贝叶斯也通常能取得很好的效果。
• 多分类实时预测：这个是不是不能叫做场景？对于文本相关的多分类实时预测，它因为上面提到的优点，被广泛应用，简单又高效。
• 推荐系统：是的，你没听错，是用在推荐系统里！！朴素贝叶斯和协同过滤(Collaborative Filtering)是一对好搭档，协同过滤是强相关性，但是泛化能力略弱，朴素贝叶斯和协同过滤一起，能增强推荐的覆盖度和效果。

4.朴素贝叶斯注意点

这个部分的内容，本来应该在最后说的，不过为了把干货集中放在代码示例之前，先搁这儿了，大家也可以看完朴素贝叶斯的各种例子之后，回来再看看这些tips。

• 大家也知道，很多特征是连续数值型的，但是它们不一定服从正态分布，一定要想办法把它们变换调整成满足正态分布！！
• 对测试数据中的0频次项，一定要记得平滑，简单一点可以用『拉普拉斯平滑』。
• 先处理处理特征，把相关特征去掉，因为高相关度的2个特征在模型中相当于发挥了2次作用。
• 朴素贝叶斯分类器一般可调参数比较少，比如scikit-learn中的朴素贝叶斯只有拉普拉斯平滑因子alpha，类别先验概率class_prior和预算数据类别先验fit_prior。模型端可做的事情不如其他模型多，因此我们还是集中精力进行数据的预处理，以及特征的选择吧。
• 那个，一般其他的模型(像logistic regression，SVM等)做完之后，我们都可以尝试一下bagging和boosting等融合增强方法。咳咳，很可惜，对朴素贝叶斯里这些方法都没啥用。原因？原因是这些融合方法本质上是减少过拟合，减少variance的。朴素贝叶斯是没有variance可以减小。

5. 朴素贝叶斯训练/建模

理论干货和注意点都说完了，来提提怎么快速用朴素贝叶斯训练模型吧。博主一直提倡要站在巨人的肩膀上编程(其实就是懒…同时一直很担忧写出来的代码的健壮性…)，咳咳，我们又很自然地把scikit-learn拿过来了。scikit-learn里面有3种不同类型的朴素贝叶斯：

• 高斯分布型：用于classification问题，假定属性/特征是服从正态分布的。
• 多项式型：用于离散值模型里。比如文本分类问题里面我们提到过，我们不光看词语是否在文本中出现，也得看出现的次数。如果总词数为n，出现词数为m的话，说起来有点像掷骰子n次出现m次这个词的场景。
• 伯努利型：这种情况下，就如之前博文里提到的bag of words处理方式一样，最后得到的特征只有0(没出现)和1(出现过)。

根据你的数据集，可以选择scikit-learn中以上任意一种朴素贝叶斯，我们直接举个简单的例子，用高斯分布型朴素贝叶斯建模：

# 我们直接取iris数据集，这个数据集有名到都不想介绍了...
# 其实就是根据花的各种数据特征，判定是什么花
from sklearn import datasets
iris = datasets.load_iris()
iris.data[:5]
#array([[ 5.1,  3.5,  1.4,  0.2],
#       [ 4.9,  3. ,  1.4,  0.2],
#       [ 4.7,  3.2,  1.3,  0.2],
#       [ 4.6,  3.1,  1.5,  0.2],
#       [ 5. ,  3.6,  1.4,  0.2]])

#我们假定sepal length, sepal width, petal length, petal width 4个量独立且服从高斯分布，用贝叶斯分类器建模
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
y_pred = gnb.fit(iris.data, iris.target).predict(iris.data)
right_num = (iris.target == y_pred).sum()
print("Total testing num :%d , naive bayes accuracy :%f" %(iris.data.shape[0], float(right_num)/iris.data.shape[0]))
# Total testing num :150 , naive bayes accuracy :0.960000

你看，朴素贝叶斯分类器，简单直接高效，在150个测试样本上，准确率为96%。

6.朴素贝叶斯之文本主题分类器

这是朴素贝叶斯最擅长的应用场景之一，对于不同主题的文本，我们可以用朴素贝叶斯训练一个分类器，然后将其应用在新数据上，预测主题类型。

6.1 新闻数据分类

我们使用搜狐新闻数据来实验朴素贝叶斯分类器，这部分新闻数据包括it、汽车、财经、健康等9个类别，简洁版数据解压缩后总共16289条新闻，一篇新闻一个txt，我们把数据合并到一个大文件中，一行一篇文章，同时将新闻id(指明新闻的类别)放在文章之前，然后用ICTCLAS(python的话你也可以用结巴分词)进行分词，得到以下的文本内容：

我们随机选取3/5的数据作为训练集，2/5的数据作为测试集，采用互信息对文本特征进行提取，提取出1000个左右的特征词。然后用朴素贝叶斯分类器进行训练，实际训练过程就是对于特征词，统计在训练集和各个类别出现的次数，测试阶段做预测也是扫描一遍测试集，计算相应的概率。因此整个过程非常高效，完整的运行代码如下：

# 这部分代码基本纯手撸的...没有调用开源库...大家看看就好...
#!encoding=utf-8
import sys, math, random, collections

def shuffle(inFile):
    '''
        简单的乱序操作，用于生成训练集和测试集
    '''
    textLines = [line.strip() for line in open(inFile)]
    print "正在准备训练和测试数据，请稍后..."
    random.shuffle(textLines)
    num = len(textLines)
    trainText = textLines[:3*num/5]
    testText = textLines[3*num/5:]
    print "准备训练和测试数据准备完毕，下一步..."
    return trainText, testText

#总共有9种新闻类别，我们给每个类别一个编号
lables = ['A','B','C','D','E','F','G','H','I']
def lable2id(lable):
    for i in xrange(len(lables)):
        if lable == lables[i]:
            return i
    raise Exception('Error lable %s' % (lable))

def doc_dict():
    '''
        构造和类别数等长的0向量
    '''
    return [0]*len(lables)

def mutual_info(N,Nij,Ni_,N_j):
    '''
        计算互信息，这里log的底取为2
    '''
    return Nij * 1.0 / N * math.log(N * (Nij+1)*1.0/(Ni_*N_j))/ math.log(2)
    
def count_for_cates(trainText, featureFile):
    '''
        遍历文件，统计每个词在每个类别出现的次数，和每类的文档数
        并写入结果特征文件
    '''
    docCount = [0] * len(lables)
    wordCount = collections.defaultdict(doc_dict())
    #扫描文件和计数  
    for line in trainText:
        lable,text = line.strip().split(' ',1)
        index = lable2id(lable[0])        
        words = text.split(' ')
        for word in words:
            wordCount[word][index] += 1
            docCount[index] += 1
    #计算互信息值
    print "计算互信息，提取关键/特征词中，请稍后..."
    miDict = collections.defaultdict(doc_dict())
    N = sum(docCount)
    for k,vs in wordCount.items():
        for i in xrange(len(vs)):
            N11 = vs[i]
            N10 = sum(vs) - N11
            N01 = docCount[i] - N11
            N00 = N - N11 - N10 - N01
            mi = mutual_info(N,N11,N10+N11,N01+N11) + mutual_info(N,N10,N10+N11,N00+N10)+ mutual_info(N,N01,N01+N11,N01+N00)+ mutual_info(N,N00,N00+N10,N00+N01)
            miDict[k][i] = mi
    fWords = set()
    for i in xrange(len(docCount)):
        keyf = lambda x:x[1][i]
        sortedDict = sorted(miDict.items(),key=keyf,reverse=True)
        for j in xrange(100):
            fWords.add(sortedDict[j][0])
    out = open(featureFile, 'w')
    #输出各个类的文档数目
    out.write(str(docCount)+"\\n")
    #输出互信息最高的词作为特征词
    for fword in fWords:
        out.write(fword+"\\n")
    print "特征词写入完毕..."
    out.close()
    
def load_feature_words(featureFile):
    '''
        从特征文件导入特征词
    '''
    f = open(featureFile)
    #各个类的文档数目
    docCounts = eval(f.readline())
    features = set()
    #读取特征词
    for line in f:
        features.add(line.strip())
    f.close()
    return docCounts,features
            
def train_bayes(featureFile, textFile, modelFile):
    '''
        训练贝叶斯模型，实际上计算每个类中特征词的出现次数
    '''
    print "使用朴素贝叶斯训练中..."
    docCounts,features = load_feature_words(featureFile)
    wordCount = collections.defaultdict(doc_dict())
    #每类文档特征词出现的次数
    tCount = [0]*len(docCounts)
    for line in open(textFile):
        lable,text = line.strip().split(' ',1)
        index = lable2id(lable[0])        
        words = text.split(' ')
        for word in words:
            if word in features:
                tCount[index] += 1
                wordCount[word][index] += 1
    outModel = open(modelFile, 'w')
    #拉普拉斯平滑
    print "训练完毕，写入模型..."
    for k,v in wordCount.items():
        scores = [(v[i]+1) * 1.0 / (tCount[i]+len(wordCount)) for i in xrange(len(v))]
        outModel.write(k+"\\t"+scores+"\\n")
    outModel.close()
        
def load_model(modelFile):
    '''
        从模型文件中导入计算好的贝叶斯模型
    '''
    print "加载模型中..."
    f = open(modelFile)
    scores = {}
    for line in f:
        word,counts = line.strip().rsplit('\\t',1)    
        scores[word] = eval(counts)
    f.close()
    return scores
    
def predict(featureFile, modelFile, testText):
    '''
        预测文档的类标，标准输入每一行为一个文档
    '''
    docCounts,features = load_feature_words()    
    docScores = [math.log(count * 1.0 /sum(docCounts)) for count in docCounts]
    scores = load_model(modelFile)
    rCount = 0
    docCount = 0
    print "正在使用测试数据验证模型效果..."
    for line in testText:
        lable,text = line.strip().split(' ',1)
        index = lable2id(lable[0])        
        words = text.split(' ')
        preValues = list(docScores)
        for word in words:
            if word in features:                
                for i in xrange(len(preValues)):
                    preValues[i]+=math.log(scores[word][i])
        m = max(preValues)
        pIndex = preValues.index(m)
        if pIndex == index:
            rCount += 1
        #print lable,lables[pIndex],text
        docCount += 1
    print("总共测试文本量: %d , 预测正确的类别量: %d, 朴素贝叶斯分类器准确度:%f" %(rCount,docCount,rCount * 1.0 / docCount))       
        
        
if __name__=="__main__":
    if len(sys.argv) != 4:
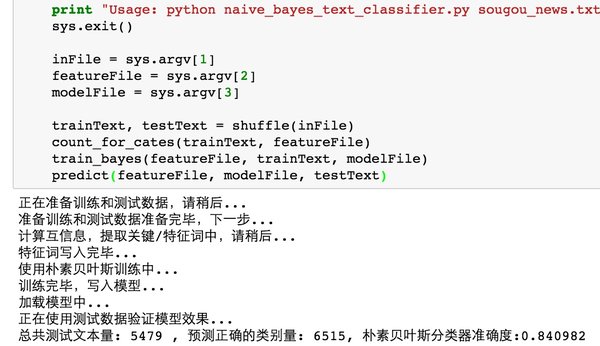
    print "Usage: python naive_bayes_text_classifier.py sougou_news.txt feature_file.out model_file.out"
    sys.exit()

    inFile = sys.argv[1]
    featureFile = sys.argv[2]
    modelFile = sys.argv[3]

    trainText, testText = shuffle(inFile)
    count_for_cates(trainText, featureFile)
    train_bayes(featureFile, trainText, modelFile)
    predict(featureFile, modelFile, testText)

6.2 分类结果

运行结果如下，在6515条数据上，9个类别的新闻上，有84.1%的准确度：

7. Kaggle比赛之『旧金山犯罪分类预测』

7.1 旧金山犯罪分类预测问题

没过瘾对吧，确实每次学完一个机器学习算法，不在实际数据上倒腾倒腾，总感觉不那么踏实(想起来高中各种理科科目都要找点题来做的感觉)。好，我们继续去Kaggle扒点场景和数据来练练手。正巧之前Kaggle上有一个分类问题，场景和数据也都比较简单，我们拿来用朴素贝叶斯试试水。问题请戳这里。

7.2 背景介绍

我们大致介绍一下，说的是『水深火热』的大米国，在旧金山这个地方，一度犯罪率还挺高的，然后很多人都经历过大到暴力案件，小到东西被偷，车被划的事情。当地警方也是努力地去总结和想办法降低犯罪率，一个挑战是在给出犯罪的地点和时间的之后，要第一时间确定这可能是一个什么样的犯罪类型，以确定警力等等。后来干脆一不做二不休，直接把12年内旧金山城内的犯罪报告都丢带Kaggle上，说『大家折腾折腾吧，看看谁能帮忙第一时间预测一下犯罪类型』。犯罪报告里面包括日期，描述，星期几，所属警区，处理结果，地址，GPS定位等信息。当然，分类问题有很多分类器可以选择，我们既然刚讲过朴素贝叶斯，刚好就拿来练练手好了。

7.3 数据一瞥

数据可以在Kaggle比赛数据页面下载到，大家也可以在博主提供的百度网盘地址中下载到。我们依旧用pandas载入数据，先看看数据内容。

import pandas as pd
import numpy as np
 
#用pandas载入csv训练数据，并解析第一列为日期格式
train=pd.read_csv('/Users/Hanxiaoyang/sf_crime_data/train.csv', parse_dates = ['Dates'])
test=pd.read_csv('/Users/Hanxiaoyang/sf_crime_data/test.csv', parse_dates = ['Dates'])
train

得到如下的结果：

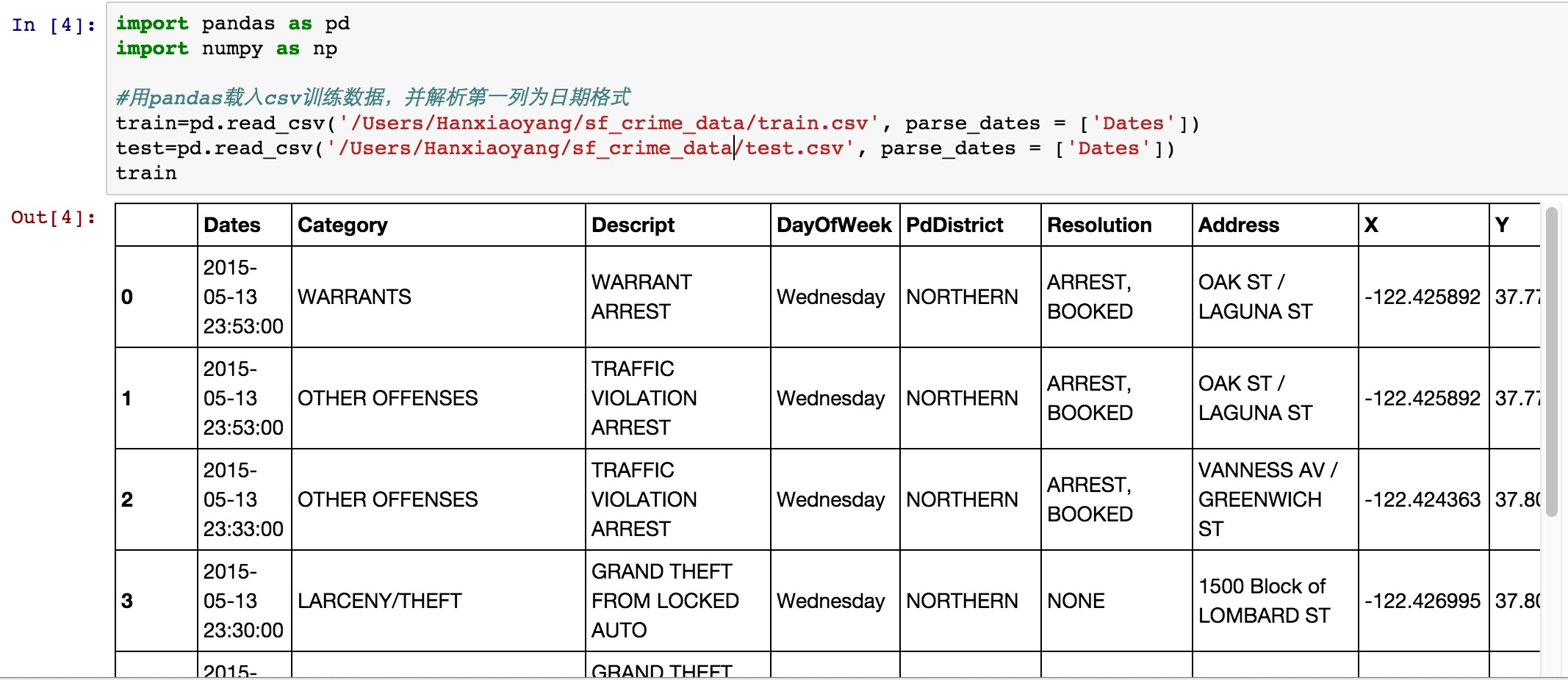
我们依次解释一下每一列的含义：

• Date: 日期
• Category: 犯罪类型，比如 Larceny/盗窃罪 等.
• Descript: 对于犯罪更详细的描述
• DayOfWeek: 星期几
• PdDistrict: 所属警区
• Resolution: 处理结果，比如说『逮捕』『逃了』
• Address: 发生街区位置
• X and Y: GPS坐标

train.csv中的数据时间跨度为12年，包含了90w+的记录。另外，这部分数据，大家从上图上也可以看出来，大部分都是『类别』型，比如犯罪类型，比如星期几。

7.4 特征预处理

上述数据中类别和文本型非常多，我们要进行特征预处理，对于特征预处理的部分，我们在前面的博文机器学习系列(3)_逻辑回归应用之Kaggle泰坦尼克之灾和机器学习系列(6)_从白富美相亲看特征预处理与选择(下)都有较细的介绍。对于类别特征，我们用最常见的因子化操作将其转成数值型，比如我们把犯罪类型用因子化进行encode，也就是说生成如下的向量：

星期一/Monday = 1,0,0,0,...
星期二/Tuesday = 0,1,0,0,...
星期三/Wednesday = 0,0,1,0,...
...

我们之前也提到过，用pandas的get_dummies()可以直接拿到这样的一个二值化的01向量。Pandas里面还有一个很有用的方法LabelEncoder可以用于对类别编号。对于已有的数据特征，我们打算做下面的粗略变换：

• 用LabelEncoder对犯罪类型做编号；
• 处理时间，在我看来，也许犯罪发生的时间点(小时)是非常重要的，因此我们会用Pandas把这部分数据抽出来；
• 对街区，星期几，时间点用get_dummies()因子化；
• 做一些组合特征，比如把上述三个feature拼在一起，再因子化一下；

具体的数据和特征处理如下：

import pandas as pd
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn import preprocessing

#用LabelEncoder对不同的犯罪类型编号
leCrime = preprocessing.LabelEncoder()
crime = leCrime.fit_transform(train.Category)
 
#因子化星期几，街区，小时等特征
days = pd.get_dummies(train.DayOfWeek)
district = pd.get_dummies(train.PdDistrict)
hour = train.Dates.dt.hour
hour = pd.get_dummies(hour) 
 
#组合特征
trainData = pd.concat([hour, days, district], axis=1)
trainData['crime']=crime
 
#对于测试数据做同样的处理
days = pd.get_dummies(test.DayOfWeek)
district = pd.get_dummies(test.PdDistrict)
 
hour = test.Dates.dt.hour
hour = pd.get_dummies(hour) 

testData = pd.concat([hour, days, district], axis=1)
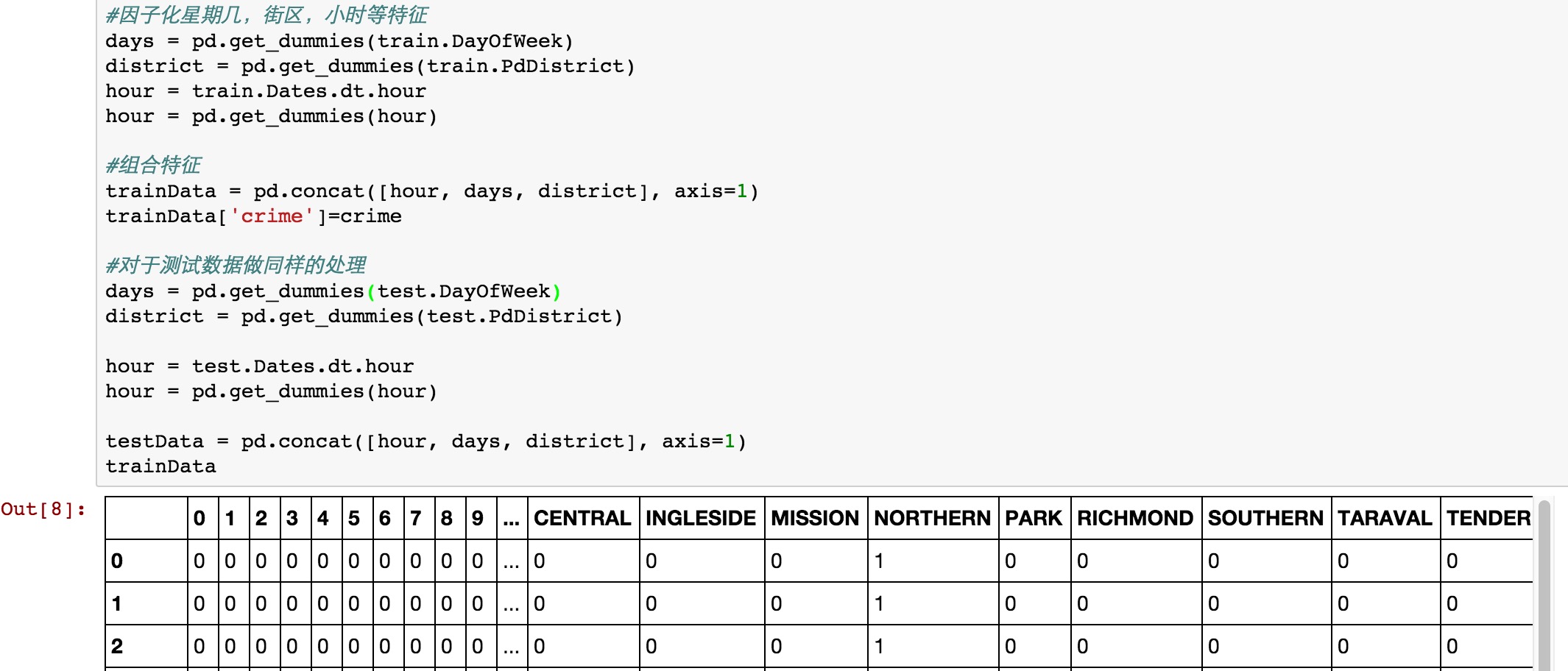
trainData

然后可以看到特征处理后的数据如下所示：

7.5 朴素贝叶斯 VS 逻辑回归

拿到初步的特征了，下一步就可以开始建模了。

因为之前的博客机器学习系列(1)_逻辑回归初步，机器学习系列(2)_从初等数学视角解读逻辑回归，机器学习系列(3)_逻辑回归应用之Kaggle泰坦尼克之灾中提到过逻辑回归这种分类算法，我们这里打算一并拿来建模，做个比较。
还需要提到的一点是，大家参加Kaggle的比赛，一定要注意最后排名和评定好坏用的标准，比如说在现在这个多分类问题中，Kaggle的评定标准并不是precision，而是multi-class log_loss，这个值越小，表示最后的效果越好。

我们可以快速地筛出一部分重要的特征，搭建一个baseline系统，再考虑步步优化。比如我们这里简单一点，就只取星期几和街区作为分类器输入特征，我们用scikit-learn中的train_test_split函数拿到训练集和交叉验证集，用朴素贝叶斯和逻辑回归都建立模型，对比一下它们的表现：

ffrom sklearn.cross_validation import train_test_split
from sklearn import preprocessing
from sklearn.metrics import log_loss
from sklearn.naive_bayes import BernoulliNB
from sklearn.linear_model import LogisticRegression
import time

# 只取星期几和街区作为分类器输入特征
features = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday', 'BAYVIEW', 'CENTRAL', 'INGLESIDE', 'MISSION',
 'NORTHERN', 'PARK', 'RICHMOND', 'SOUTHERN', 'TARAVAL', 'TENDERLOIN']

# 分割训练集(3/5)和测试集(2/5)
training, validation = train_test_split(trainData, train_size=.60)

# 朴素贝叶斯建模，计算log_loss
model = BernoulliNB()
nbStart = time.time()
model.fit(training[features], training['crime'])
nbCostTime = time.time() - nbStart
predicted = np.array(model.predict_proba(validation[features]))
print NLP系列_用朴素贝叶斯进行文本分类(上)

 NLP实战系列朴素贝叶斯文本分类实战
 第10天：NLP补充——朴素贝叶斯(Naive-Bayes)
 02-NLP-02-朴素贝叶斯
 实战：朴素贝叶斯对文档进行分类
 NLP经典分类模型朴素贝叶斯解读