什么是凸函数及如何判断一个函数是否是凸函数

Posted 2020-11-24 技术研究与问题解决

一、什么是凸函数

　对于一元函数f(xf(x)，如果对于任意tϵ[0,1]tϵ[0,1]均满足：f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2)f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2)，则称f(x)f(x)为凸函数(convex function)

　如果对于任意tϵ(0,1)tϵ(0,1)均满足：f(tx1+(1−t)x2)<tf(x1)+(1−t)f(x2)f(tx1+(1−t)x2)<tf(x1)+(1−t)f(x2)，则称f(x)f(x)为严格凸函数(convex function)

　我们可以从几何上直观地理解凸函数的特点，凸函数的割线在函数曲线的上方，如图1所示：

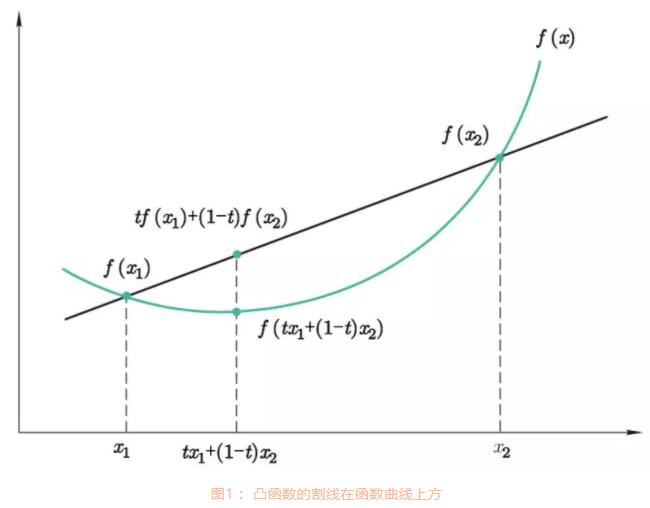
　上面的公式，完全可以推广到多元函数。在数据科学的模型求解中，如果优化的目标函数是凸函数，则局部极小值就是全局最小值。这也意味着我们求得的模型是全局最优的，不会陷入到局部最优值。例如支持向量机的目标函数||w||2/2||w||2/2就是一个凸函数。

 

二、如何来判断一个函数是否是凸函数呢？

　对于一元函数f(x)f(x)，我们可以通过其二阶导数f′′(x)f″(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0f″(x)≥0 ，则f(x)f(x)是凸函数

　对于多元函数f(X)f(X)，我们可以通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是f(X)f(X)凸函数

 

三、Jensen不等式

　对于凸函数，我们可以推广出一个重要的不等式，即Jensen不等式。如果 f 是凸函数，X是随机变量，那么f(E(X))≤E(f(X))f(E(X))≤E(f(X))，上式就是Jensen不等式的一般形式

　我们还可以看它的另一种描述。假设有 n 个样本{x1,x2,...,xn}{x1,x2,...,xn}和对应的权重{α1,α2,...,αn}{α1,α2,...,αn}，权重满足ai⩾0,∑αi=1ai⩾0,∑αi=1，对于凸函数 f，以下不等式成立：

f(∑ni=1αixi)≤∑ni=1αif(xi)f(∑i=1nαixi)≤∑i=1nαif(xi)