图论(2-sat):HDU 4421 Bit Magic
Posted 既然选择了远方,便只顾风雨兼程
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图论(2-sat):HDU 4421 Bit Magic相关的知识,希望对你有一定的参考价值。
Bit Magic
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3040 Accepted Submission(s): 871
Problem Description
Yesterday, my teacher taught me about bit operators: and
(&), or (|), xor (^). I generated a number table a[N], and wrote a
program to calculate the matrix table b[N][N] using three kinds of bit
operator. I thought my achievement would get teacher‘s attention.
The key function is the code showed below.
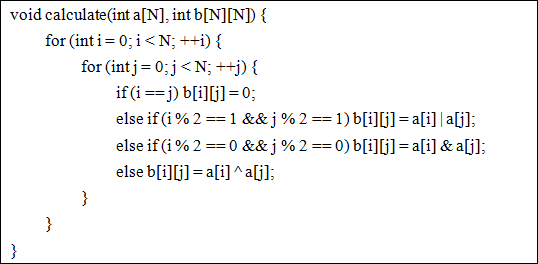
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
The key function is the code showed below.
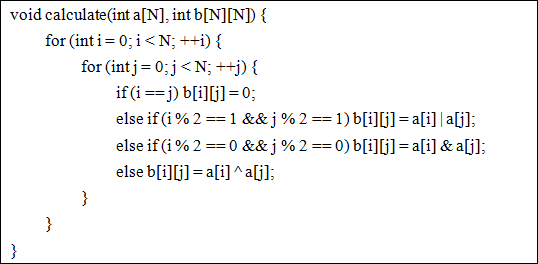
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
Input
There are multiple test cases.
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
Output
For each test case, output "YES" if corresponding number table a[N] exists; otherwise output "NO".
Sample Input
2
0 4
4 0
3
0 1 24
1 0 86
24 86 0
Sample Output
YES
NO
注意数组要开大。
貌似并查集也可以做。
1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 using namespace std; 5 const int maxn=1010; 6 const int maxm=800010; 7 int n,cnt,fir[maxn],to[maxm*2],nxt[maxm*2]; 8 int tot,scnt,ID[maxn],low[maxn],scc[maxn]; 9 10 int min(int a,int b){ 11 return a<b?a:b; 12 } 13 14 void addedge(int a,int b){ 15 nxt[++cnt]=fir[a]; 16 fir[a]=cnt; 17 to[cnt]=b; 18 } 19 20 bool Inst[maxn]; 21 int st[maxn],top; 22 void Tarjan(int x){ 23 low[x]=ID[x]=++tot; 24 st[++top]=x;Inst[x]=true; 25 for(int i=fir[x];i;i=nxt[i]) 26 if(!ID[to[i]]){ 27 Tarjan(to[i]); 28 low[x]=min(low[x],low[to[i]]); 29 } 30 else if(Inst[to[i]]) 31 low[x]=min(low[x],ID[to[i]]); 32 if(low[x]==ID[x]){ 33 ++scnt; 34 while(true){ 35 int y=st[top--]; 36 scc[y]=scnt; 37 Inst[y]=false; 38 if(x==y)break; 39 } 40 } 41 } 42 43 bool Check(){ 44 for(int i=0;i<n*2;i++) 45 if(!ID[i])Tarjan(i); 46 for(int i=0;i<n;i++) 47 if(scc[i*2]==scc[i*2+1]) 48 return false; 49 return true; 50 } 51 52 int b[510][510]; 53 void Init(){ 54 memset(fir,0,sizeof(fir)); 55 memset(scc,0,sizeof(scc)); 56 memset(ID,0,sizeof(ID)); 57 cnt=tot=scnt=0; 58 } 59 60 bool Judge(){ 61 for(int t=0;t<=29;t++){ 62 Init(); 63 for(int i=0;i<n;i++){ 64 for(int j=0;j<n;j++){ 65 if(i==j){if(b[i][j])return false;continue;} 66 else if((i&1)&&(j&1)){ 67 if(b[i][j]&(1<<t)){ 68 addedge(i*2,j*2+1); 69 addedge(j*2,i*2+1); 70 } 71 else{ 72 addedge(i*2+1,i*2);//这两句并不影响答案,有谁知道为啥 73 addedge(j*2+1,j*2);// 74 addedge(i*2,j*2); 75 addedge(j*2,i*2); 76 } 77 } 78 else if(!((i&1)||(j&1))){ 79 if(b[i][j]&(1<<t)){ 80 addedge(i*2,i*2+1); 81 addedge(j*2,j*2+1); 82 addedge(i*2+1,j*2+1); 83 addedge(j*2+1,i*2+1); 84 } 85 else{ 86 addedge(i*2+1,j*2); 87 addedge(j*2+1,i*2); 88 } 89 } 90 else{ 91 if(b[i][j]&(1<<t)){ 92 addedge(i*2+1,j*2); 93 addedge(j*2+1,i*2); 94 addedge(i*2,j*2+1); 95 addedge(j*2,i*2+1); 96 } 97 else{ 98 addedge(i*2,j*2); 99 addedge(j*2,i*2); 100 addedge(i*2+1,j*2+1); 101 addedge(j*2+1,i*2+1); 102 } 103 } 104 } 105 } 106 if(!Check()) 107 return false; 108 } 109 return true; 110 } 111 112 int main(){ 113 while(scanf("%d",&n)!=EOF){ 114 for(int i=0;i<n;i++) 115 for(int j=0;j<n;j++) 116 scanf("%d",&b[i][j]); 117 if(Judge()) 118 printf("YES\n"); 119 else 120 printf("NO\n"); 121 } 122 return 0; 123 }
以上是关于图论(2-sat):HDU 4421 Bit Magic的主要内容,如果未能解决你的问题,请参考以下文章