动态规划 Dynamic Programming
Posted ooon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划 Dynamic Programming相关的知识,希望对你有一定的参考价值。
1. Longest Substring Without Repeating Characters
思路:需要 hashmap 辅助保存各个字符的位置,且随时更新最新位置
若第 i 个位置的字符 c 出现过,则 dp[i] = min(map.get(c)-i,dp[i+1]+1)
若没出现则 dp[i] = dp[i+1] + 1;

public int lengthOfLongestSubstring(String s) {
if (s == null || s.length() == 0) return 0;
Map<Character, Integer> m = new HashMap<Character, Integer>();
int[] dp = new int[s.length()];
dp[s.length() - 1] = 1;
int max = 1; // 初始化dp 数组 与 返回值
m.put(s.charAt(s.length() - 1), s.length() - 1); // 初始化 map
for (int i = s.length() - 2; i >= 0; i--) {
if (m.containsKey(s.charAt(i)))
// 这里要取比较小的一个,避免出现 abbbba 这种情况,虽然间隔大,但是中间都是重复的
dp[i] = Math.min(m.get(s.charAt(i)) - i, dp[i+1]+1);
else
dp[i] = dp[i + 1] + 1;
max = max > dp[i] ? max : dp[i];
m.put(s.charAt(i), i); // 更新位置
}
return max;
}
2. Longest Valid Parentheses
For "(()", the longest valid parentheses substring is "()", which has length = 2.
Another example is ")()())", where the longest valid parentheses substring is "()()", which has length = 4.
题目大意:找到最长的合法括号序列 ,两种形式的 "()()" 与 "((()))" 都是合法的。
思路: 若 i == \')\' 设置 dp[i] = 0 即可;
若 i == \'(\' ,不仅考虑 r = i+1 ; s[r]=\')\' 然后加上 dp[r+1]. 因为还有 "(())" 这种情况
应该考虑 r = i + dp[i+1] + 1; 然后在考虑 dp[r+1] ;这样会考虑到 "(())" 这种情况

public int longestValidParentheses(String s) {
if (s == null || s.length() < 2) return 0;
int max = 0; // 弄个最大值
int []dp = new int[s.length()];
dp[s.length() - 1] =0;
for(int i = s.length() - 2 ; i >= 0 ; -- i){
if(s.charAt(i) == \'(\'){
int ri = i + dp[i+1] + 1;
if(ri < s.length() && s.charAt(ri) == \')\'){
dp[i] = dp[ri] + dp[i+1] + 2;
if(ri + 1 < s.length()-1) dp[i] += dp[ri+ 1];
}
//else dp[i] ==0 可以省略,因为本来就 = 0
}
max = max > dp[i] ? max : dp[i];
}
return max;
}
3. 最长公共子串(Longest Common Substirng)
子串是串的一个连续的部分。
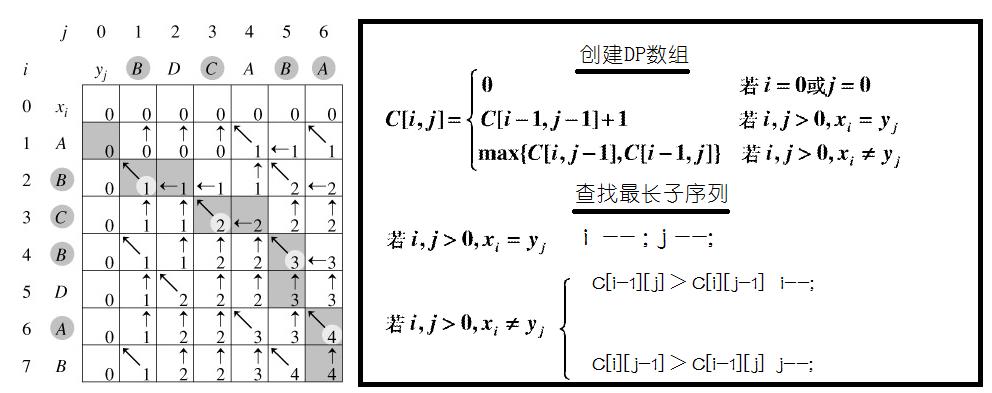
4. 最长公共子序列(Longest Common Sequence)
而从序列中去掉任意的元素而获得新的序列,最长子序列则可以不必连续。

//求 最长子序列的长度
public static void LongestCommonSequence(String s1 , String s2){
int m = s1.length();
int n = s2.length();
if(m == 0 || n == 0) return;
int dp[][] = new int[m+1][n+1];
//构建
for(int i = 1 ; i <= m; i ++){
for(int j = 1; j <= n; j ++){
if(s1.charAt(i-1)== s2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1]+1;
}else
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
//查找
String LCS = ""; int i = m,j = n;
while (i >= 1 && j >= 1) {
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
char c = s1.charAt(i - 1);
LCS = c + LCS;
i--;
j--;
} else if (dp[i][j - 1] > dp[i - 1][j]) {
j--;
} else {
i--;
}
}
System.out.println(LCS);// 打印
}
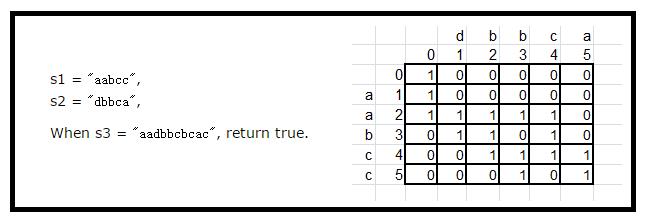

//类似于 LCS 的动态规划 public boolean isInterleave(String s1, String s2, String s3) { int m = s1.length(),n = s2.length(); if(m + n != s3.length()) return false; //横向放 s1 ,纵向放 s2 boolean dp[][] = new boolean [m+1][n+1]; dp[0][0] = true; // 把左上角元素置 true ,因为有 S1=""、 S2="" 、S3="" 的情况 for(int i = 1 ; i < dp.length; i ++){ if(s1.charAt(i-1) == s3.charAt(i-1)) dp[i][0] = true; else break; } for(int j = 1 ; j < dp[0].length; j ++){ if(s2.charAt(j-1) == s3.charAt(j-1)) dp[0][j] = true; else break; } for(int i = 0 ; i < m ; i ++){ for(int j = 0 ; j < n ; j ++){ if(s2.charAt(j) == s3.charAt(i+j+1) && dp[i+1][j] == true){dp[i+1][j+1] = true;} if(s1.charAt(i) == s3.charAt(i+j+1) && dp[i][j+1] == true){dp[i+1][j+1] = true;} } } return dp[m][n] == true ; }
6. Maximum Subarray (leetcode)
找到和最大的连续子序列,比如对于序列 [−2,1,−3,4,−1,2,1,−5,4],和最大的连续子序列为[4,−1,2,1] ,和的最大值= 6.

public int maxSubArray(int[] nums) { if(nums == null || nums.length == 0) return 0; int dp[] = new int[nums.length];// 动态规划数组 dp[dp.length-1] = nums[nums.length - 1]; int ret = nums[nums.length - 1];// 待返回结果 for(int i = nums.length - 2; i >= 0 ; i --){ if(nums[i] + dp[i+1] <= nums[i]){ dp[i] = nums[i]; }else{ dp[i] = dp[i+1] + nums[i]; } ret = Math.max(dp[i],ret); } return ret; }
7. 蘑菇阵(牛客网)
现在有两个好友A和B,住在一片长有蘑菇的由n*m个方格组成的草地,A在(1,1),B在(n,m)。现在A想要拜访B,由于她只想去B的家,所以每次她只会走(i,j+1)或(i+1,j)这样的路线,在草地上有k个蘑菇种在格子里(多个蘑菇可能在同一方格),问:A如果每一步随机选择的话(若她在边界上,则只有一种选择),那么她不碰到蘑菇走到B的家的概率是多少?
第一行N,M,K(2 ≤ N,M ≤ 20, k ≤ 100),N,M为草地大小,接下来K行,每行两个整数x,y,代表(x,y)处有一个蘑菇。
思路:二维数组的DP,起始点概率为 1 ;
对于内部节点,当前点向右边走的概率为 0.5 ,下边走的概率为 0.5 ;
注意右边界与下边界,边界节点只有一个方向。

import java.util.Scanner; public class Main{ public static void main(String[]args){ Scanner sc = new Scanner(System.in); while(sc.hasNext()){ int n = sc.nextInt(); int m = sc.nextInt(); int k = sc.nextInt(); double[][] dp = new double[n+1][m+1]; // 地图 for(int i = 0 ; i < k ; i ++) dp[sc.nextInt()][sc.nextInt()] = 1; // i -> col ; j -> row for(int i = 1 ; i <= n ; i ++){ for(int j = 1 ; j <= m ; j ++){ //走到蘑菇上了,转移概率置 0 . if(dp[i][j] == 1){ dp[i][j] = 0; // 起始位置 }else if(i == 1 && j == 1){ dp[i][j] = 1; // 最后一个元素等于上左概率相加 }else if(i == n && j == m){ dp[i][j] = dp[i-1][j] + dp[i][j-1]; // 最后一列只能下移 }else if(j == m){ dp[i][j] = dp[i-1][j] + 0.5 * dp[i][j-1]; // 最后一行只能右移 }else if(i == n){ dp[i][j] = 0.5 * dp[i-1][j] + dp[i][j-1]; // 内部元素一半几率来自上,一半几率来自左 }else{ dp[i][j] = 0.5 * dp[i-1][j] + 0.5 * dp[i][j-1]; } } } System.out.println(String.format("%.2f", 1.0 * dp[n][m])); } } }
8.Longest Increasing Path in a Matrix(leetcode)
nums = [[9,9,4], [6,6,8], [2,1,1]]
Return4The longest increasing path is[1, 2, 6, 9].
[8, 6, 4, 3] [1, 2, 3, 4]
[2, 9, 2, 5] [3, 1, 4, 3]
[7, 4, 1, 6] [2, 3, 5, 2]
[8, 2, 4, 7] [1, 4, 2, 1]

//本题目就是结合 DFS 的DP public int longestIncreasingPath(int[][] matrix) { if(matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0; int ret = 0; int m = matrix.length, n = matrix[0].length; int[][] dp = new int[m][n]; for(int i = 0 ; i < m ; i ++){ for(int j = 0 ; j< n ; j ++){ int len = dfs(matrix, i, j, m, n, dp); ret = Math.max(ret, len); } } return ret; } public int dfs(int[][] matrix, int i,int j, int m,int n,int[][] dp){ if(dp[i][j] != 0) return dp[i][j]; // 这一步比较关键,用到了 DP数组 if(i < 0 || i > m-1 || j < 0 || j > n-1) return 0; int max = 0; //分别从上下左右搜索变大的方向. if(i > 0 && matrix[i][j] < matrix[i-1][j]){//上 int up = dfs(matrix, i-1, j, m, n, dp); max = Math.max(max, up); } if(i < m-1 && matrix[i][j] < matrix[i+1][j]){//下 int down = dfs(matrix, i+1, j, m, n, dp); max = Math.max(max, down); } if(j > 0 && matrix[i][j] < matrix[i][j-1]){//左 int left = dfs(matrix, i, j-1, m, n, dp); max = Math.max(max, left); } if(j < n-1 && matrix[i][j] < matrix[i][j+1]){//右 int right= dfs(matrix, i, j+1, m, n, dp); max = Math.max(max, right); } dp[i][j] = max + 1; // + 1 表示加上自身的操作 return dp[i][j]; }
9. Combination Sum IV (leetcode)
思路:dp[i]表示当target为i 时,有多少种组合。
状态转移方程:dp[i]=$\\sum_{j}$dp[i-nums[j]] ;
时间复杂度 $O(n^2)$

public int combinationSum4(int[] nums, int target) { int[] dp = new int[target + 1]; for(int i = 1 ; i < dp.length ; i ++){ for(int num : nums){ if( num > i ) continue; else if(num == i) dp[i] += 1; else dp[i] += dp[i - num]; } } return dp[target]; }
10. 0-1 背包问题
给定质量 m ,怎么偷走最多的物品来达到赚最多的钱
思路:dp 做,用 dp[i][j]表示前 i个物品,装到容量为j的背包的最大价值
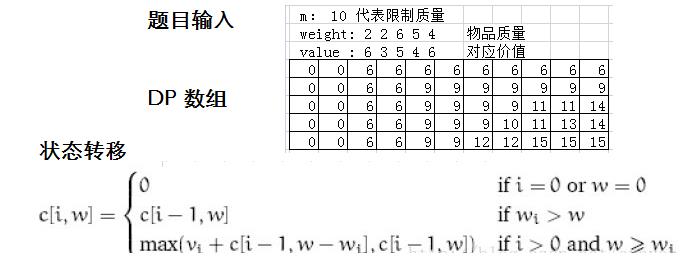
dp[i][j]表示放入前 i 件物品且背包容量为 j 时的最大价值。
当只能放入第一件物品即 i=0 时:若背包容量 j < weight[0],物品不能够被放入背包, 若 j >= weight[0] 时,物品可以放入背包,此时 dp[0][j] = value[0]。
当可以放入前2件物品即 i=1 时,我们需要进行这样的处理:若 j<w[1] 时,说明第 2 件物品不能被放入背包内,此时背包的最大价值为背包中只放入第一件物品的最大价值,即 dp[1][j] =d p[0][j], 若 j >= weight[1] 时,假设此时背包容量 j = 8 ,第二件物品可以被放入背包内,那么便会出现两种情况:
1)将第二件物品放入背包,那么背包中物品的最大价值是多少呢?因为第二件物品重量为 weight[1]=2 ,在将第二件物品放入背包之前,背包的容量应为 j-weight[1] = 8-2 = 6,此时背包的最大价值是 dp[0][6] ,因此若将第二件物品放入背包,其背包的最大价值:
dp[1][j] = dp[0][j-weight[1]] + value[1]
2)不将第二件物品放入背包,那么此时背包中物品的最大价值依然为只放入第一件物品时背包的最大价值,即 dp[1][j] = dp[0][j];
3)选取1)、2)中价值的较大者作为 i=1,j=8 时背包中的最大价值。
i = 2,3,4 时的分析同上,直到背包的容量为10,此时 dp[4][10] 即为背包中物品的最大价值。

import java.util.Arrays; import java.util.Scanner; public class Main{ //0-1 背包问题 public static void main(String args[]){ Scanner sc = new Scanner(System.in); while(sc.hasNext()){// 0-1 背包 String[] arg = sc.nextLine().split(" "); int m = Integer.parseInt(arg[0]); // 总质量不能超过 m int n = Integer.parseInt(arg[1]); // 物品总数为 n int[] weight = new int[n]; int[] value = new int[n]; String[] w = sc.nextLine().split(" "); String[] v = sc.nextLine().split(" "); for(int i = 0 ; i < n ; i ++){ weight[i] = Integer.parseInt(w[i]); value [i] = Integer.parseInt(v[i]); } //dp[i][j]表示前 i个物品,装到容量为j的背包的最大价值 int[][] dp = new int[n][m + 1]; for(int i = 0 ; i <= m ; i ++) //第 0 行初始化 if( i >= weight[0]) dp[0][i] = value[0]; //计算状态转移数组 for(int i = 1; i < n; i ++) { for(int j = 1; j <= m; j ++) { if (j >= weight[i]) //dp[i - 1][j - weight[i]] 上一次不加当前物品的最大利润 dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); // j < weight[i] else dp[i][j] = dp[i - 1][j]; } } int ret = dp[n - 1][m]; System.out.println(String.format("%.1f", ret)); } sc.close(); } }
11. Distinct Subsequences (leetcode)
// dp[i][j]表示:T的前j个字符在S的前i个字符中的合法序列数。
思路:1) 假设S[i] != T[j] ,则 dp[i][j]的值跟dp[i-1][j]是一样的,第 i 个字符加入没有任何用处,不考虑当前这个字符,延续上一次的结果。
2) 假设S[i] == T[j],那么当前这个字母即可以保留也可以抛弃,所以变换方法等于保留这个字母的变换方法加上不用这个字母的变换方法。
3) 上一次的结果为 dp[i-1][j] , 之前的变换结果为 dp[i-1][j-1] ,注意 dp[i][0] = 1 代表任意串转为空串只需做一次变换
例如: 对于 S = rabbbit 与 T = rabit 中的 DP 数组如下:
r a b i t
[ 1, 0, 0, 0, 0, 0]
r [1, 1, 0, 0, 0, 0]
a [1, 1, 1, 0, 0, 0]
b [1, 1, 1, 1, 0, 0]
b [1, 1, 1, 2, 0, 0]
b [1, 1, 1, 3, 0, 0]
i [1, 1, 1, 3, 3, 0]
t [1, 1, 1, 3, 3, 3]

// 序列 T 可以有以多少种不同的方式作为 S 的子序列 public int numDistinct(String s, String t) { if(s == null || t == null) return 0; int m = s.length(), n = t.length(); int[][] dp = new int[m + 1][n + 1]; dp[0][0] = 1; //任何一个串变为空串都只有一种方式 for(int i = 0 ; i <= m ; i ++) dp[i][0] = 1; for(int i = 1 ; i <= m ; i ++){ for(int j = 1 ; j <= n ; j ++){ if(s.charAt(i-1) == t.charAt(j-1)){ dp[i][j] = dp[i-1][j-1] + dp[i-1][j]; }else{ dp[i][j] = dp[i-1][j]; } } } return dp[m][n]; }
12. 幸运数字
给定 一组数字,[1, 2, ..., i, ..., T] ,每个数字的范围是 1 <= i <= n ,计算每个数字 i 的在范围 [1,i] 中幸运数字量。
思路:这个题因为对于一组数字,比如说 1000,1001,两个数字得到的值可能回事一样的,但需要计算两遍,所以数组里每个数字都重新计算一遍的话会超时,需要用一个数组保存一下之前的信息:

import java.util.*; public class Main { public static void main(String[] args){ int size = 1000001; // 题目给的最大值范围 int dp[] = new int [size]; dp(dp); // dp[i] 表示 [1,i]里的幸运数的总数 Scanner sc = new Scanner(System.in); while(sc.hasNext()){ int T = Integer.parseInt(sc.nextLine()); int [] nums = new int[T]; for(int i = 0 ; i < T ; i ++){ int n = Integer.parseInt(sc.nextLine()); nums[i] = dp[n]; } for(int i = 0 ; i < nums.length ; i ++){ System.out.println(nums[i]); } } } public static void dp(int[] dp){ int count = 0; for(int i = 1; i < dp.length ; i ++){ int cur = i; int sum = 0, binsum = 0; while( cur > 0){ sum += cur % 10; cur /= 10; } String binstr = Integer.toBinaryString(i); for(char c : binstr.toCharArray()){ binsum +=c - \'0\'; } if(sum == binsum) count ++; dp[i] = count; } } }
13. Edit Distance (leetcode)
思路: 动态规划, dp[i][j] 表示字符串 word1 的前 i 个字符与字
以上是关于动态规划 Dynamic Programming的主要内容,如果未能解决你的问题,请参考以下文章
