leetcode315 计算右侧小于当前元素的个数

Posted 2020-11-22 Joel_Wang

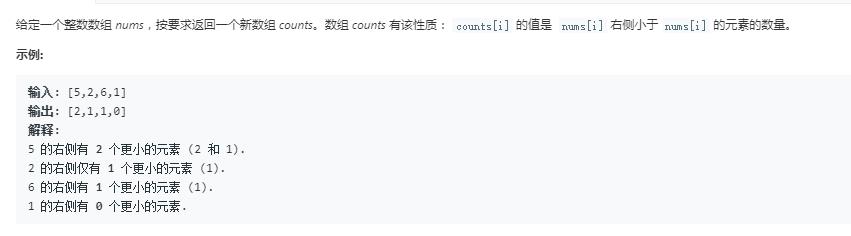
1. 采用归并排序计算逆序数组对的方法来计算右侧更小的元素 time O(nlogn)；

计算逆序对可以采用两种思路：

　　a. 在左有序数组元素出列时计算右侧比该元素小的数字的数目为 cnt=r-mid-1; 右有序数组出列完成后cnt=end-mid;

　　b. 在右有序数组元素出列时计算左侧比该元素大的数字的数目为 cnt=mid-l+1; 左有序数组出列完成后cnt=0;

 思路参考from https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/solution/gui-bing-pai-xu-suo-yin-shu-zu-python-dai-ma-java-/

但是只有python 和java, 补充C++代码；

 C++ code：

class Solution {
public:
    void merge(vector<int>& nums, vector<int>& indexs,vector<int>& counts,int start, int mid, int end){
        //在左有序数组出列时计算右有序数组中比当前数字小的
        vector<int> tmps;//存储临时的index;
        int l=start;
        int r=mid+1;
        while(l<=mid && r<=end){
            if(nums[indexs[l]]<=nums[indexs[r]]){
                tmps.push_back(indexs[l]);
                counts[indexs[l]]+=r-mid-1;
                l++;
            }else{
                tmps.push_back(indexs[r]);
                r++;
            }
        }
        while(l<=mid){
            tmps.push_back(indexs[l]);
            counts[indexs[l]]+=end-mid;
            l++;
        }
        while(r<=end){
            tmps.push_back(indexs[r]);
            r++;
        }
        for(int i=0;i<tmps.size();i++){
            indexs[start+i]=tmps[i];
        }
    }
    void mergesort(vector<int>& nums, vector<int>& indexs, vector<int>& counts,int start, int end){
        if(start>=end) return;
        int mid=start+(end-start)/2;
        mergesort(nums,indexs,counts,start,mid);
        mergesort(nums,indexs,counts,mid+1,end);
        if(nums[indexs[mid]]>nums[indexs[mid+1]])
            merge(nums,indexs,counts,start,mid,end);
    }
    vector<int> countSmaller(vector<int>& nums) {
        //归并排序计算 time nlogn
        int len=nums.size();
        vector<int> counts(len,0);
        vector<int> indexs(len,0);
        for(int i=0;i<len;i++){
            indexs[i]=i;
        }
        mergesort(nums,indexs,counts,0,len-1);
        return counts;
    }
};

 可以采用一个全局的tmps临时数组而不是每次都中转；然后合并l<mid 与 (nums[indexs[l]]<=nums[indexs[r]])，简化代码如下：

class Solution {
public:
    void merge(vector<int>& nums, vector<int>& indexs, vector<int>& counts, vector<int>& tmps, int start, int mid, int end){
        int l=start;
        int r=mid+1;
        for(int i=start;i<=end;i++){
            if(r>end || ((l<=mid)&&(nums[indexs[l]]<=nums[indexs[r]]))){
                tmps[i]=indexs[l];
                counts[indexs[l]]+=r-mid-1;
                l++;
            }else{
                tmps[i]=indexs[r++];
            }
        }
        for(int i=start;i<=end;i++){
            indexs[i]=tmps[i];
        }
    }
    void mergesort(vector<int>& nums, vector<int>& indexs, vector<int>& counts, vector<int>& tmps, int start, int end){
        if(start>=end) return;
        int mid=start+(end-start)/2;
        mergesort(nums,indexs,counts,tmps,start,mid);
        mergesort(nums,indexs,counts,tmps,mid+1,end);
        merge(nums,indexs,counts,tmps,start,mid,end);
    }
    vector<int> countSmaller(vector<int>& nums) {
        //可以借鉴利用归并排序统计逆序对数，
        int len=nums.size();
        if(len==0) return {};
        
        vector<int> indexs,counts,tmps;
        for(int i=0;i<len;i++){
            indexs.push_back(i),counts.push_back(0),tmps.push_back(0);
        }
        mergesort(nums,indexs,counts,tmps,0,len-1);
        return counts;
    }
};

 2. 对O(n2)的暴力搜索进行改进：

倒序遍历，用一个数组sorted_nums记录当前元素右边的元素排序后的结果，每次用二分查找寻找新元素插入位置，并且得到right为counts的结果；

time O(n（n+logn）)但是要比归并排序慢十倍，是因为vector插入元素的关系？

C++ code：

class Solution {
public:
    vector<int> countSmaller(vector<int>& nums) {
        //暴力搜索，但是是从末尾计算，且将计算过的数排序存储，便于使用二分查找；
        vector<int> sorted_nums, res;
        for(int i=nums.size()-1;i>=0;i--){
            int left=0;
            int right=sorted_nums.size();//这样mid索引不会出界，因为mid总是小于sorted_nums的长度的
　　　　　　　//寻找nums[i]插入的位置，即比nums[i]大得第一个元素的位置；

            while(left<right){
                int mid=left+(right-left)/2;
                if(sorted_nums[mid]>=nums[i]){
                    right=mid;
                }else{
                    left=mid+1;
                }
            }
            res.push_back(right);
            sorted_nums.insert(sorted_nums.begin()+right,nums[i]);
        }
        reverse(res.begin(),res.end());
        return res;
    }
};

 

num  [nʌm]  详细X

基本翻译

abbr. 号码（number）；数字（numeral）

n. (Num)人名；(柬)农

网络释义

nums: 小海豹冲冲冲

private nums: 总条目数

Big Nums: 大数问题