图的遍历：拓扑排序

Posted 2020-06-13

【需要解决的问题】

对一个有向无环图（DAG）拓扑排序。

拓扑排序就是，对图上的点进行排序，使得排在后面的点不能通过一条路径到前面的点。

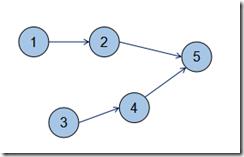
比如下面这个图：

         

 其中一个拓扑排序是1，2，3，4，5；而1，2，5，3，4就不行，因为3能到达5。

因此可以得出：

用一个队列实现，先把入度为0的点放入队列，每次将队首元素加入ans[i…j]中，删除队首元素，并删除该点连接的所有边，于是每次删除一个点都会产生一个新的入度为0的点，再把这个点插入队列，递归即可。

拓扑排序 模板如下：

//复杂度：O（N+M），N为点数，M为边数
//输入：n，vector变量g[] n表示点的个数，g[i][j]表示从点i连出去到点j的边,有g[i][j]=j;
//输出：返回对给定的图，是否能够拓扑排序；L[]用来记录拓扑排序的结果

const int MAXN=100005;

vector<int> g[MAXN];
int degree[MAXN],L[MAXN],n,m;

bool toposort()
{
    memset(degree,0,sizeof(degree));
    for(int i=0;i<n;i++)
        for(int j=0;j<g[i].size();j++)
            degree[g[i][j]]++;
    int tot=0;
    queue<int> que;  //tuposort的实现类似于BFS
    for(int i=0;i<n;i++)
        if(!degree[i])
            que.push(i);
    while(!que.empty())
    {
        int x=que.front();que.pop();
        L[tot++]=x;
        for(int j=0;j<g[x].size();j++)
        {
            int t=g[x][j];
            degree[t]--;
            if(!degree[t])
                que.push(t);
        }
    }
    if(tot==n) return true;
    return false;
}