401 biharmonic deformation
Posted seamanj
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了401 biharmonic deformation相关的知识,希望对你有一定的参考价值。
let us look at the definition of biharmonic deformation first:
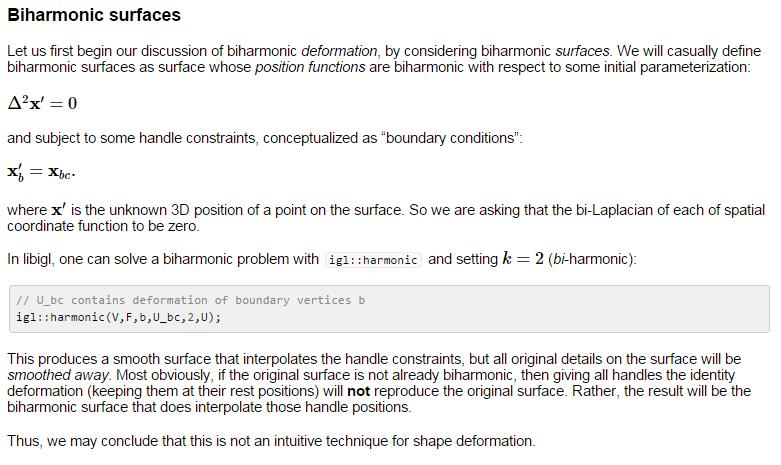
Then take a look at the definition of biharmonic deformation fields

The difference between them is Biharmonic surface works directly with position X directly, however, Biharmonic deformation work with deformation fields(ie. displacements).

Biharmonic functions (whether positions or displacements) are solutions to the bi-Laplace equation, but also minimizers of the “Laplacian energy”, which can be seen from: http://blog.csdn.net/seamanj/article/details/50898781 and alec jacobson's thesis:

Laplacian energy and laplacian gradient energy 在Mixed Finite Elements for Variational Surface Modeling里面有介绍
Dirichlet energy 在laplacian interpolation有用到
the formula 3.21(biharmonic equation) is the case in here, whereas the formula 3.20(harmonic equation) is used for laplacian interpolation which can be seen from: http://blog.csdn.net/seamanj/article/details/51738180
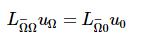
这个式子是最小化Dirichlet energy的, 也就是解harmonic equation. 推导可见Alec jacobson thesis analysis N4
http://blog.csdn.net/seamanj/article/details/50899217#t4
For better understanding the source code of libigl, I firstly would like to cite a equation from the paper "Mixed Finite Elements for Variational Surface Modeling", whose details can be found on "http://blog.csdn.net/seamanj/article/details/51724020"
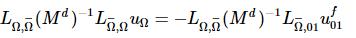 ....................................................(*1)
....................................................(*1)
这个式子是最小化Laplacian energy的, 也就是解biharmonic equation. 推导可见Mixed Finite Elements for Variational Surface Modeling
http://blog.csdn.net/seamanj/article/details/51724020?locationNum=1&fps=1
now, it is time to analyze the source code:
#include <igl/colon.h>
#include <igl/harmonic.h>
#include <igl/readOBJ.h>
#include <igl/readDMAT.h>
#include <igl/viewer/Viewer.h>
#include <algorithm>
#include <iostream>
#include "tutorial_shared_path.h"
double bc_frac = 1.0;
double bc_dir = -0.03;
bool deformation_field = false;
Eigen::MatrixXd V,U,V_bc,U_bc;
Eigen::VectorXd Z;
Eigen::MatrixXi F;
Eigen::VectorXi b;
bool pre_draw(igl::viewer::Viewer & viewer)
{
using namespace Eigen;
// Determine boundary conditions
if(viewer.core.is_animating)
{
bc_frac += bc_dir;
bc_dir *= (bc_frac>=1.0 || bc_frac<=0.0?-1.0:1.0);
}
const MatrixXd U_bc_anim = V_bc+bc_frac*(U_bc-V_bc);// U_bc_anim is the actual postion of each boundary vertex.
if(deformation_field)
{
MatrixXd D;
MatrixXd D_bc = U_bc_anim - V_bc;
igl::harmonic(V,F,b,D_bc,2,D);//biharmonic deformation fields(displacements)
U = V+D;
}else
{
igl::harmonic(V,F,b,U_bc_anim,2,U);// biharmonic surface, this would smooth the surface(i.e. lose the details on the surface)
}
viewer.data.set_vertices(U);
viewer.data.compute_normals();
return false;
}
bool key_down(igl::viewer::Viewer &viewer, unsigned char key, int mods)
{
switch(key)
{
case ' ':
viewer.core.is_animating = !viewer.core.is_animating;
return true;
case 'D':
case 'd':
deformation_field = !deformation_field;
return true;
}
return false;
}
int main(int argc, char *argv[])
{
using namespace Eigen;
using namespace std;
igl::readOBJ(TUTORIAL_SHARED_PATH "/decimated-max.obj",V,F);
U=V;
// S(i) = j: j<0 (vertex i not in handle), j >= 0 (vertex i in handle j)
VectorXi S;
igl::readDMAT(TUTORIAL_SHARED_PATH "/decimated-max-selection.dmat",S);
igl::colon<int>(0,V.rows()-1,b);
b.conservativeResize(stable_partition( b.data(), b.data()+b.size(),
[&S](int i)->bool{return S(i)>=0;})-b.data());//the domain where greater than or equal 0 is in purple denoting the boundary conditions.
// Boundary conditions directly on deformed positions
U_bc.resize(b.size(),V.cols());
V_bc.resize(b.size(),V.cols());
// V_bc represents the original positions of the boundary vertices, wheareas U_bc for the goal positions of them.
for(int bi = 0;bi<b.size();bi++)
{
V_bc.row(bi) = V.row(b(bi));
switch(S(b(bi)))// value in S represents the group order of boundary vertex, of which -1 stands for interior vertex.
{
case 0:
// Don't move handle 0
U_bc.row(bi) = V.row(b(bi));
break;
case 1:
// move handle 1 down
U_bc.row(bi) = V.row(b(bi)) + RowVector3d(0,-50,0);
break;
case 2:
default:
// move other handles forward
U_bc.row(bi) = V.row(b(bi)) + RowVector3d(0,0,-25);
break;
}
}
// Pseudo-color based on selection
MatrixXd C(F.rows(),3);
RowVector3d purple(80.0/255.0,64.0/255.0,255.0/255.0);
RowVector3d gold(255.0/255.0,228.0/255.0,58.0/255.0);
for(int f = 0;f<F.rows();f++)
{
if( S(F(f,0))>=0 && S(F(f,1))>=0 && S(F(f,2))>=0)
{
C.row(f) = purple;
}else
{
C.row(f) = gold;
}
}
// Plot the mesh with pseudocolors
igl::viewer::Viewer viewer;
viewer.data.set_mesh(U, F);
viewer.core.show_lines = false;
viewer.data.set_colors(C);
viewer.core.trackball_angle = Eigen::Quaternionf(sqrt(2.0),0,sqrt(2.0),0);
viewer.core.trackball_angle.normalize();
viewer.callback_pre_draw = &pre_draw;
viewer.callback_key_down = &key_down;
//viewer.core.is_animating = true;
viewer.core.animation_max_fps = 30.;
cout<<
"Press [space] to toggle deformation."<<endl<<
"Press 'd' to toggle between biharmonic surface or displacements."<<endl;
viewer.launch();
}
Next, let us focus on the function igl::hamonic in order to see how it constructs the equation and then relate it with the (*1) formula.
At first, we look into the min_quad_with_fiexed.h file
// This file is part of libigl, a simple c++ geometry processing library.
//
// Copyright (C) 2014 Alec Jacobson <alecjacobson@gmail.com>
//
// This Source Code Form is subject to the terms of the Mozilla Public License
// v. 2.0. If a copy of the MPL was not distributed with this file, You can
// obtain one at http://mozilla.org/MPL/2.0/.
#ifndef IGL_MIN_QUAD_WITH_FIXED_H
#define IGL_MIN_QUAD_WITH_FIXED_H
#include "igl_inline.h"
#define EIGEN_YES_I_KNOW_SPARSE_MODULE_IS_NOT_STABLE_YET
#include <Eigen/Core>
#include <Eigen/Dense>
#include <Eigen/Sparse>
// Bug in unsupported/Eigen/SparseExtra needs iostream first
#include <iostream>
#include <unsupported/Eigen/SparseExtra>
namespace igl
{
template <typename T>
struct min_quad_with_fixed_data;
// Known Bugs: rows of Aeq **should probably** be linearly independent.
// During precomputation, the rows of a Aeq are checked via QR. But in case
// they're not then resulting probably will no longer be sparse: it will be
// slow.
//
// MIN_QUAD_WITH_FIXED Minimize quadratic energy
//
// 0.5*Z'*A*Z + Z'*B + C with
//
// constraints that Z(known) = Y, optionally also subject to the constraints
// Aeq*Z = Beq
//
// Templates:
// T should be a eigen matrix primitive type like int or double
// Inputs:
// A n by n matrix of quadratic coefficients
// known list of indices to known rows in Z
// Y list of fixed values corresponding to known rows in Z
// Aeq m by n list of linear equality constraint coefficients
// pd flag specifying whether A(unknown,unknown) is positive definite
// Outputs:
// data factorization struct with all necessary information to solve
// using min_quad_with_fixed_solve
// Returns true on success, false on error
//
// Benchmark: For a harmonic solve on a mesh with 325K facets, matlab 2.2
// secs, igl/min_quad_with_fixed.h 7.1 secs
//
template <typename T, typename Derivedknown>
IGL_INLINE bool min_quad_with_fixed_precompute(
const Eigen::SparseMatrix<T>& A,
const Eigen::PlainObjectBase<Derivedknown> & known,
const Eigen::SparseMatrix<T>& Aeq,
const bool pd,
min_quad_with_fixed_data<T> & data
);
// Solves a system previously factored using min_quad_with_fixed_precompute
//
// Template:
// T type of sparse matrix (e.g. double)
// DerivedY type of Y (e.g. derived from VectorXd or MatrixXd)
// DerivedZ type of Z (e.g. derived from VectorXd or MatrixXd)
// Inputs:
// data factorization struct with all necessary precomputation to solve
// B n by 1 column of linear coefficients
// Y b by 1 list of constant fixed values
// Beq m by 1 list of linear equality constraint constant values
// Outputs:
// Z n by cols solution
// sol #unknowns+#lagrange by cols solution to linear system
// Returns true on success, false on error
template <
typename T,
typename DerivedB,
typename DerivedY,
typename DerivedBeq,
typename DerivedZ,
typename Derivedsol>
IGL_INLINE bool min_quad_with_fixed_solve(
const min_quad_with_fixed_data<T> & data,
const Eigen::PlainObjectBase<DerivedB> & B,
const Eigen::PlainObjectBase<DerivedY> & Y,
const Eigen::PlainObjectBase<DerivedBeq> & Beq,
Eigen::PlainObjectBase<DerivedZ> & Z,
Eigen::PlainObjectBase<Derivedsol> & sol);
// Wrapper without sol
template <
typename T,
typename DerivedB,
typename DerivedY,
typename DerivedBeq,
typename DerivedZ>
IGL_INLINE bool min_quad_with_fixed_solve(
const min_quad_with_fixed_data<T> & data,
const Eigen::PlainObjectBase<DerivedB> & B,
const Eigen::PlainObjectBase<DerivedY> & Y,
const Eigen::PlainObjectBase<DerivedBeq> & Beq,
Eigen::PlainObjectBase<DerivedZ> & Z);
template <
typename T,
typename Derivedknown,
typename DerivedB,
typename DerivedY,
typename DerivedBeq,
typename DerivedZ>
IGL_INLINE bool min_quad_with_fixed(
const Eigen::SparseMatrix<T>& A,
const Eigen::PlainObjectBase<DerivedB> & B,
const Eigen::PlainObjectBase<Derivedknown> & known,
const Eigen::PlainObjectBase<DerivedY> & Y,
const Eigen::SparseMatrix<T>& Aeq,
const Eigen::PlainObjectBase<DerivedBeq> & Beq,
const bool pd,
Eigen::PlainObjectBase<DerivedZ> & Z);
}
template <typename T>
struct igl::min_quad_with_fixed_data
{
// Size of original system: number of unknowns + number of knowns
int n;
// Whether A(unknown,unknown) is positive definite
bool Auu_pd;
// Whether A(unknown,unknown) is symmetric
bool Auu_sym;
// Indices of known variables
Eigen::VectorXi known;
// Indices of unknown variables
Eigen::VectorXi unknown;
// Indices of lagrange variables
Eigen::VectorXi lagrange;
// Indices of unknown variable followed by Indices of lagrange variables
Eigen::VectorXi unknown_lagrange;
// Matrix multiplied against Y when constructing right hand side
Eigen::SparseMatrix<T> preY;
enum SolverType
{
LLT = 0,
LDLT = 1,
LU = 2,
QR_LLT = 3,
NUM_SOLVER_TYPES = 4
} solver_type;
// Solvers
Eigen::SimplicialLLT <Eigen::SparseMatrix<T > > llt;
Eigen::SimplicialLDLT<Eigen::SparseMatrix<T > > ldlt;
Eigen::SparseLU<Eigen::SparseMatrix<T, Eigen::ColMajor>, Eigen::COLAMDOrdering<int> > lu;
// QR factorization
// Are rows of Aeq linearly independent?
bool Aeq_li;
// Columns of Aeq corresponding to unknowns
int neq;
Eigen::SparseQR<Eigen::SparseMatrix<T>, Eigen::COLAMDOrdering<int> > AeqTQR;
Eigen::SparseMatrix<T> Aeqk;
Eigen::SparseMatrix<T> Aequ;
Eigen::SparseMatrix<T> Auu;
Eigen::SparseMatrix<T> AeqTQ1;
Eigen::SparseMatrix<T> AeqTQ1T;
Eigen::SparseMatrix<T> AeqTQ2;
Eigen::SparseMatrix<T> AeqTQ2T;
Eigen::SparseMatrix<T> AeqTR1;
Eigen::SparseMatrix<T> AeqTR1T;
Eigen::SparseMatrix<T> AeqTE;
Eigen::SparseMatrix<T> AeqTET;
// Debug
Eigen::SparseMatrix<T> NA;
Eigen::Matrix<T,Eigen::Dynamic,Eigen::Dynamic> NB;
};
#ifndef IGL_STATIC_LIBRARY
# include "min_quad_with_fixed.cpp"
#endif
#endif
only note this part:
// MIN_QUAD_WITH_FIXED Minimize quadratic energy
//
// 0.5*Z'*A*Z + Z'*B + C with
//
// constraints that Z(known) = Y, optionally also subject to the constraints
// Aeq*Z = BeqI would like to rewrite it in another form:

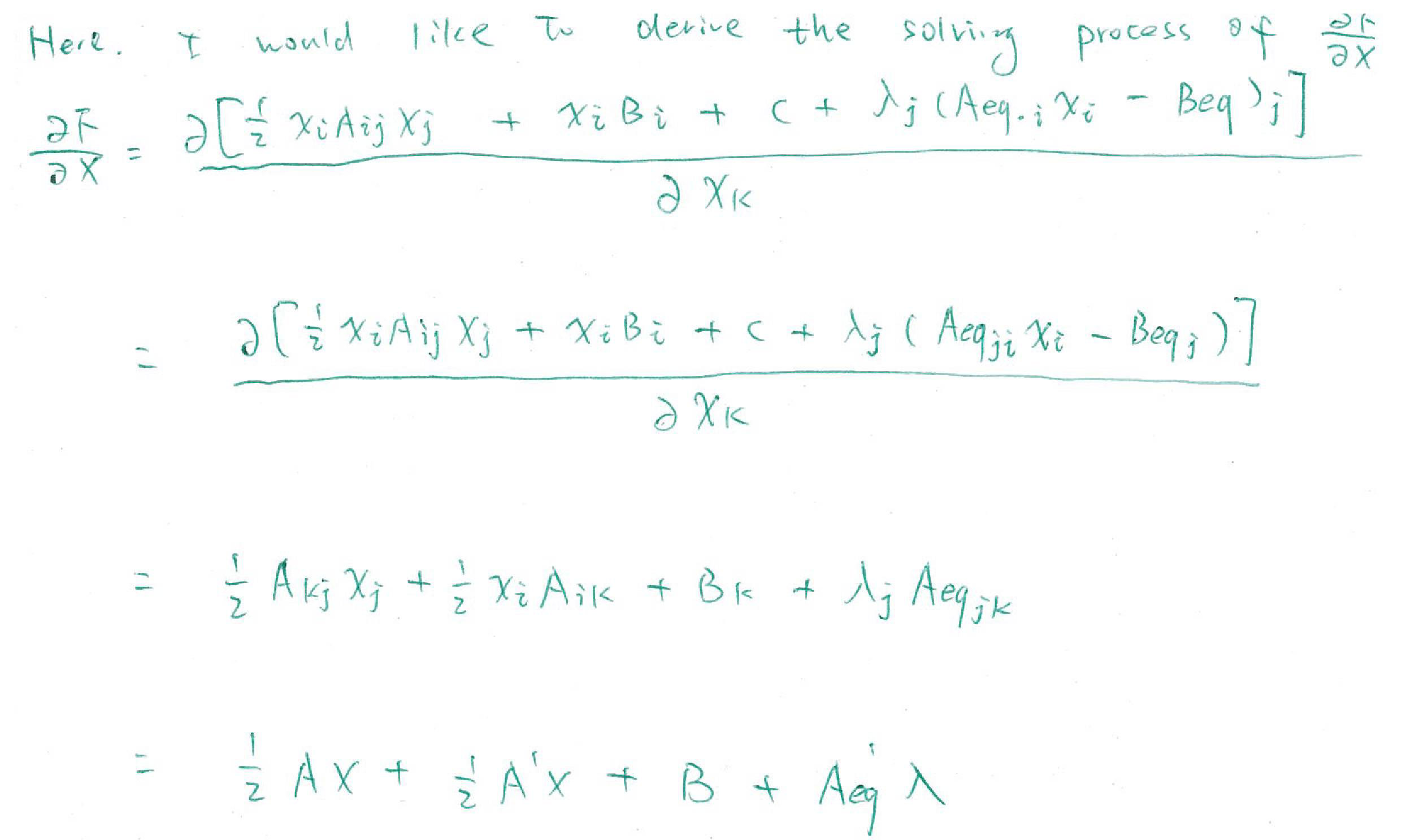
With this mathematical equation, it would be mush easier for us to read the source code.
we label the matrix equation as (*2).
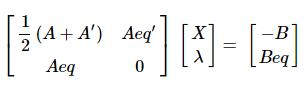 ................................................................................(*2)
................................................................................(*2)
Afterwards, we get into the harmonic.cpp
// This file is part of libigl, a simple c++ geometry processing library.
//
// Copyright (C) 2014 Alec Jacobson <alecjacobson@gmail.com>
//
// This Source Code Form is subject to the terms of the Mozilla Public License
// v. 2.0. If a copy of the MPL was not distributed with this file, You can
// obtain one at http://mozilla.org/MPL/2.0/.
#include "harmonic.h"
#include "cotmatrix.h"
#include "massmatrix.h"
#include "invert_diag.h"
#include "min_quad_with_fixed.h"
#include <Eigen/Sparse>
template <
typename DerivedV,
typename DerivedF,
typename Derivedb,
typename Derivedbc,
typename DerivedW>
IGL_INLINE bool igl::harmonic(
const Eigen::PlainObjectBase<DerivedV> & V,
const Eigen::PlainObjectBase<DerivedF> & F,
const Eigen::PlainObjectBase<Derivedb> & b,
const Eigen::PlainObjectBase<Derivedbc> & bc,
const int k,
Eigen::PlainObjectBase<DerivedW> & W)
{
using namespace Eigen;
typedef typename DerivedV::Scalar Scalar;
typedef Matrix<Scalar,Dynamic,1> VectorXS;
SparseMatrix<Scalar> L,M,Mi;
cotmatrix(V,F,L);
switch(F.cols())
{
case 3:
massmatrix(V,F,MASSMATRIX_TYPE_VORONOI,M);
break;
case 4:
default:
massmatrix(V,F,MASSMATRIX_TYPE_BARYCENTRIC,M);
break;
}
invert_diag(M,Mi);
SparseMatrix<Scalar> Q = -L;
for(int p = 1;p<k;p++)
{
Q = (Q*Mi*-L).eval();
}
const VectorXS B = VectorXS::Zero(V.rows(),1);
min_quad_with_fixed_data<Scalar> data;
min_quad_with_fixed_precompute(Q,b,SparseMatrix<Scalar>(),true,data);//Aeq传进去为0
W.resize(V.rows(),bc.cols());
for(int w = 0;w<bc.cols();w++)
{
const VectorXS bcw = bc.col(w);
VectorXS Ww;
if(!min_quad_with_fixed_solve(data,B,bcw,VectorXS(),Ww))//const VectorXS B = VectorXS::Zero(V.rows(),1);//这里Beq也为0
{
return false;
}
W.col(w) = Ww;
}
return true;
}
#ifdef IGL_STATIC_LIBRARY
// Explicit template specialization
template bool igl::harmonic<Eigen::Matrix<double, -1, -1, 0, -1, -1>, Eigen::Matrix<int, -1, -1, 0, -1, -1>, Eigen::Matrix<int, -1, 1, 0, -1, 1>, Eigen::Matrix<double, -1, 1, 0, -1, 1>, Eigen::Matrix<double, -1, 1, 0, -1, 1> >(Eigen::PlainObjectBase<Eigen::Matrix<double, -1, -1, 0, -1, -1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<int, -1, -1, 0, -1, -1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<int, -1, 1, 0, -1, 1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<double, -1, 1, 0, -1, 1> > const&, int, Eigen::PlainObjectBase<Eigen::Matrix<double, -1, 1, 0, -1, 1> >&);
template bool igl::harmonic<Eigen::Matrix<double, -1, -1, 0, -1, -1>, Eigen::Matrix<int, -1, -1, 0, -1, -1>, Eigen::Matrix<int, -1, 1, 0, -1, 1>, Eigen::Matrix<double, -1, -1, 0, -1, -1>, Eigen::Matrix<double, -1, -1, 0, -1, -1> >(Eigen::PlainObjectBase<Eigen::Matrix<double, -1, -1, 0, -1, -1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<int, -1, -1, 0, -1, -1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<int, -1, 1, 0, -1, 1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<double, -1, -1, 0, -1, -1> > const&, int, Eigen::PlainObjectBase<Eigen::Matrix<double, -1, -1, 0, -1, -1> >&);
template bool igl::harmonic<Eigen::Matrix<double, -1, -1, 0, -1, -1>, Eigen::Matrix<int, -1, -1, 0, -1, -1>, Eigen::Matrix<int, -1, -1, 0, -1, -1>, Eigen::Matrix<double, -1, -1, 0, -1, -1>, Eigen::Matrix<double, -1, -1, 0, -1, -1> >(Eigen::PlainObjectBase<Eigen::Matrix<double, -1, -1, 0, -1, -1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<int, -1, -1, 0, -1, -1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<int, -1, -1, 0, -1, -1> > const&, Eigen::PlainObjectBase<Eigen::Matrix<double, -1, -1, 0, -1, -1> > const&, int, Eigen::PlainObjectBase<Eigen::Matrix<double, -1, -1, 0, -1, -1> >&);
#endif
Here, matrix Q is like:
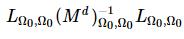
or, in the code expression way
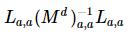
where subscript a stands for all vertices like k for known, u for unknown, l for lagrange (i.e. a = k + u)
function min_quad_with_fixed_precompute and min_quad_with_fixed_solve try to build the linear system and solve it.
Now, let's turn to min_quad_with_fixed.cpp to check those two functions. They are little bit complex, so here I just pick the important things to say:
In min_quad_with_fixed_precompute function,
const Eigen::SparseMatrix<T> A = 0.5*A2;// Due to the fact that the solution is doubled, they use half of A.where A2 is matrix Q above.
data.preY = Aulk + AkulT;in another form, it is like:
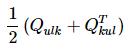
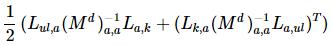
new_A = cat(1, cat(2, A, AeqT ),
cat(2, Aeq, Z ));Here A is assigned by Q above, which is:
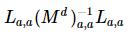
slice(new_A,data.unknown_lagrange,data.unknown_lagrange,NA);NA is like:
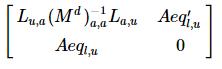 , whose size is
, whose size is 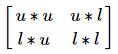
At this point, I've gotten the left side matrix of (*2), let's keep going upon the right side.
VectorXT BBeq(B.size() + Beq.size());
BBeq << B, (Beq*-2.0);
// Build right hand side
VectorXT BBequl;
igl::slice(BBeq,data.unknown_lagrange,BBequl);
MatrixXT BBequlcols;
igl::repmat(BBequl,1,cols,BBequlcols);//int cols = Y.cols(); here Y only has one column, if Y has multiple columns, so does the solution.
MatrixXT NB;
if(kr == 0)
{
NB = BBequlcols;
}else
{
NB = data.preY * Y + BBequlcols;// Y : const VectorXS bcw = bc.col(w); here Y only has one column, if Y has multiple columns, so does the solution.
}
data.preY * Y is like:
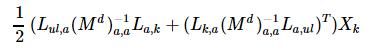
which is the matrix B on the right side of formula (*2)
BBeq << B, (Beq*-2.0);the whole linear system seems like :
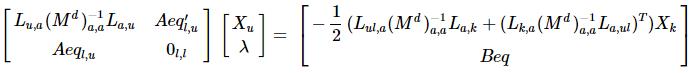
the one used in the code which yields the negative doubled X solution is like:
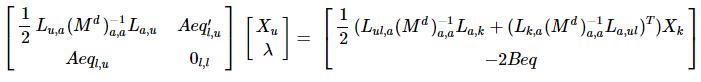
then using
sol *= -0.5;to get the real solution.
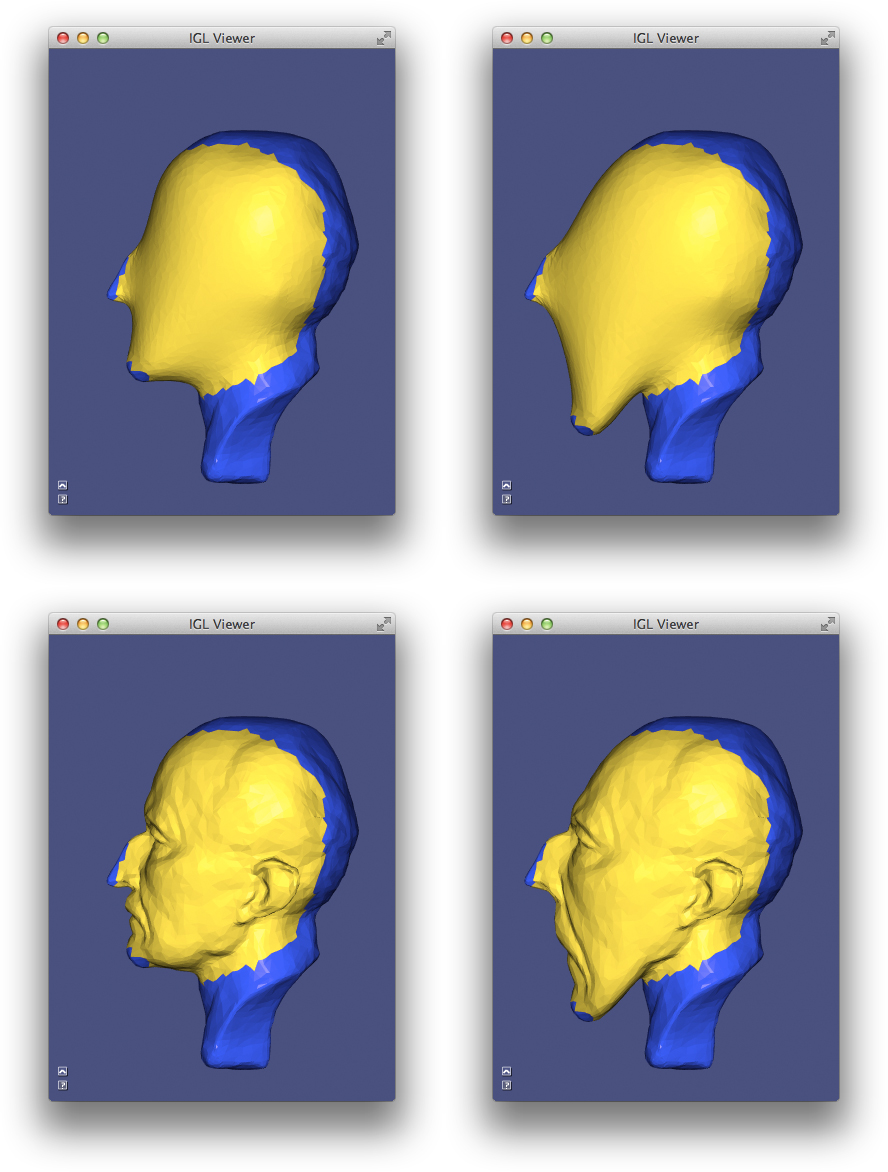
note: the yellow part in the mesh correspond to the -1 part in DMAT file which is calculated by this algorithm.
以上是关于401 biharmonic deformation的主要内容,如果未能解决你的问题,请参考以下文章