线性回归

Posted 2023-01-04 eastblue

1. 线性回归

核心公式：

 

 

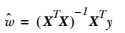
 w = (X^TX)^-1X^TY

 

流程伪代码：

读入数据，将数据特征x、特征标签y存储在矩阵x、y中
验证 x^Tx 矩阵是否可逆
使用最小二乘法求得 回归系数 w 的最佳估计

 

核心代码：

 1 def standRegres(xArr, yArr):
 2     xMat = mat(xArr)
 3     yMat = mat(yArr).T
 4     # 矩阵乘法的条件是左矩阵的列数等于右矩阵的行数
 5     xTx = xMat.T * xMat
 6     # 因为要用到xTx的逆矩阵，所以事先需要确定计算得到的xTx是否可逆，条件是矩阵的行列式不为0
 7     # linalg.det() 函数是用来求得矩阵的行列式的，如果矩阵的行列式为0，则这个矩阵是不可逆的，就无法进行接下来的运算
 8     if linalg.det(xTx) == 0.0:
 9         print("This matrix is singular, cannot do inverse")
10         return
11     # 最小二乘法
12     # 求得w的最优解
13     ws = xTx.I * (xMat.T * yMat)
14     return ws

 

 

2. 局部加权线性回归

（就是中间乘上权值W)

 

核心公式：

 参数w = (X^TWX)^-1X^TWY

权值Wi = exp( ||xi - x|| / ( -2*k²) )

 

流程伪代码：

读入数据，将数据特征x、特征标签y存储在矩阵x、y中
利用高斯核构造一个权重矩阵 W，对预测点附近的点施加权重
验证 X^TWX 矩阵是否可逆
使用最小二乘法求得 回归系数 w 的最佳估计

 

核心代码：

 1 def lwlr(testPoint, xArr, yArr, k=1.0):
 2     xMat = mat(xArr)
 3     yMat = mat(yArr).T
 4     # 获得xMat矩阵的行数
 5     m = shape(xMat)[0]
 6     # eye()返回一个对角线元素为1，其他元素为0的二维数组，创建权重矩阵weights，该矩阵为每个样本点初始化了一个权重
 7     weights = mat(eye((m)))
 8     for j in range(m):
 9         # testPoint 的形式是 一个行向量的形式
10         # 计算 testPoint 与输入样本点之间的距离，然后下面计算出每个样本贡献误差的权值
11         diffMat = testPoint - xMat[j, :]
12         # k控制衰减的速度
13         weights[j, j] = exp(diffMat * diffMat.T / (-2.0 * k ** 2))
14     # 根据矩阵乘法计算 xTx ，其中的 weights 矩阵是样本点对应的权重矩阵
15     xTx = xMat.T * (weights * xMat)
16     if linalg.det(xTx) == 0.0:
17         print("This matrix is singular, cannot do inverse")
18         return
19     # 计算出回归系数的一个估计
20     ws = xTx.I * (xMat.T * (weights * yMat))
21     return testPoint * ws