算法设计与分析——多边形游戏（动态规划）

Posted 2023-01-01 wkfvawl

一、问题描述

多边形游戏是一个单人玩的游戏，开始时有一个由n个顶点构成的多边形。每个顶点被赋予一个整数值，每条边被赋予一个运算符“+”或“*”。所有边依次用整数从1到n编号。

　　游戏第1步，将一条边删除。

　　随后n-1步按以下方式操作：

　　(1)选择一条边E以及由E连接着的2个顶点V1和V2；

　　(2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点。

　　最后，所有边都被删除，游戏结束。游戏的得分就是所剩顶点上的整数值。

　　问题:对于给定的多边形，计算最高得分。

如下图：

 

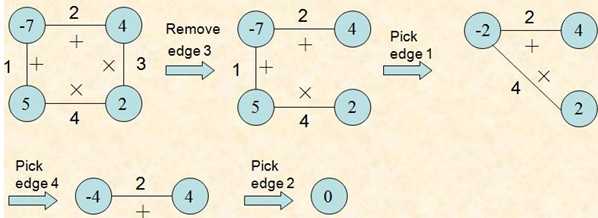
其实该问题与之前讨论过的凸多边形最优三角剖分问题是类似的，但二者的最优子结构性质却不同。多边形游戏问题的最优子结构性质更具有一般性。

二、算法思路

1、最优子结构性质

设所给的多边形的顶点和边的顺时针序列为op[1],v[1],op[2],v[2],op[3],…,op[n],v[n] 其中，op[i]表示第i条边所对应的运算符，v[i]表示第i个顶点上的数值，i=1~n。
       在所给的多边形中，从顶点i（1<=i<=n）开始，长度为j（链中有j个顶点）的顺时针链p(i,j）可表示为v[i],op[i+1],…,v[i+j-1]，如果这条链的最后一次合并运算在op[i+s]处发生（1<=s<=j-1），则可在op[i+s]处将链分割为两个子链p(i,s)和p(i+s,j-s)。
    设m[i,j,0]是链p(i,j)合并的最小值，而m[i,j,1]是最大值。若最优合并在op[i+s]处将p(i,j)分为两个长度小于j的子链的最大值和最小值均已计算出。即：
    a=m[i,s,0]  b=m[i,s,1]  c=m[i+s,j-s,0]  d=m[i+s,j-s,1]

   (1) 当op[i+s]=’+’时
    m[i,j,0]=a+c ；m[i,j,1]=b+d

   该链的最优性由子链的最优性决定，最大值对应于子链的最大值，最小值对应于子链的最小值。

   (2) 当op[i+s]=’*’时
    m[i,j,0]=minac,ad,bc,bd ； m[i,j,1]=maxac,ad,bc,bd
   由于v[i]可能取负数，子链的最大值相乘未必能得到主链的最大值，但是注意到，主链的最大值和最小值可以由子链的最大最小值得到。

    由于最优断开位置s有1<=s<=j-1的j-1中情况。 初始边界值为 m[i,1,0]=v[i]   1<=i<=n m[i,1,1]=v[i]   1<=i<=n

2、递归求解

可以得到递归表达式，将p(i,j)在op[i+s]处断开的最大值记为maxf(i,j,s)，最小值记为minf(i,j,s)则：

 

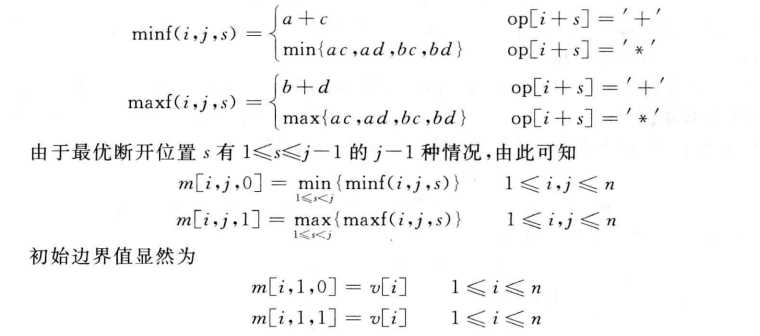
   因为多变形式封闭的，在上面的计算中，当i+s>n时，顶点i+s实际编号为(i+s)mod n。按上述递推式计算出的m[i,n,1]记为游戏首次删除第i条边后得到的最大得分。