机器学习：逻辑回归

Posted 2022-12-31 zhuchengchao

逻辑回归

理论分析

概述

? Logistic回归在本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数\\(g(z)\\)将上述结果映射到0-1上。

优点：计算代价不高，易于理解和实现

缺点：容易欠拟合，分类精度不高

适用数据：数值型和标称型

映射函数

sigmoid

• 函数表示

\\[ g(z)=\\frac11+e^-z \\]

\\[ z = \\theta_0+\\theta_1x_1+\\theta_2x_2+...+\\theta_nx_n \\]

• 导函数：

\\[ g^'(z)=g(z)(1-g(z)) \\]

• 函数图像

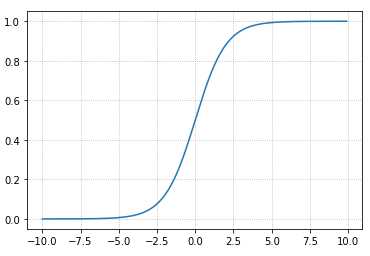
如下代码：

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10,10,0.1)
y = 1./(1.+np.exp(-x))
plt.grid(b=True, ls=':')
plt.plot(x, y)

逻辑回归及似然函数

首先假设：
\\[ P(y=1|x;θ)=h_θ(x) \\]

\\[ P(y=0|x;θ)=1-h_θ(x) \\]

\\[ P(y|x;θ)=(h_θ(x))^y(1-h_θ(x))^1-y \\]

根据似然函数如下：
\\[ L(θ)=P(Y|X;θ)=\\prod_i=1^mp(y^i|x^i;θ) \\]
取对数，为对数似然函数：
\\[ l(θ)=\\log L(θ)=\\sum_i=1^my^ilog(h_\\theta(x^i))+(1-y^i)log(1-h_\\theta(x^i)) \\]

注：\\(h_θ(x^i)=g(θ^Tx^i)\\)

损失函数

• 由上述的对数似然函数出以下结论：在取某θ时，数似然函数取最大值，表面此时的参数为最优；

• 由此将似然函数取反，定义完整的损失函数如下：

\\[ loss(h_\\theta(x),y)=-\\sum_i=1^my^ilog(h_\\theta(x^i))+(1-y^i)log(1-h_\\theta(x^i)) \\]

\\[ J(\\theta)=\\frac1m\\sum_i=1^mloss(h_\\theta(x^(i),y^(i))) \\]

\\[ minJ(\\theta) \\]

? 通过梯度下降对J(θ)进行求解，结果如下：
\\[ \\frac?J(\\theta)?\\theta_j=\\frac1m\\sum_i=1^m(g(θ^Tx^i)-y^i)x_j^i \\]
? 更新参数
\\[ \\theta_j=\\theta_j - \\alpha\\frac?J(\\theta)?\\theta_j \\]

正则化

同线性回归中梯度下降的正则化

实际应用

sklearn中API介绍

sklearn.linear_model.LogisticRegression(penalty=‘l2’, C = 1.0)

# Logistic回归分类器
# coef_：回归系数
# 注：默认使用了l2正则化

案例——肿瘤良性、恶性预测

# 导入必要的库
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler

# 读取数据
# 构造列标签名字
column = ['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']

# 读数据
data = pd.read_csv("./breast-cancer-wisconsin.data", names=column)
# print(data)

# 对缺失值进行处理
data = data.replace(to_replace="?", value=np.nan)

# 丢弃缺失值
data = data.dropna()

# 对数据进行分割
x_train, x_test, y_train, y_test = train_test_split(data[column[1:10]], data[column[10]], test_size=0.25)

# 进行标准化处理
std = StandardScaler()

x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)

# 逻辑回归预测
lg = LogisticRegression(C=1.0)

lg.fit(x_train, y_train)
print(lg.coef_)
# [[1.18661055 0.37775507 0.77048383 0.72337353 0.40801567 1.31255209  0.72011434 0.52286549 0.69823535]]

# 模型评估
y_predict = lg.predict(x_test)

# 准确率
print("准确率为：", lg.score(x_test, y_test))
# 准确率为： 0.9649122807017544

from sklearn.metrics import classification_report
# 召回率
print("召回率为：", classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"]))
# 召回率为：          precision  recall    f1-score    support
# 
#          良性       0.97      0.97      0.97       116
#          恶性       0.95      0.95      0.95        55
# 
# avg / total        0.96      0.96      0.96       171

• 其他参考代码，例如乳腺癌分类/鸢尾花数据分类，放置GitHub下：

https://github.com/zhuChengChao/ML-LogisticsRegression