Numpy基础：数组和矢量计算

Posted 2022-12-31 ymjun

《利用Python进行数据分析·第2版》第四章 Numpy基础：数组和矢量计算

numpy高效处理大数组的数据原因：

• numpy是在一个连续的内存块中存储数据，独立于其他python内置对象。其C语言编写的算法库可以操作内存而不必进行其他工作。比起内置序列，使用的内存更少（即时间更快，空间更少）

• numpy可以在整个数组上执行复杂的计算，而不需要借助python的for循环

4.0 前提知识

数据：结构化的数据代指所有的通用数据，如表格型，多维数组，关键列，时间序列等
相关包：numpy pandas matplotlib scipy scikit-learn statsmodels

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import statsmodels as sm

数据规整（Munge/Munging/Wrangling）：
指的是将非结构化和（或）散乱数据处理为结构化或整洁形式的整个过程。这几个词已经悄悄成为当今数据黑客们的行话了。Munge这个词跟Lunge押韵。

伪码（Pseudocode）：
算法或过程的“代码式”描述，而这些代码本身并不是实际有效的源代码。

语法糖（Syntactic sugar）:
这是一种编程语法，它并不会带来新的特性，但却能使代码更易读、更易写。

4.1 Numpy的ndarrray：一种多维数组对象

ndarray：N维数组对象，快速而灵活的大数据集容器

• 通用的同构数据多维容器(所有元素相同类型)
• 每个对象都有一个shape(表示各维度大小的元组)+dtype(表示数组数据类型的对象)+ ndim(维度)

对整块数据执行运算的语法=标量元素执行运算的语法

np.random.randn(n,m)：生成2行3列的正态分布随机数组

data = np.random.randn(2, 3)
array([[-0.2047, 0.4789, -0.5194],
[-0.5557, 1.9658, 1.3934]])

data * 10
array([[ -2.0471, 4.7894, -5.1944],
[ -5.5573, 19.6578, 13.9341]])

In [17]: data.shape
Out[17]: (2, 3)
In [18]: data.dtype
Out[18]: dtype('float64')

1）创建ndarray

np.array(一切对象)—>自动推断数据类型

np.zeros((n,m)) / np.ones((n,m)) / np.empty((n,m))：生成全0，全1，全未初始化垃圾值数组，传入元组/整数

np.arange()：range函数的numpy版本 如果没有特别指定，数据类型基本都是float64（浮点数）

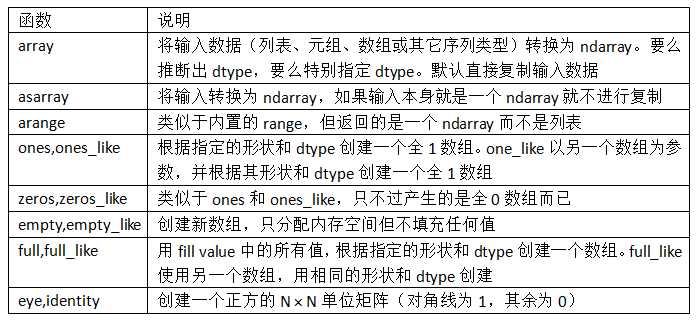
2）ndarray的数据类型

dtype是一个特殊的对象：含有ndarray将一块内存解释为特定数据类型所需的信息
—>命名方式：类型名+元素位长(float8字节64位长)

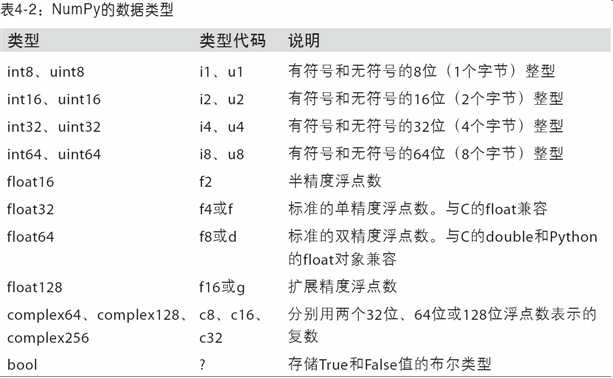
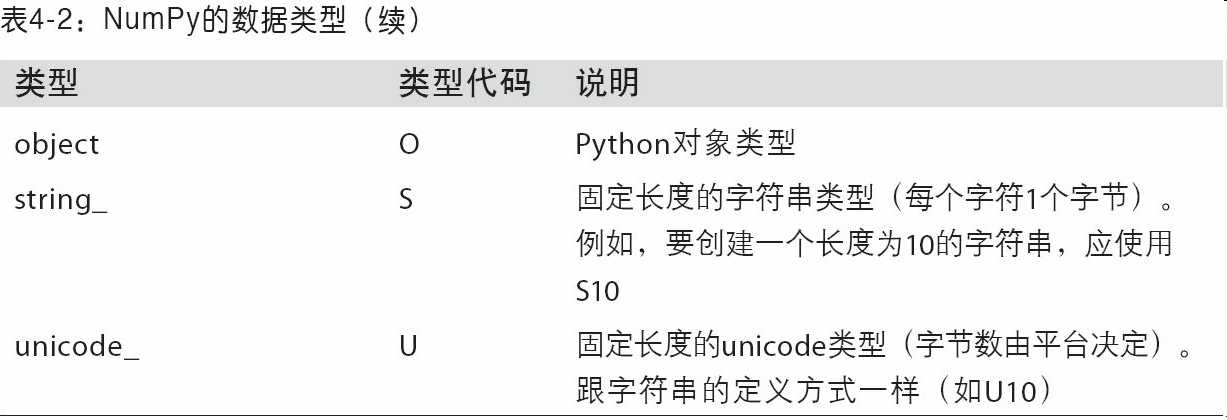
numpy会将 Python类型映射到等价的dtype上（如误写float映射为np.float64）
npo：在此简写为np类型的对象
npo.astype()：np强制类型转换

3）Numpy数组的运算

矢量化（vectorization）：大小相等的数组之间任何运算均应用到元素级

数组与标量的算术运算会将标量值广播到各个元素

大小相同的数组之间比较会生成布尔数组（逻辑运算）

4）基本的索引和切片

一维数组：
标量赋值切片时，标量值自动广播

数组切片是原始数组的视图，不同于python内置列表，切片上的修改会映射到源数组上
（内置列表的切片是新建一个列表不会改变源列表）——>一种是视图，另一种是副本：副本用npo.copy()

二维数组：
npo[0,2] —> 表示第一行第三列的数
npo[[0,1],2] —> 表示第一二行第三列的数

5）切片索引

一维数组同python列表
二维数组npo[n]，n表示行；npo[:n]，则表示取数组前n行；npo[:2,1:]，表示取前两行，除第一列外的元素数组

6）布尔型索引

一维布尔型数组可用于数组索引：一维布尔型数组长度==索引数组的行长度(轴长度) —>用于筛选
二维则需要大小相同才可做索引运算

比较运算(组合逻辑)得到布尔型索引—>比较运算可以用!= / 也可以用~()对条件进行否定
（用来反转条件好用）

布尔型数组中用 & 和 | ，而不用and or —>数据运算得到的布尔型索引数组是新数组

print(data)
print(data[names == 'tom',1:])  

[[ 0.16915065  0.15038684  0.34028728]  
[ 0.32732646  0.69241855  0.65203056]  
[ 0.84402175  0.77184234  0.48730057]  
[ 0.94376757  0.33876278  0.77287885]  
[ 0.58535219  0.50321862  0.28196336]]  

[[ 0.15038684  0.34028728]  
[ 0.50321862  0.28196336]]

（注意： 原书中翻译“通过布尔型索引选取数组中的数据，将总是创建数据的副本，即使返回一模一样的数组也是如此。”<该处翻译可能有误>，因为如下）

In [113]: data[data < 0] = 0
In [114]: data
Out[114]:
array([[ 0.0929, 0.2817, 0.769 , 1.2464],
[ 1.0072, 0. , 0.275 , 0.2289],
[ 1.3529, 0.8864, 0. , 0. ],
[ 1.669 , 0. , 0. , 0.477 ],
[ 3.2489, 0. , 0. , 0.1241],
[ 0.3026, 0.5238, 0.0009, 1.3438],
[ 0. , 0. , 0. , 0. ]])

可以通过布尔索引对数组进行赋值，证明布尔索引得到的数据是视图而非副本

7）花式索引

numpy术语，利用整数数组进行索引

In [119]: arr
Out[119]:
array([[ 0., 0., 0., 0.],
[ 1., 1., 1., 1.],
[ 2., 2., 2., 2.],
[ 3., 3., 3., 3.],
[ 4., 4., 4., 4.],
[ 5., 5., 5., 5.],
[ 6., 6., 6., 6.],
[ 7., 7., 7., 7.]])
In [120]: arr[[4, 3, 0, 6]]
Out[120]:
array([[ 4., 4., 4., 4.],
[ 3., 3., 3., 3.],
[ 0., 0., 0., 0.],
[ 6., 6., 6., 6.]])

花式索引在选择索引行、列上使用频繁（1.一个[]就是一个维度，逗号分割维度 2.按照[]内顺序进行筛选
负数索引从末尾开始选取行

npo[[行],[:，列]]，扩展同理（后面格式必须得这样，否则会出现预期不一样的结果

array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23],
[24, 25, 26, 27],
[28, 29, 30, 31]])
In [124]: arr[[1, 5, 7, 2], [0, 3, 1, 2]]        #这种格式相当于是[1,0],[5,3]....
Out[124]: array([ 4, 23, 29, 10])
In [125]: arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]]        #这种格式才是预期的结果，把第一行的第0,3,1,2列都拿出来,再是第五行的....
Out[125]:
array([[ 4, 7, 5, 6],
[20, 23, 21, 22],
[28, 31, 29, 30],
[ 8, 11, 9, 10]])

花式索引！=切片，花式索引是副本而非视图

8）数组转置和轴对换

npo.T属性：数组的转置数组（方法一：针对一二维数组：返回视图非副本
npo.transpose(arry_method)（方法二：针对高维数组：返回视图非副本 arry_method：由轴编号组成的元组 / 轴就是维度
transpose方法结合npo.shape进行 —>

In [60]: arr1 
Out[60]: array([[[ 0, 1, 2], [ 3, 4, 5]], [[ 6, 7, 8], [ 9, 10, 11]]]) 
In [61]: arr1.shape #看形状 
Out[61]: (2, 2, 3) #说明这是一个2*2*3的数组（矩阵），返回的是一个元组，可以对元组进行索引，也就是0,1,2，维度进行编号

In [134]: arr.transpose((1, 0, 2))    #这里的(1,0,2)元组就相当是维度元组(0,1,2) 说明把第三维和第二维进行了交换（一般而言保持第一维度不会变化
Out[134]:
array([[[ 0, 1, 2, 3],            #比如数值6，原本是(1,0,0)的位置，变换后是(0,1,0)
[ 8, 9, 10, 11]],
[[ 4, 5, 6, 7],
[12, 13, 14, 15]]])

np.dot()：计算矩阵内积 —>np.dot(npo.T,npo)
npo.swapaxes(arry_method)（方法三：实现两个维度的交换：返回视图非副本 arry_method：接受一对轴编号 / 就是两个维度

转置和轴对换

4.2 通用函数：快速的元素级数组函数 ufunc

简单函数（接受一个或多个标量值，并产生一个或多个标量值）的矢量化包装器。

一元ufunc（接受一个矢量）：np.sqrt np.exp... 一元：unary
二元ufunc： np.add() np.maximum... 二元：binary
返回多个数组：np.modf（内置函数divmod的矢量化版本：divmod(a,b) / 返回一个包含shan商和余数的元组(a//b，a%b)
//更确切说是math库中modf的矢量化版本：将数组各元素的小数部分和整数部分以两个独立数组形式返回

ufunc可接受一个out可选参数：表示在传入数组上原地进行操作（即结果值返回至数组中
部分一元、二元ufunc

4.3利用数组进行数据处理

np.meshgrid()：生成网格点坐标矩阵 //强烈的规律性快速生成矩阵

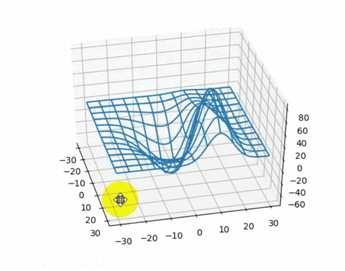
图中每个交叉点都是网格点；网格点的坐标的矩阵就是坐标矩阵

xs, ys = np.meshgrid(points, points)

传入参数为两个一维数组，分别是所有的x、y值
返回产生的两个二维数组，分别是按网格状化后排列的x、y值

numpy.meshgrid()理解

1）将条件逻辑表述为数组运算

np.where()：三元表达式 x if condition else y 的矢量化版本
条件：布尔矩阵 if：第二个参数 else：第三个参数 返回：产生的新数组

In [165]: xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
In [166]: yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
In [167]: cond = np.array([True, False, True, True, False])    #cond为True时，选取xarr的值，否则从yarr中选取。
In [168]: result = [(x if c else y)                #列表生成式写法
.....: for x, y, c in zip(xarr, yarr, cond)]
In [169]: result
Out[169]: [1.1000000000000001, 2.2000000000000002, 1.3, 1.3999999999999999, 2.5]    #1.大数据处理慢  2.无法用于多维数组(多个for时间度问题

In [170]: result = np.where(cond, xarr, yarr)        #np.where解决
In [171]: result
Out[171]: array([ 1.1, 2.2, 1.3, 1.4, 2.5])

np.where作用：根据另一个数组而产生一个新数组；
第二三个参数不一定是矢量，也可以是标量

In [173]: arr
Out[173]:
array([[-0.5031, -0.6223, -0.9212, -0.7262],
[ 0.2229, 0.0513, -1.1577, 0.8167],
[ 0.4336, 1.0107, 1.8249, -0.9975],
[ 0.8506, -0.1316, 0.9124, 0.1882]])
In [174]: arr > 0
Out[174]:
array([[False, False, False, False],
[ True, True, False, True],
[ True, True, True, False],
[ True, False, True, True]], dtype=bool)
In [175]: np.where(arr > 0, 2, -2)
Out[175]:
array([[-2, -2, -2, -2],
[ 2, 2, -2, 2],
[ 2, 2, 2, -2],
[ 2, -2, 2, 2]])

2）数学和统计方法

聚合计算：(aggregation，通常叫约简(reduction)) 聚类统计

np.sum np.mean np.std... 求和平均标准差 可以对整个数组 / 也可以接受一个axis计算对某轴的统计值
axis=1(行) axis=0(列)

非聚合计算：np.cumsum np.cumprod... 累加累乘 产生一个结果数组（多维数组中一样，可以指定轴)

3）用于布尔型数组的方法

布尔型数组也可用于统计方法—>转为1 / 0

（sum求True个数
（any是否存在True （all是否都是True 同样适用于数值数组

4）排序

npo.sort()：原地排序 （多维数组加axis

np.sort返回副本，npo.sort原地修改本身

计算数组分位数：1.排序 2.选取特定位置值

In [203]: large_arr = np.random.randn(1000)
In [204]: large_arr.sort()
In [205]: large_arr[int(0.05 * len(large_arr))] # 5% quantile
Out[205]: -1.5311513550102103

其他排序：附录+pandas

5）唯一化以及其他的集合逻辑

集合函数

np.unique()：找出数组中唯一值并返回排序结果 = set+sorted
np.in1d()：试探一个数组的值在另一个数组中的成员是否包含，返回布尔型数组

4.4 用于数组的文件输入输出（较为简单的fIO)

np.save：数组以未压缩的原始二进制格式 扩展名：.npy
np.savez：多个数组保存到一个未压缩文件中，数组以关键字参数形式传入 扩展名：.npz
np.load：加载.npy正常 加载.npz时得到类似字典的对象：对各个数组进行延迟加载(类似迭代器，惰性计算
np.savez_compressed：数据压缩

4.5线性代数

x.dot(y) = np.dot(x,y) ：矩阵乘法 所有数组dot方法和np命名空间函数的区别是：dot方法是视图，函数是副本

@符(类似python3.5)也可以作为中缀运算符进行矩阵乘法：

In [230]: x @ np.ones(3)
Out[230]: array([ 6., 15.])

numpy.linalg中有一组标准的矩阵分解运算以及如求逆和行列式等：
In [231]: from numpy.linalg import inv, qr In [232]: X = np.random.randn(5, 5) In [233]: mat = X.T.dot(X) In [234]: inv(mat) Out[234]: array([[ 933.1189, 871.8258, -1417.6902, -1460.4005, 1782.1391], [ 871.8258, 815.3929, -1325.9965, -1365.9242, 1666.9347], [-1417.6902, -1325.9965, 2158.4424, 2222.0191, -2711.6822], [-1460.4005, -1365.9242, 2222.0191, 2289.0575, -2793.422 ], [ 1782.1391, 1666.9347, -2711.6822, -2793.422 , 3409.5128]]) In [235]: mat.dot(inv(mat)) #求逆 Out[235]: array([[ 1., 0., -0., -0., -0.], [-0., 1., 0., 0., 0.], [ 0., 0., 1., 0., 0.], [-0., 0., 0., 1., -0.], [-0., 0., 0., 0., 1.]]) In [236]: q, r = qr(mat) #qr矩阵分解 In [237]: r Out[237]: array([[-1.6914, 4.38 , 0.1757, 0.4075, -0.7838], [ 0. , -2.6436, 0.1939, -3.072 , -1.0702], [ 0. , 0. , -0.8138, 1.5414, 0.6155], [ 0. , 0. , 0. , -2.6445, -2.1669], [ 0. , 0. , 0. , 0. , 0.0002]])

4.6 伪随机数生成

np.random.normal：标准正态分布
np.random.seed：设置随机数生成种子（全局状态种子
np.random.RandomState：创建一个与其他隔离的随机数生成器（局部状态种子）

4.7 示例：随机漫步

纯python：

In [247]: import random
.....: position = 0
.....: walk = [position]
.....: steps = 1000
.....: for i in range(steps):
.....: step = 1 if random.randint(0, 1) else -1
.....: position += step
.....: walk.append(position)
.....:

转为numpy：

In [251]: nsteps = 1000
In [252]: draws = np.random.randint(0, 2, size=nsteps)    #size决定是一维的
In [253]: steps = np.where(draws > 0, 1, -1)
In [254]: walk = steps.cumsum()

In [249]: plt.plot(walk[:100])        #x步数也就是时间，y是离初始点的距离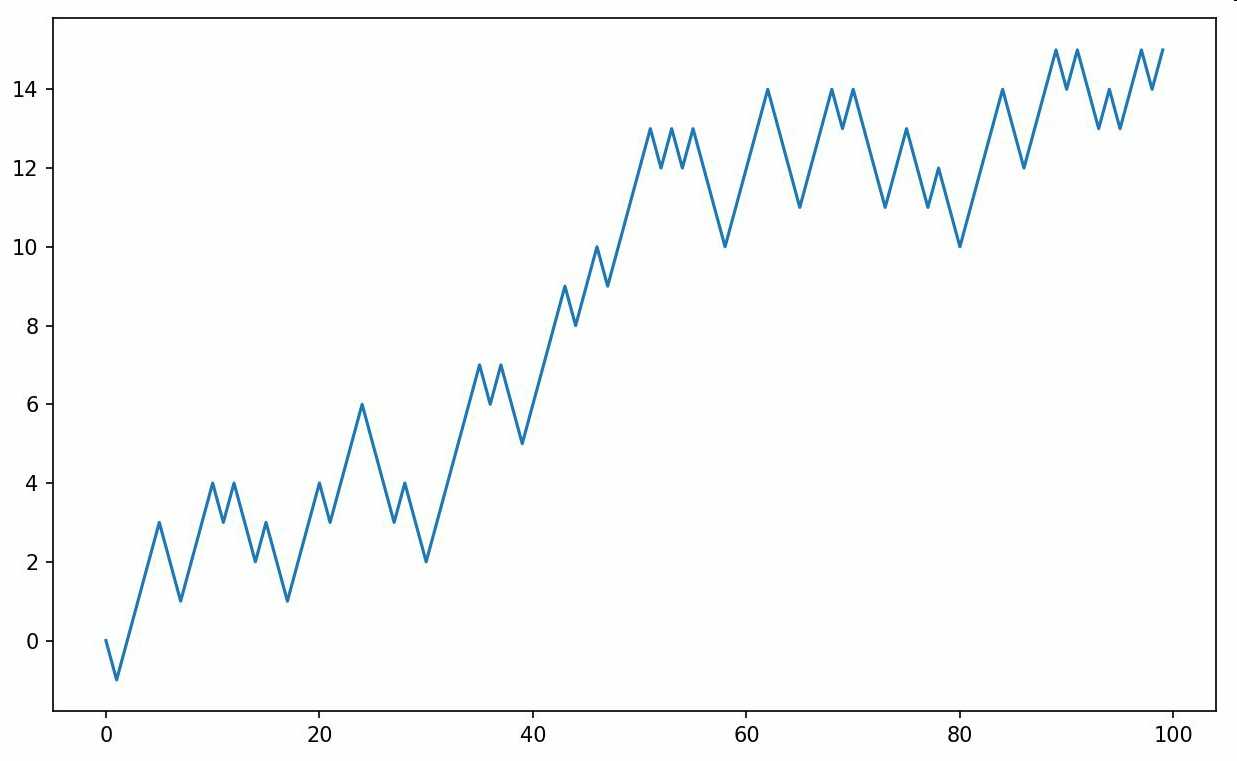

对l累加后的漫步数据一些统计计算处理：

In [255]: walk.min()
Out[255]: -3
In [256]: walk.max()
Out[256]: 31

假设离初始点距离10步外就是穿越过了漫步地点，想要知道首次穿越时间：

In [257]: (np.abs(walk) >= 10).argmax()    #argmax返回数组最大值的第一个索引位置
Out[257]: 37                    #所以第37步时第一次走出漫步地点

一次性模拟多个随机漫步：

In [258]: nwalks = 5000
In [259]: nsteps = 1000
In [260]: draws = np.random.randint(0, 2, size=(nwalks, nsteps)) # 0 or 1    #size决定是二维的 行：第几次walk 列：nwalk的第几步
In [261]: steps = np.where(draws > 0, 1, -1)
In [262]: walks = steps.cumsum(1)        #按行作累加 / 非聚合
In [263]: walks
Out[263]:
array([[ 1, 0, 1, ..., 8, 7, 8],
[ 1, 0, -1, ..., 34, 33, 32],
[ 1, 0, -1, ..., 4, 5, 4],
...,
[ 1, 2, 1, ..., 24, 25, 26],
[ 1, 2, 3, ..., 14, 13, 14],
[ -1, -2, -3, ..., -24, -23, -22]])

计算所有随机漫步的统计数据：

In [264]: walks.max()        
Out[264]: 138
In [265]: walks.min()
Out[265]: -133

之后计算每个随机漫步的首次穿越时间：阈值=30（注：不是每次漫步都能够穿越，所以需要清理检查

In [266]: hits30 = (np.abs(walks) >= 30).any(1)        #按行筛选每行是不是有abs>30的值
In [267]: hits30
Out[267]: array([False, True, False, ..., False, True, False], dtype=bool)
In [268]: hits30.sum() # Number that hit 30 or -30        #为True的就是满足要求的，一共有3410个
Out[268]: 3410

获取穿越时间：

In [269]: crossing_times = (np.abs(walks[hits30]) >= 30).argmax(1)    #花式索引筛选满足要求行+argmax找到首次穿越的时间
In [270]: crossing_times.mean()
Out[270]: 498.88973607038122