1006

Posted 2022-12-29 oieredsion

hh A题算了下空间感觉没问题 没想到开了4个数组 成功bao 0
期望290 实际 175
naiive

A.劳伦斯数
数学家劳伦斯定义： 对于任意整数 x， 如果 x 是素数， 或者 x 可以表示成两个素数的乘积， 那
么 x 就称为劳伦斯数。
现在给出 Q 个询问， 每个询问形如“L R” ， 需要你快速统计出区间[L,R]中有多少个劳伦斯
数。
解：
这题肯定和线性筛有关系
然后打了一波板子后 发现 对于x 表示成两个素数的乘积的形式 我们可以这样想想
当i是一个质数 那么i*pri[j] 就会满足条件 并且由于线性筛的特性 pri[j] 一定是一个最小的质因数

就像这样

    if(phi[le]==i)
            
                p[i*phi[j]]=1;
            

或者定义pr[x] 表示x 的最小质因数
那么充要条件为 pr[i/pr[i]]=i/pr[i]; 即最小的质因数是自己就满足素数的条件

考完后我发现自己还是太naiive
看到可能int 溢出不知道强制类型转换 省掉空间
看到标记的数组还开long long
1e9+1 搞定的事情 自己非要数着写

B.逃离迷宫
文件名： escape.cpp
输入输出名： escape.in/escape.out
时空限制 1s， 256m
题目描述
队员们在玩一款迷宫游戏。 在一个山体迷宫中， 共有 N 个山洞， 编号 1 到 N。
游戏开始时， 队员们位于 1 号山洞， 出口在 N 号山洞。 每个山洞里面可能有一些通行卡， 进入
一个山洞， 队员们就能获得该山洞的通行卡。 通行卡有 K 种， 编号 1 到 K。 山洞之间存在单向道路,
每条道路都需要拥有指定编号的通行卡才能通过。
通过一条道路的时间是 1 分钟， 队员们想知道， 最少多少分钟， 就能走到出口。
输入格式：
第一行， 三个整数 N,M,K， 表示山洞数、 道路数和通行卡种数
接下来 K 行， 其中第 i 行描述 i 号山洞存在的通行卡的情况， 用 N 个空格间隔的 0 或 1 来表
示。 若其中第 j 个数为 1， 表示该山洞存在 j 号通行卡， 为 0 则表示不存在第 j 号通行卡。
接下来 M 行， 每行描述一条道路的情况。 首先是两个数 X 和 Y， 表示有一条从 X 出发到达 Y
的通道。 接下来 K 空格间隔的个 0 或 1， 表示通过该通道需要拥有的通行卡的情况， 若其中第 j 个
数为 1， 表示需要 j 号通行卡， 为 0 则表示不需要。
输出格式：
一个整数， 表示最少所需时间。 若无法到达出口， 输出“No Solution” 。
样例输入：
3 3 2
1 0
0 1
0 0
1 3 1 1
1 2 1 0
2 3 1 1
样例输出：
2

解：
多维最短路+状压DP
定义f[i][j] 表示 在i 号点 集合为j 所需要的最小时间
满足条件： $ ((r.s$ & $ le[i])==le[i])$
转移为: $
if(dis[r.f][r.s]+1<dis[u][(r.s)|w[u]])

dis[u][(r.s)|w[u]]=dis[r.f][r.s]+1,
if(!mark[u][(r.s)|w[u]])

mark[u][(r.s)|w[u]]=1;


$

代码:

//
#include<bits/stdc++.h>
using namespace std;
#define maxnn 6010
int mark[maxnn][1<<11];
int n,m,k;
int all=0;
int las[maxnn],en[maxnn],le[maxnn],tot,nex[maxnn];
int dis[maxnn][1<<11];
int w[maxnn];
typedef pair<int ,int > P;
#define f first 
#define s second
#define inf 100000000
void add(int a ,int b,int c)

    en[++tot]=b;
    nex[tot]=las[a];
    las[a]=tot;
    le[tot]=c;

void spfa()

    queue<P> Q;
    for(int i=1;i<=n;i++)
    
        for(int j=0;j<=all;j++)
            dis[i][j]=inf;
            mark[i][j]=0;
        
    
    dis[1][w[1]]=0;
    mark[1][w[1]]=1;
    Q.push(make_pair(1,w[1]));
    while(Q.size())
    
        P r=Q.front();
        Q.pop();
        mark[r.f][r.s]=0;
        for(int i=las[r.f];i;i=nex[i])
        
            int u=en[i];
            if(!((r.s&le[i])==le[i]))continue;
            if(dis[r.f][r.s]+1<dis[u][(r.s)|w[u]])
            
                dis[u][(r.s)|w[u]]=dis[r.f][r.s]+1;
                if(!mark[u][(r.s)|w[u]])
                
                    mark[u][(r.s)|w[u]]=1;
                    Q.push(make_pair(u,(r.s)|w[u]));
                
            
        
    


void FIE()

    freopen("escape.in","r" ,stdin);
    freopen("escape.out","w",stdout);

int main()

    //FIE();
    int x,y,z;
    scanf("%d%d%d",&n,&m,&k);
    all=(1<<k)-1;
    for(int i=1;i<=n;i++)
    
        for(int j=1;j<=k;j++)
            scanf("%d",&z);
            if(z==1)
            w[i]=w[i]|((1<<j-1));
        
    
    for(int i=1;i<=m;i++)
    
        scanf("%d%d",&x,&y);
        int tmp=0;
        for(int j=1;j<=k;j++)
            cin>>z;
            if(z==1)
            tmp=tmp|((1<<j-1));
        
        add(x,y,tmp);
    
    spfa();
    int ans=100000000;
    for(int i=0;i<=all;i++)
        ans=min(ans,dis[n][i]);
    
    if(ans==100000000)
    
        puts("No Solution");
    
    else
    printf("%d",ans);

C 线路重叠
某城市有非常发达的公共交通系统。 有 N 个公交站， 通过 N-1 条双向道路连接起来。 公交站编
号 1 到 N， 任意两个公交站都可以相互到达。
队员们提出 Q 个询问， 每个询问形如“X Z Y” ， 表示问从 X 到 Z 的公交线路， 与从 Y 到 Z 的
公线路， 存在多少个重叠的车站。 重叠指车站既在 X 到 Z 路线中， 也在 Y 到 Z 路线中。
输入格式：
第一行， 两个整数 N 和 Q， 表示询问数
接下来 N-1 行， 每行两个整数 X 和 Y， 表示编号 X 和 Y 的公交站存在道路相连。
接下来 Q 行， 每行三个整数 X,Z,Y， 表示一次询问
输出格式：
Q 行， 每行一个整数， 对应一次询问的答案
样例输入：
3 3
1 2
2 3
1 2 3
1 1 3
3 1 3
样例输出：
1 1 3

解：
考场上没有注意到这是一个固定终点的问题 敲了一发树剖 T 75 旁边的某位ruan姓jul 打的比我复杂T90 我... 充分证明了fread 的重要性 时间复杂度\\(O(Q \\times （log2(n)）^2)\\)
考试后 利用树状数组优化 还是T90...
树剖的想法很好想
对于一段距离 在这条路径上+1 对于另一段距离 在他的路径上查询区间和 然后删去
发一波我写的树状数组的树剖

\\((k+1) \\sum c[i] - \\sum x*c[i]\\)
x 与 k 均为 add和get 函数里面 i的初始值

inline void add(int a ,int b) 
    en[++tot]=b;
    nex[tot]=las[a];
    las[a]=tot;

inline void ad1(int x,int d)

    for(int i=x;i<=n+100;i+=lowbit(i))
    
        c1[i]+=d;
    

inline void ad2(int x,int d)

    for(int i=x;i<=n+100;i+=lowbit(i))
    
        c2[i]=c2[i]+x*d;
    

inline int get1(int x)

    int ans=0;
    for(int i=x;i;i-=lowbit(i))
    
        ans=ans+(x+1)*c1[i];
    
    return ans;

inline int get2(int x)

    int ans=0;
    for(int i=x;i;i-=lowbit(i))
    
        ans+=c2[i];
    
    return ans;

//

#include<bits/stdc++.h>
using namespace std;
#define maxnn 1000000
#define maxn 500100
#define ll long long
#define lowbit(i) i&(-i) 
char pbuf[1<<20],*pf=pbuf;
inline void push(char c)

    if(pf-pbuf==(1<<20))fwrite(pbuf,1,1<<20,stdout),pf=pbuf;
    *pf++=c;

template<typename T>
inline void print(T x)

    static short sta[35];
    if(x<0)push('-'),x=-x;
    int TOP=0;
    dosta[TOP++]=x%10;x/=10;while(x);
    while(TOP)push('0'+sta[--TOP]);
    push('\\n');

char buf[1<<20],*p1,*p2;
#define GC (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?0:*p1++)
inline int R()

    char t=GC;
    int x=0;
    while(!isdigit(t)) t=GC;
    while(isdigit(t)) x=x*10+t-48,t=GC;
    return x;

int c1[maxnn],c2[maxnn];
int las[maxn],en[maxn],tot,nex[maxn];
int n,Q;
inline void add(int a ,int b) 
    en[++tot]=b;
    nex[tot]=las[a];
    las[a]=tot;

inline void ad1(int x,int d)

    for(int i=x;i<=n+100;i+=lowbit(i))
    
        c1[i]+=d;
    

inline void ad2(int x,int d)

    for(int i=x;i<=n+100;i+=lowbit(i))
    
        c2[i]=c2[i]+x*d;
    

inline int get1(int x)

    int ans=0;
    for(int i=x;i;i-=lowbit(i))
    
        ans=ans+(x+1)*c1[i];
    
    return ans;

inline int get2(int x)

    int ans=0;
    for(int i=x;i;i-=lowbit(i))
    
        ans+=c2[i];
    
    return ans;

int f[maxn][20];
int dfn[maxnn],cnt;
inline int go_up(int s,ll k) 
    int d=log2(n);
    for(int i=d; i>=0; i--) 
        if(k&(1<<i)) 
            s=f[s][i];
        
    
    return s;

ll dep[maxnn];
int topp[maxnn];
int son[maxn];
inline int lca(int x,int y) 
    if(dep[x]<dep[y])
        swap(x,y);
    int s=dep[x]-dep[y];
    x=go_up(x,s);
    if(x==y) return y;
    s=log2(n);
    for(int i=s; i>=0; i--) 
        if(f[x][i]!=f[y][i]) 
            x=f[x][i];
            y=f[y][i];
        
    
    return f[y][0];

ll size[maxn];
inline void dfs1(int v,int fa) 
    int maxson=-1;
    f[v][0]=fa;
    dep[v]=dep[fa]+1;
    int s=log2(n);
    for(int i=1; i<=s; i++) 
        f[v][i]=f[f[v][i-1]][i-1];
    
    size[v]=1;
    for(int i=las[v]; i; i=nex[i]) 
        int u=en[i];
        if(u!=fa) 
            dfs1(u,v);
            size[v]+=size[u];
            if(size[u]>maxson)
            
                maxson=size[u];
                son[v]=u;
            
        
    

inline void dfs2(int v,int fa,int t) 
    topp[v]=t;
    dfn[v]=++cnt;
    if(son[v]) dfs2(son[v],v,t);
    for(int i=las[v]; i; i=nex[i]) 
        int u=en[i];
        if(u!=fa&&u!=son[v]) 
            dfs2(u,v,u);
        
    

inline void add1(int x,int y,int d)

    while(topp[x]!=topp[y])
        if(dep[topp[x]]<dep[topp[y]])
        
            swap(x,y);
        
        ad1(dfn[topp[x]],d);
        ad1(dfn[x]+1,-d);
        ad2(dfn[topp[x]],d);
        ad2(dfn[x]+1,-d);
        x=f[topp[x]][0];
    
    if(dep[x]<dep[y])
        
            swap(x,y);
        
    ad1(dfn[y],d);
    ad1(dfn[x]+1,-d);
    ad2(dfn[y],d);
    ad2(dfn[x]+1,-d);

inline int get(int x,int y)

    int ans=0;
    while(topp[x]!=topp[y])
        if(dep[topp[x]]<dep[topp[y]])
        
            swap(x,y);
        
        int tmp1=dfn[topp[x]];
        int tmp2=dfn[x];
        ans=ans+(get1(tmp2)-get2(tmp2)-(get1(tmp1-1)-get2(tmp1-1)));
        x=f[topp[x]][0];
    
        if(dep[x]<dep[y])
        
            swap(x,y);
        
        int tmp1=dfn[y];
        int tmp2=dfn[x];
        ans=ans+(get1(tmp2)-get2(tmp2)-(get1(tmp1-1)-get2(tmp1-1)));
        return ans;

inline void ch1(int x,int y) 
    if(dep[x]<dep[y]) swap(x,y);
    int now=lca(x,y);
    if(now!=y) 
        add1(now,now,1);
        int tmp1=dep[x]-dep[now];
        int id1=go_up(x,tmp1-1);
        add1(id1,x,1);
        tmp1=dep[y]-dep[now];
        int id2=go_up(y,tmp1-1);
        add1(id2,y,1);
     else 
        add1(y,x,1);
    

inline ll ch2(int x,int y) 
    ll ans=0;
    if(dep[x]<dep[y]) swap(x,y);
    int now=lca(x,y);
    if(now!=y) 
        ans+=get(now,now);
        int tmp1=dep[x]-dep[now];
        int id1=go_up(x,tmp1-1);
        ans+=get(id1,x);
        tmp1=dep[y]-dep[now];
        int id2=go_up(y,tmp1-1);
        ans+=get(id2,y);
     else 
        ans+=get(y,x);
    
    return ans;

inline void era(int x,int y) 
    if(dep[x]<dep[y]) swap(x,y);
    int now=lca(x,y);
    if(now!=y) 
        add1(now,now,-1);
        int tmp1=dep[x]-dep[now];
        int id1=go_up(x,tmp1-1);
        add1(id1,x,-1);
        tmp1=dep[y]-dep[now];
        int id2=go_up(y,tmp1-1);
        add1(id2,y,-1);
     else 
        add1(y,x,-1);
    

int u;
void FIE()

    freopen("overlap1.in","r" ,stdin);
    freopen("op.out","w",stdout);

int main() 
    //FIE();
    n=R();
    Q=R();
    u=R();
    int x,y,z;
    for(int i=1; i<n; i++) 
        x=R();
        y=R();
        add(x,y);
        add(y,x);
    
    dfs1(1,0);
    dfs2(1,0,1);
    while(Q--) 
        x=R();
        z=R();
        y=R();
        ch1(x,z);
        int ans=ch2(y,z);
        print(ans);
        era(x,z);
       
 fwrite(pbuf,1,pf-pbuf,stdout);

下面是倍增的想法：
注意到终点是固定的
那么也就是说x或者y或者z 应该是与另一个点 到一个汇点 然后再一起到终点的

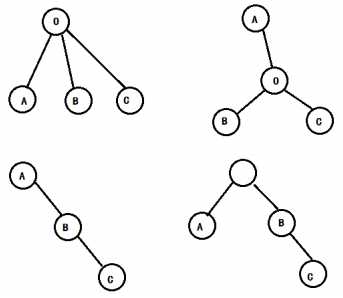
官方题解:
问题实际上是问树上一个点到另外两点路径的重合长度
树上三点，或是呈一条链的形式，或是存在一个中心，使得中心到三点之间的路径不相交。如下图，上方的两种情况是A、B、C点存在中心O，下方两种情况是A、B、C点在一条链上。对于呈一条链的形式，我们不妨将三个点中，位于中间的那个点称为三个点的中心，如此一来，我们要求的答案实际上是中心到B点的距离。那么，如何求中心呢？通过观察上图，我们发现，中心一定是A、B、C点中两点的LCA。并且，通过进一步观察，我们可以发现，中心是A、B、C点两两的LCA中，深度最大的点。所以，我们只需求出中心，在求出中心到B点的距离即可解决本题。该算法的时间复杂度是O（N+Q）或O（（N+Q）*LogN）的。

这题很像紧急集合那道题
询问树上的一个点到其他三个点的距离之和最短
两两lca 深度最大的即为答案

或者也可以分类讨论
假如z在xy与lca的路径之外 答案为lca到z的路径距离
假如z在xy与lca的路径之中 答案为lca到z的路径距离 答案为在这条路径上的点与z的lca到z的距离 可以通过dfs序列和倍增来实现

读题
文件
心态
空间
时间分配