分治法习题

Posted 2022-12-29 edviv

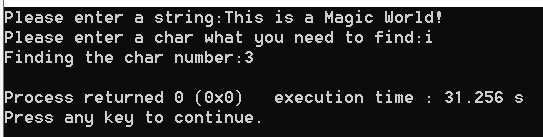
一.分治法设计一个算法，统计输入的非空字符串中给定字符的个数。

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <string.h>
 4 using namespace std;
 5 const int maxn = 1000;
 6 char str[maxn];
 7 char TargetChar;
 8 int CharNum;
 9 int CountTargetCharNum(char s[], char TargetChar, int begin, int end)
10 
11     int L, R;
12     if(begin == end) return (s[begin] == TargetChar);
13     else
14     
15         L = CountTargetCharNum(s, TargetChar, begin, begin + (end - begin)/2);
16         R = CountTargetCharNum(s, TargetChar, begin + (end - begin)/2 + 1, end);
17         return (L + R);
18     
19 
20 
21 int main()
22 
23     cout<<"Please enter a string:";
24     gets(str);
25     if(strlen(str) == 0)
26     
27         cout<<"Don‘t allow to enter a NULL string!"<<endl;
28         return 0;
29     
30     cout<<"Please enter a char what you need to find:";
31     cin>>TargetChar;
32     CharNum = CountTargetCharNum(str, TargetChar, 0, maxn - 1);
33     cout<<"Finding the char number:"<<CharNum<<endl;
34     return 0;
35 

二.非递归形式设计二分搜索程序。

 1 int BinarySearch(int ArrayData[], int x, int n)
 2 
 3     int L = 0, R = n - 1;
 4     while(L <= R)
 5     
 6         int mid = (L + R)/2;
 7         if(x == ArrayData[mid]) return mid;
 8         if(x > ArrayData[mid]) L = mid + 1;
 9         else R = mid - 1;
10     
11     return -1; //未找到 x
12 

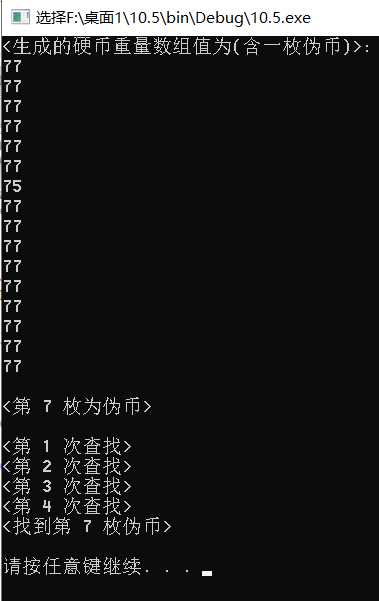
三.16个硬币放袋子里，其中有一枚硬币是假币，并且那个伪造的硬币比真币轻，设计一个算法找到那枚假币。

 1 #include <bits/stdc++.h>
 2 #define ARRAY_SIZE 16
 3 #define TRUE 1
 4 #define FALSE 0
 5 using namespace std;
 6 int CallTimes = 0;
 7 //生成包含 N 个硬币重量的数组(含一枚伪币)，并返回伪币位置
 8 int GreateRandomCoinWeightArray(int *p, int N)
 9 
10     int i, kt;
11     int TrueCoinWeight, FakeCoinWeight;
12     int IsStop;
13     //生成随机数种子
14     srand((unsigned)time(NULL));
15     //生成随机真币重量值(在 50 ~ 100 之间)
16     TrueCoinWeight = 50 + rand()%(100 - 50);
17     //生成随机伪币位置(在 0 ~ N - 1 之间)
18     kt = rand() % N;
19     //设置真币重量
20     for(i = 0; i < N; i++)
21         if(i != kt)
22             *(p + i) = TrueCoinWeight;
23     //生成一个比真币略轻的伪币重量
24     IsStop = FALSE;
25     while(!IsStop)
26     
27         FakeCoinWeight = 50 + rand()%(100 - 50);
28         //
29         if((TrueCoinWeight > FakeCoinWeight) && (TrueCoinWeight - FakeCoinWeight <= 5))
30         
31             IsStop = TRUE;
32             *(p + kt) = FakeCoinWeight;
33         
34     
35     //返回伪币位置
36     return kt;
37 
38 //计算数组中硬币的重量和
39 int CalcCoinTotalWeight(int ArrayData[], int kb, int ke)
40 
41     int i, TotalWeight = 0;
42     for(i = kb; i <= ke; i++) TotalWeight += ArrayData[i];
43     return TotalWeight;
44 
45 //采用分治法找到伪币(假定伪币一定存在且只有一枚)
46 //kb:(子)数组左边界( begin )
47 //ke:(子)数组右边界( end )
48 int FindFakeCoin(int ArrayData[], int kb, int ke)
49 
50     int LWeight, RWeight;
51     CallTimes++;
52     printf("<第 %d 次查找>\\n",CallTimes);
53     if((ke - kb) == 1)  //(子)数组中仅包含两个元素
54     
55         if(ArrayData[kb] < ArrayData[ke]) return kb;
56         else return ke;
57     
58     else //(子)数组中包含有多个元素
59     
60         //计算子数组硬币重量
61         LWeight = CalcCoinTotalWeight(ArrayData, kb, kb + (ke - kb)/2);  
62         RWeight = CalcCoinTotalWeight(ArrayData,kb + (ke - kb)/2 + 1, ke);
63         if(LWeight < RWeight)  //伪币在数组左半部分
64             return FindFakeCoin(ArrayData, kb, kb + (ke - kb)/2);
65         else      //伪币在数组右半部分
66             return FindFakeCoin(ArrayData, kb + (ke - kb)/2 + 1, ke);
67     
68 
69 int main()
70 
71     int ArrayData[ARRAY_SIZE];
72     int i, k, FakeCoinPos;
73     //生成包含 N 个硬币重量的数组(含一枚伪币),并返回伪币位置
74     k = GreateRandomCoinWeightArray(ArrayData, ARRAY_SIZE);
75     //输出随机数组内容
76     printf("<生成的硬币重量数组值为(含一枚伪币)>:\\n");
77     for(i = 0; i < ARRAY_SIZE; i++) printf("%d\\n",ArrayData[i]);
78     printf("\\n");
79     printf("<第 %d 枚为伪币>\\n",(k + 1));
80     printf("\\n");
81     //采用分治法找到伪币位置
82     FakeCoinPos = FindFakeCoin(ArrayData, 0, ARRAY_SIZE - 1);
83     printf("<找到第 %d 枚伪币>\\n",(FakeCoinPos+1));
84     printf("\\n");
85     //等待用户输入任意一键返回
86     system("PAUSE");
87     return 0;
88 

 

 

四. 大于 1 的正整数 n，设计一个算法计算 n 有多少种不同的分解式。

 1 int TotalModeNum = 0;
 2 int CalcIntDecomModeNum(int n)
 3 
 4     if(n == 1) TotalModeNum++;
 5     else
 6     
 7         for(int i = 2; i <= n; i++)
 8             if(n % i == 0)
 9                 CalcIntDecomModeNum(n/i);
10     
11 

五.给定 a, 分治法设计出 a^n 的算法

1 double CalcPow(double a, int n)
2 
3     if(n == 0) return 1.0;
4     double b = CalcPow(a, n/2);
5     b *= b;
6     if(n%2==1) b *= a;   // 处理奇数次幂的情况
7     return b;
8 

六.给定两个长度相等的数组，分治算法求出合并后的排序数组的中位数。

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <stdlib.h>
 4 #include <string.h>
 5 using namespace std;
 6 const int maxn = 1000;
 7 int a[maxn], b[maxn];
 8 int CalcMedian(int a[], int n)
 9 
10     if(n%2 == 0)
11         return (a[n/2] + a[n/2-1])/2;
12     else
13         return a[n/2];
14 
15 
16 int CalcArrayMedian(int A[], int B[], int n)
17 
18     int m1, m2;
19     if(n <= 0) return -1;
20     if(n == 1) return (A[0] + B[0])/2;
21     if(n == 2) return (max(A[0], B[0]) + min(A[1], B[1]))/2;
22 
23     m1 = CalcMedian(A, n);
24     m2 = CalcMedian(B, n);
25 
26     if(m1 == m2) return m1;
27     if(m1 < m2)
28     
29         if(n%2 == 0) return CalcArrayMedian(A + n/2 - 1, B, n/2 + 1);
30         else return CalcArrayMedian(A + n/2, B, n/2+1);
31     
32     else
33     
34         if(n%2 == 0) return CalcArrayMedian(B + n/2 - 1, A, n/2 + 1);
35         else return CalcArrayMedian(B + n/2, A, n/2 + 1);
36     
37 
38 int main()
39 
40     int m;
41     cin>>m;
42     for(int i = 0; i < m; i++) cin>>a[i];
43     for(int i = 0; i < m; i++) cin>>b[i];
44     int mid = CalcArrayMedian(a,b,m);
45     cout<<mid<<endl;
46     return 0;
47