类欧几里得模板 p5170

Posted 2022-12-29 pangbi

 

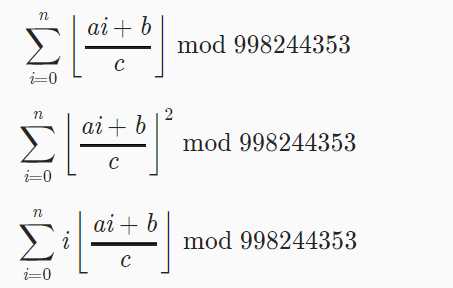
 1 //类欧几里得的模板题  p5170
 2 //求这三个式子；
 3 //第一个跟后两个没关联
 4 //后两个跟其余两个都有关联；
 5 
 6 
 7 #include<cstdio>
 8 #include<algorithm>
 9 #include<math.h>
10 #include<string.h>
11 using namespace std;
12 typedef long long ll;
13 const ll inv2=499122177;    
14 const ll inv6=166374059;
15 const ll mod=998244353;
16 int t;
17 ll n,a,b,c;
18 struct query
19 
20     ll f;
21     ll g;
22     ll h;
23 ;
24 query solve(ll a,ll b,ll c,ll n)
25 
26     query ans,prec;
27     if(a==0)
28         ans.f=(b/c)*(n+1)%mod;
29         ans.g=(b/c)*n%mod*(n+1)%mod*inv2%mod;
30         ans.h=(b/c)*(b/c)%mod*(n+1)%mod;
31     
32     else if(a>=c||b>=c)
33         prec=solve(a%c,b%c,c,n);
34         ans.f=(prec.f+n*(n+1)%mod*inv2%mod*(a/c)%mod+(n+1)*(b/c)%mod)%mod;
35         ans.g=((a/c)*n%mod*(n+1)%mod*(2*n+1)%mod*inv6%mod+
36                (b/c)*n%mod*(n+1)%mod*inv2%mod+prec.g)%mod;
37         ans.h=(prec.h+(a/c)*(a/c)%mod*n%mod*(n+1)%mod*(2*n+1)%mod*inv6%mod+
38                (n+1)*(b/c)%mod*(b/c)%mod+2*(a/c)%mod*prec.g%mod+
39                2*(b/c)%mod*prec.f%mod+2*(a/c)%mod*(b/c)%mod*n%mod*(n+1)%mod*inv2%mod)%mod;
40     
41     else
42         ll m=(a*n+b)/c;
43         prec=solve(c,c-b-1,a,m-1);
44         ans.f=(n*(m%mod)%mod-prec.f)%mod;
45         ans.g=(n*(n+1)%mod*(m%mod)%mod-prec.f-prec.h)%mod*inv2%mod;
46         ans.h =(n*(m%mod)%mod*((m+1)%mod)%mod-2*prec.g-2*prec.f-ans.f)%mod;
47     
48     return ans;
49 
50 int main()
51 
52     scanf("%d",&t);
53     while(t--)
54         scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
55         query ans=solve(a,b,c,n);
56         printf("%lld %lld %lld\\n", (ans.f + mod) % mod, (ans.h + mod) % mod, (ans.g + mod) % mod);
57     
58     return 0;
59 

求第一个式子的模板

 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<math.h>
 4 #include<string.h>
 5 using namespace std;
 6 typedef long long ll;
 7 const ll inv2=499122177;
 8 const ll inv6=166374059;
 9 const ll mod=998244353;
10 int t;
11 ll n,a,b,c;
12 ll solve(ll a,ll b,ll c,ll n)
13 
14     ll ans,prec;
15     if(a==0) ans=(b/c)*(n+1)%mod;
16     else if(a>=c||b>=c)
17         prec=solve(a%c,b%c,c,n);
18         ans=(prec+n*(n+1)%mod*inv2%mod*(a/c)%mod+(n+1)*(b/c)%mod)%mod;
19     
20     else
21         ll m=(a*n+b)/c;
22         prec=solve(c,c-b-1,a,m-1);
23         ans=(n*(m%mod)%mod-prec)%mod;
24     
25     return ans;
26 
27 int main()
28 
29     scanf("%d",&t);
30     while(t--)
31         scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
32         ll ans=solve(a,b,c,n);
33         printf("%lld",(ans+mod)%mod);
34     
35     return 0;
36