上节,我们学习了如何通过卷积网络实现滑动窗口对象检测算法,但效率很低。这节我们讲讲如何在卷积层上应用这个算法。
为了构建滑动窗口的卷积应用,首先要知道如何把神经网络的全连接层转化成卷积层。我们先讲解这部分内容,并演示卷积的应用过程。
一 卷积的滑动窗口实现
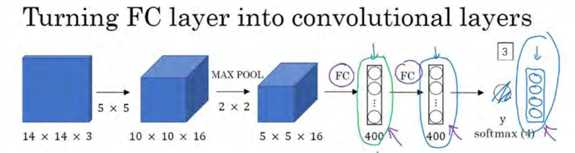
假设对象检测算法输入一个 14×14×3 的图像,图像很小,不过演示起来方便。在这里过滤器大小为 5×5,数量是 16, 14×14×3 的图像在过滤器处理之后映射为 10×10×16。然后通过参数为 2×2 的最大池化操作,图像减小到 5×5×16。然后添加一个连接 400 个单元的全连接层,接着再添加一个全连接层,最后通过 softmax 单元输出y。为了跟下图区分开,我先做一点改动,用 4 个数字来表示y,它们分别对应 softmax 单元所输出的 4 个分类出现的概率。这 4 个分类可以是行人、汽车、摩托车和背景或其它对象。
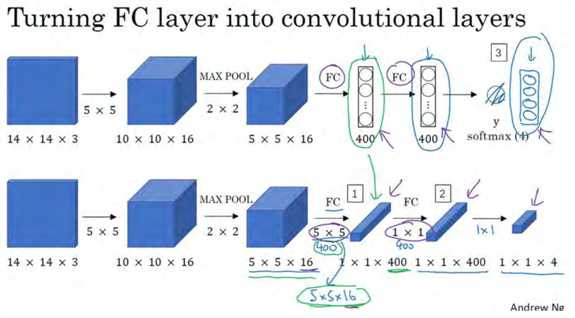
现在我要演示的就是如何把这些全连接层转化为卷积层,画一个这样的卷积网络,它的前几层和之前的一样,而对于下一层,也就是这个全连接层,我们可以用 5×5 的过滤器来实现,数量是 400 个(编号 1 所示),输入图像大小为 5×5×16,用 5×5 的过滤器对它进行卷积操作,过滤器实际上是 5×5×16,因为在卷积过程中,过滤器会遍历这 16 个通道,所以这两处的通道数量必须保持一致,输出结果为 1×1。假设应用 400 个这样的 5×5×16 过滤器,输出维度就是 1×1×400,我们不再把它看作一个含有 400 个节点的集合,而是一个 1×1×400的输出层。从数学角度看,它和全连接层是一样的,因为这 400 个节点中每个节点都有一个5×5×16 维度的过滤器,所以每个值都是上一层这些 5×5×16 激活值经过某个任意线性函数的输出结果。
我们再添加另外一个卷积层(编号 2 所示),这里用的是 1×1 卷积,假设有 400 个 1×1的过滤器,在这 400 个过滤器的作用下,下一层的维度是 1×1×400,它其实就是上个网络中的这一全连接层。最后经由 1×1 过滤器的处理,得到一个 softmax 激活值,通过卷积网络,我们最终得到这个 1×1×4 的输出层,而不是这 4 个数字(编号 3 所示)。
以上就是用卷积层代替全连接层的过程,结果这几个单元集变成了 1×1×400 和 1×1×4 的维度。
掌握了卷积知识,我们再看看如何通过卷积实现滑动窗口对象检测算法。
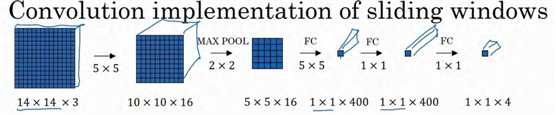
假设向滑动窗口卷积网络输入 14×14×3 的图片,为了简化演示和计算过程,这里我们依然用 14×14的小图片。和前面一样,神经网络最后的输出层,即 softmax单元的输出是 1×1×4,我画得比较简单,严格来说, 14×14×3 应该是一个长方体,第二个 10×10×16 也是一个长方体,但为了方便,我只画了正面。所以,对于 1×1×400 的这个输出层,我也只画了它 1×1 的那一面,所以这里显示的都是平面图,而不是 3D 图像。
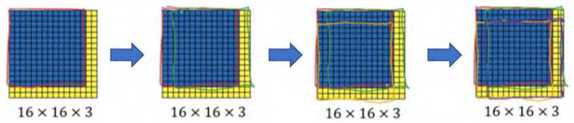
假设输入给卷积网络的图片大小是 14×14×3,测试集图片是 16×16×3,现在给这个输入图片加上黄色条块,在最初的滑动窗口算法中,你会把这片蓝色区域输入卷积网络(红色笔标记)生成 0 或 1 分类。接着滑动窗口,步幅为 2 个像素,向右滑动 2 个像素,将这个绿框区域输入给卷积网络, 运行整个卷积网络,得到另外一个标签 0 或 1。继续将这个橘色区域输入给卷积网络,卷积后得到另一个标签,最后对右下方的紫色区域进行最后一次卷积操作。我们在这个 16×16×3 的小图像上滑动窗口,卷积网络运行了 4 次,于是输出了了 4 个标签。
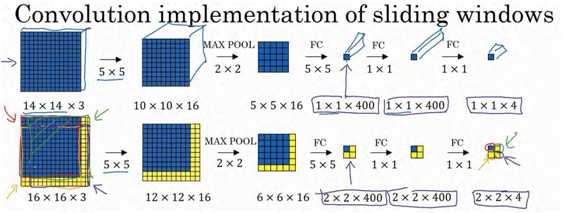
结果发现,这 4 次卷积操作中很多计算都是重复的。所以执行滑动窗口的卷积时使得卷积网络在这 4 次前向传播过程中共享很多计算,尤其是在这一步操作中(编号 1),卷积网络运行同样的参数,使得相同的 5×5×16 过滤器进行卷积操作,得到 12×12×16 的输出层。然后执行同样的最大池化(编号 2) ,输出结果 6×6×16。照旧应用 400 个 5×5 的过滤器(编号3),得到一个 2×2×400 的输出层,现在输出层为 2×2×400,而不是 1×1×400。应用 1×1 过滤器(编号 4)得到另一个 2×2×400 的输出层。再做一次全连接的操作(编号 5),最终得到2×2×4 的输出层,而不是 1×1×4。最终,在输出层这 4 个子方块中,蓝色的是图像左上部分14×14 的输出(红色箭头标识),右上角方块是图像右上部分(绿色箭头标识)的对应输出,左下角方块是输入层左下角(橘色箭头标识),也就是这个 14×14 区域经过卷积网络处理后的结果,同样,右下角这个方块是卷积网络处理输入层右下角 14×14 区域(紫色箭头标识)的结果。
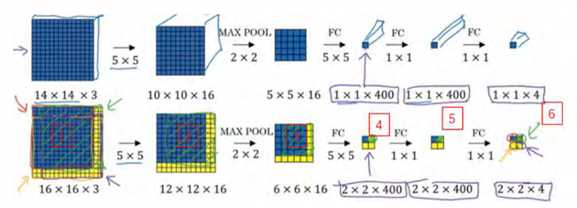
如果你想了解具体的计算步骤,以绿色方块为例,假设你剪切出这块区域(编号 1),传递给卷积网络,第一层的激活值就是这块区域(编号 2),最大池化后的下一层的激活值是这块区域(编号 3),这块区域对应着后面几层输出的右上角方块(编号 4, 5, 6)。
所以该卷积操作的原理是我们不需要把输入图像分割成四个子集,分别执行前向传播,而是把它们作为一张图片输入给卷积网络进行计算,其中的公共区域可以共享很多计算,就像这里我们看到的这个 4 个 14×14 的方块一样。

下面我们再看一个更大的图片样本,假如对一个 28×28×3 的图片应用滑动窗口操作,如果以同样的方式运行前向传播,最后得到 8×8×4 的结果。跟上一个范例一样,以 14×14 区域滑动窗口,首先在这个区域应用滑动窗口,其结果对应输出层的左上角部分。接着以大小为2 的步幅不断地向右移动窗口,直到第 8 个单元格,得到输出层的第一行。然后向图片下方移动,最终输出这个 8×8×4 的结果。因为最大池化参数为 2,相当于以大小为 2 的步幅在原始图片上应用神经网络。

总结一下滑动窗口的实现过程,在图片上剪切出一块区域,假设它的大小是 14×14,把它输入到卷积网络。继续输入下一块区域,大小同样是 14×14,重复操作,直到某个区域识别到汽车。
但是正如在前一页所看到的,我们不能依靠连续的卷积操作来识别图片中的汽车,比如,我们可以对大小为 28×28 的整张图片进行卷积操作,一次得到所有预测值,如果足够幸运,神经网络便可以识别出汽车的位置。

以上就是在卷积层上应用滑动窗口算法的内容,它提高了整个算法的效率。不过这种算法仍然存在一个缺点,就是边界框的位置可能不够准确。下面,我们将学习如何解决这个问题。
二 Bounding Box 预测
上面,你们学到了滑动窗口法的卷积实现,这个算法效率更高,但仍然存在问题,不能输出最精准的边界框。在这里,我们看看如何得到更精准的边界框。

在滑动窗口法中,你取这些离散的位置集合,然后在它们上运行分类器,在这种情况下,这些边界框没有一个能完美匹配汽车位置,也许这个框(编号 1)是最匹配的了。还有看起来这个真实值,最完美的边界框甚至不是方形,稍微有点长方形(红色方框所示),长宽比有点向水平方向延伸,有没有办法让这个算法输出更精准的边界框呢?
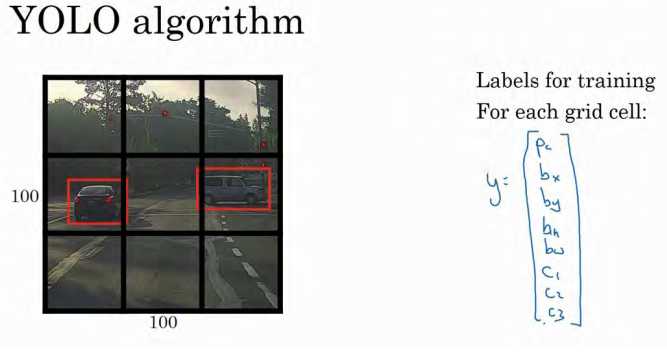
其中一个能得到更精准边界框的算法是 YOLO 算法, YOLO(You only look once)意思是你只看一次,这是由 Joseph Redmon, Santosh Divvala, Ross Girshick 和 Ali Farhadi 提出的算法。
是这么做的,比如你的输入图像是 100×100 的,然后在图像上放一个网格。为了介绍起来简单一些,我用 3×3 网格,实际实现时会用更精细的网格,可能是 19×19。基本思路是使用图像分类和定位算法,前面介绍过的,然后将算法应用到 9 个格子上。(基本思路是,采用图像分类和定位算法,逐一应用在图像的 9 个格子中。)更具体一点,你需要这样定义训练标签,所以对于 9 个格子中的每一个指定一个标签y,y是 8 维的,和你之前看到的一样。
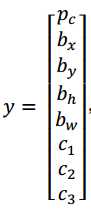
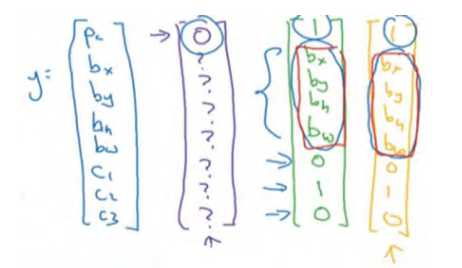
pc等于 0 或 1 取决于这个绿色格子中是否有图像。然后bx、by、b?和bw作用就是,如果那个格子里有对象,那么就给出边界框坐标。然后c1、c2和c3就是你想要识别的三个类别,背景类别不算,所以你尝试在背景类别中识别行人、汽车和摩托车,那么1、c2和c3可以是行人、汽车和摩托车类别。这张图里有 9 个格子,所以对于每个格子都有这么一个向量。

我们看看左上方格子,这里这个(编号 1),里面什么也没有,所以左上格子的标签向量y是:
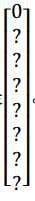
然后这个格子(编号 2)的输出标签y也是一样,这个格子(编号 3),还有其他什么也没有的格子都一样。
现在这个格子呢?讲的更具体一点,这张图有两个对象, YOLO 算法做的就是,取两个对象的中点,然后将这个对象分配给包含对象中点的格子。所以左边的汽车就分配到这个格子上(编号 4),然后这辆 Condor(车型:神鹰)中点在这里,分配给这个格子(编号 6)。所以即使中心格子(编号 5)同时有两辆车的一部分,我们就假装中心格子没有任何我们感兴趣的对象,所以对于中心格子,分类标签 y 和这个向量类似,和这个没有对象的向量类似,即:
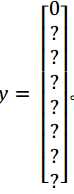
而对于这个格子,这个用绿色框起来的格子(编号 4),目标标签就是这样的,这里有一个对象,pc= 1,然后你写出bx、by、b?和bw来指定边界框位置,然后还有类别 1是行人,那么c1 = 0,类别 2 是汽车,所以c2 = 1,类别3是摩托车,则数值c3 = 0,即y为:
![]()
右边这个格子(编号 6)也是类似的,因为这里确实有一个对象,它的向量应该是这个样子的:
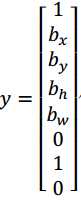
所以对于这里 9 个格子中任何一个,你都会得到一个 8 维输出向量,因为这里是 3×3 的网格,所以有 9 个格子,总的输出尺寸是 3×3×8,所以目标输出是 3×3×8。因为这里有 3×3格子,然后对于每个格子,你都有一个 8 维向量y,所以目标输出尺寸是 3×3×8。
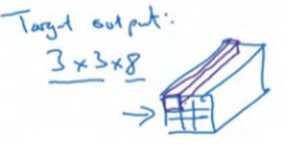
对于这个例子中,左上格子是 1×1×8,对应的是 9 个格子中左上格子的输出向量。所以对于这 3×3 中每一个位置而言,对于这 9 个格子,每个都对应一个 8 维输出目标向量y,其中一些值可以是 dont care-s(即?),如果这里没有对象的话。所以总的目标输出,这个图片的输出标签尺寸就是 3×3×8。
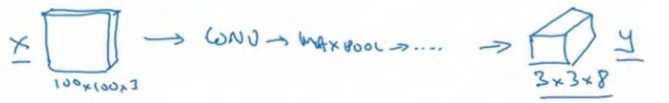
如果你现在要训练一个输入为 100×100×3 的神经网络,现在这是输入图像,然后你有一个普通的卷积网络,卷积层,最大池化层等等,最后你会有这个,选择卷积层和最大池化层,这样最后就映射到一个 3×3×8 输出尺寸。所以你要做的是,有一个输入x,就是这样的输入图像,然后你有这些 3×3×8 的目标标签y。当你用反向传播训练神经网络时,将任意输入x映射到这类输出向量y。
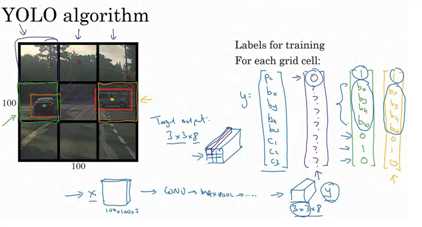
所以这个算法的优点在于神经网络可以输出精确的边界框,所以测试的时候,你做的是喂入输入图像x,然后跑正向传播,直到你得到这个输出y。然后对于这里 3×3 位置对应的 9个输出,我们在输出中展示过的,你就可以读出 1 或 0(编号 1 位置),你就知道 9 个位置之一有个对象。如果那里有个对象,那个对象是什么(编号 3 位置),还有格子中这个对象的边界框是什么(编号 2 位置)。只要每个格子中对象数目没有超过 1 个,这个算法应该是没问题的。一个格子中存在多个对象的问题,我们稍后再讨论。但实践中,我们这里用的是比较小的 3×3 网格,实践中你可能会使用更精细的 19×19 网格,所以输出就是 19×19×8。这样的网格精细得多,那么多个对象分配到同一个格子得概率就小得多。
重申一下,把对象分配到一个格子的过程是,你观察对象的中点,然后将这个对象分配到其中点所在的格子,所以即使对象可以横跨多个格子,也只会被分配到 9 个格子其中之一,就是 3×3 网络的其中一个格子,或者 19×19 网络的其中一个格子。在 19×19 网格中,两个对象的中点(图中蓝色点所示)处于同一个格子的概率就会更低。
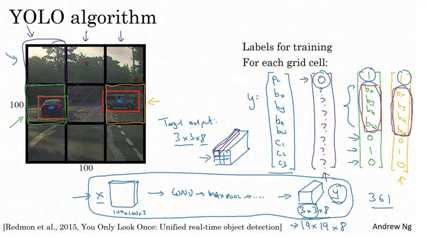
所以要注意,首先这和图像分类和定位算法非常像,我们在之前讲过的,就是它显式地输出边界框坐标,所以这能让神经网络输出边界框,可以具有任意宽高比,并且能输出更精确的坐标,不会受到滑动窗口分类器的步长大小限制。其次,这是一个卷积实现,你并没有在 3×3 网格上跑 9 次算法,或者,如果你用的是 19×19 的网格, 19 平方是 361 次,所以你不需要让同一个算法跑 361 次。相反,这是单次卷积实现,但你使用了一个卷积网络,有很多共享计算步骤,在处理这 3×3 计算中很多计算步骤是共享的,或者你的 19×19 的网格,所以这个算法效率很高。
事实上 YOLO 算法有一个好处,也是它受欢迎的原因,因为这是一个卷积实现,实际上它的运行速度非常快,可以达到实时识别。在结束之前我还想给你们分享一个小细节,如何编码这些边界框bx、by、b?和bw,我们在后面讨论。
这里有两辆车,我们有个 3×3 网格,我们以右边的车为例(编号 1),红色格子里有个对象,所以目标标签y就是,pc= 1,然后bx、by、b?和bw,然后c1 = 0,c2 = 1,c3 = 0,即
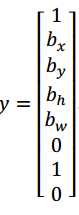
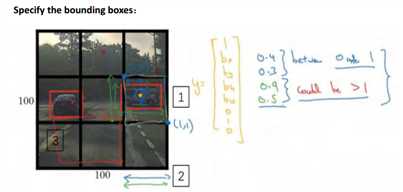
在 YOLO 算法中,对于这个方框(编号 1 所示),我们约定左上这个点是(0,0),然后右下这个点是(1,1),要指定橙色中点的位置,bx大概是 0.4,因为它的位置大概是水平长度的0.4,然后by大概是 0.3,然后边界框的高度用格子总体宽度的比例表示,所以这个红框的宽度可能是蓝线(编号 2 所示的蓝线)的 90%,所以bh是 0.9,它的高度也许是格子总体高度的一半,这样的话bw就是 0.5。换句话说, bx、by、b?和bw单位是相对于格子尺寸的比列,所以bx和by必须在 0 和 1 之间,因为从定义上看,橙色点位于对象分配到格子的范围内,如果它不在 0 和 1 之间,如果它在方块外,那么这个对象就应该分配到另一个格子上。这个值(bh和bw)可能会大于 1,特别是如果有一辆汽车的边界框是这样的(编号 3 所示),那么边界框的宽度和高度有可能大于 1。
指定边界框的方式有很多,但这种约定是比较合理的,如果你去读 YOLO 的研究论文,YOLO 的研究工作有其他参数化的方式,可能效果会更好,我这里就只给出了一个合理的约定,用起来应该没问题。不过还有其他更复杂的参数化方式,涉及到 sigmoid 函数,确保这个值(bx和by)介于0和1之间,然后使用指数参数化来确保这些(bh和bw)都是非负数,这个必须大于等于 0。还有其他更高级的参数化方式,可能效果要更好一点,但我这里讲的办法应该是管用的。