每日一题_191004

Posted 2022-12-19 math521

三个顶点均在椭圆上的三角形称为椭圆的内接三角形,已知点\\(A\\)是椭圆的一个短轴端点,如果以\\(A\\)为直角顶点的椭圆内接等腰直角三角形有且仅有三个,则椭圆的离心率的取值范围是\\(\\underline\\qquad\\qquad\\).
解析: \\(\\triangle ABC\\)与椭圆如图所示,不妨设椭圆方程为\\[ \\dfracx^2a^2+\\dfracy^2b^2=1,a>b>0.\\]

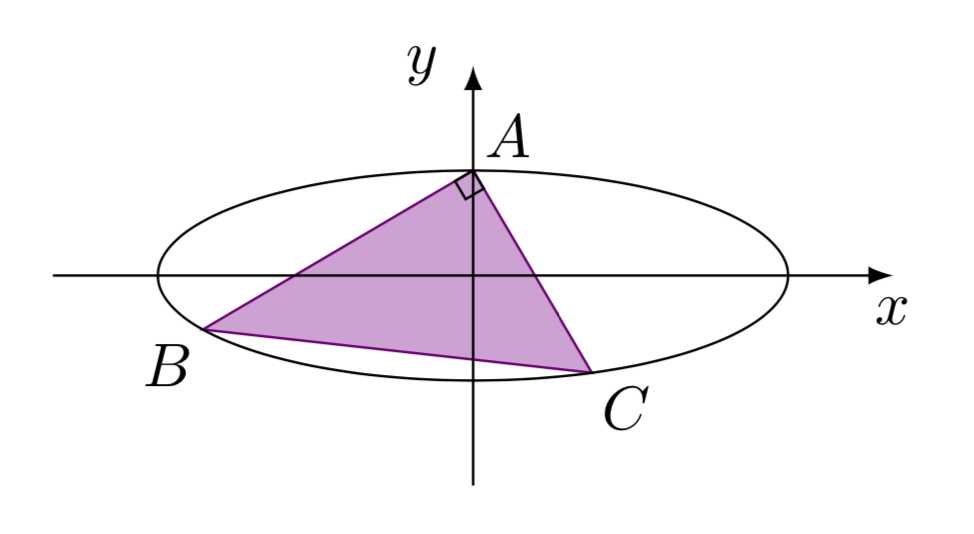
因此原椭圆在新坐标系下的直角坐标方程为\\[\\dfracx^2a^2+\\dfracy^2b^2+\\dfrac2yb=0.\\qquad (\\ast)\\]建立以新坐标系坐标原点\\(O\\)为极点,以新坐标系的\\(x\\)轴的正半轴为极轴的极坐标系,设\\[\\angle CAx=\\theta,\\theta\\in\\left(0,\\dfrac\\pi2\\right).\\]则\\(C,B\\)点的极坐标可设为\\[C\\left(\\rho_1,2\\pi-\\theta\\right),B\\left(\\rho_2,2\\pi-\\theta-\\dfrac\\pi2\\right),\\]则\\(C\\)的直角坐标可表示为\\[C\\left(\\rho_1 \\cos\\theta,-\\rho_1 \\sin\\theta\\right),B\\left(-\\rho_2 \\sin\\theta,-\\rho_2 \\cos\\theta\\right)\\]将\\(C,B\\)两点坐标分别代入方程\\((\\ast)\\),并整理可得\\[ \\rho_1=\\dfrac\\dfrac2\\sin\\thetab\\dfrac\\cos^2\\thetaa^2+\\dfrac\\sin^2\\thetab^2,\\rho_2=\\dfrac\\dfrac2\\cos\\thetab\\dfrac\\sin^2\\thetaa^2+\\dfrac\\cos^2\\thetab^2.\\]结合\\(\\rho_1=\\rho_2\\)可得关于\\(\\theta\\)的方程\\[ \\dfracb^2a^2\\tan^3\\theta-\\tan^2\\theta+\\tan\\theta-\\dfracb^2a^2=0,\\theta\\in\\left(0,\\dfrac\\pi2\\right).\\]
题意即关于\\(\\tan\\theta\\)的方程有三个解,易求得\\(\\dfracb^2a^2\\)的取值范围为\\(\\left(0,\\dfrac13\\right)\\),因此所求离心率的取值范围为\\(\\left(\\dfrac\\sqrt63,1\\right)\\).