函数的迭代

Posted 2022-12-18 wanghai0666

前言

典例剖析

例1【2018凤翔中学高三文科数学冲刺模拟第10套第8题】已知\\(f(x)=\\begincases1，&x\\in[0，1]\\\\x-3，&x\\notin[0，1]\\endcases\\)，则使得\\(f(f(x))=1\\)成立的\\(x\\)的取值范围是【】

$A.[0，1]$ $B.[0，1]\\cup\\7\\$ $C.[0，1]\\cup [3，4]$ $D.[0，1]\\cup[3，4]\\cup\\7\\$

分析：本题目属于求解分段函数方程，可以将\\(f(x)\\)这个整体视为已知中的\\(x\\)，则原分段函数方程等价于

第一种情形，\\(0\\leq f(x)\\leq 1\\)且\\(f(x)=1\\)；或第二种情形，\\(f(x)-3=1\\)且\\(f(x)\\notin[0，1]\\)，

其中第一种可化简为\\(0\\leq f(x)\\leq 1\\)，再等价转化为\\(\\begincasesx\\in[0，1]\\\\f(x)=1\\endcases\\)或\\(\\begincasesx\\notin[0，1]\\\\0\\leq x-3\\leq 1\\endcases\\)

解得\\(0\\leq x\\leq 1\\)或\\(3\\leq x\\leq 4\\)；

第二种可化简为\\(f(x)=4\\)，再等价转化为\\(\\begincasesx\\in[0，1]\\\\1=4\\endcases\\)或\\(\\begincasesx\\notin[0，1]\\\\x-3=4\\endcases\\)，解得\\(x=7\\)；

综上所述，\\(x\\)的取值范围是\\([0，1]\\cup[3，4]\\cup\\7\\\\)，故选\\(D\\)。

例1已知函数\\(f(x)\\)是定义在\\(R\\)上的奇函数，当\\(x<0\\)时，\\(f(x)=(x+1)e^x\\)，则对任意的\\(m\\in R\\)，函数\\(F(x)=\\) \\(f[f(x)]-m\\)的零点至多有【】个。

$A.3$ $B.4$ $C.6$ $D.9$

【法1】：利用复合函数的图像解决问题；首先利用函数的奇偶性求出函数\\(f(x)\\)的解析式；

题目给定了\\(x<0\\)时的解析式，则当\\(x>0\\)时，\\(-x<0\\)，则\\(f(-x)=(-x+1)e^-x\\)，

又函数\\(f(x)\\)为奇函数，则\\(f(x)=-f(-x)=-(-x+1)e^-x=(x-1)e^-x\\)，又\\(f(0)=0\\)，

故函数的解析式为\\(f(x)=\\left\\\\beginarrayl(x+1)e^x，x<0\\\\0，x=0\\\\(x-1)e^-x，x>0\\endarray\\right.\\)

接下来利用导数先研究\\(x<0\\)时的单调性，\\(f(x)=(x+1)e^x\\)，则\\(f'(x)=(x+2)e^x\\)，

则\\(x\\in (-\\infty，-2)\\)时，函数\\(f(x)\\)单调递减，\\(x\\in (2，0)\\)时，函数\\(f(x)\\)单调递增，又\\(f(0)=1\\)，

故结合单调性和奇偶性，做出\\(R\\)上的函数示意图如下：

接下来分析复合函数\\(h(x)=f[f(x)]\\)的图像。

当\\(x=0\\)时，\\(f(0)=0\\)时，\\(f(f(0))=0\\)；

当\\(x\\in (0，1)\\)时，内函数\\(f(x)\\)单调递增，且\\(f(x)\\in (-1，0)\\)，此时外函数在\\((-1，0)\\)上也单调递增，故\\(f(f(x))\\)在\\(x\\in (0，1)\\)上单调递增；

当\\(x=1\\)时，\\(f(1)=0\\)，\\(f(f(1))=0\\)；

当\\(x\\in (1，2)\\)时，内函数\\(f(x)\\)单调递增，且\\(f(x)\\in (0，e^-2)\\)，此时外函数在\\((0，e^-2)\\)上也单调递增，故\\(f(f(x))\\)在\\(x\\in (1，2)\\)上单调递增，且函数值从\\(1\\)逐渐增大到\\(f(f(2))\\)且\\(f(f(2))<0\\)；

当\\(x\\in (2，+\\infty)\\)时，内函数\\(f(x)\\)单调递减，且\\(f(x)\\in (0，e^-2)\\)，此时外函数在\\((0，e^-2)\\)上单调递增，故\\(f(f(x))\\)在\\(x\\in (2，+\\infty)\\)上单调递减，且函数值逐渐趋近于\\(-1\\)；

然后，用奇函数的性质对称画出\\(x<0\\)的那一部分，总体图像如下图所示；

由图可知，函数\\(y=f(f(x))\\)和\\(y=m\\)的交点最多有三个，故选\\(A\\)；

• 下述的解法2，最好先说明借助图像如何由\\(x\\)找\\(f(x)\\)，以及由\\(f(x)\\)找\\(x\\)；只要双向的对应理解透彻，下述的解法就好思考多了；

【法2】：由外向里，从函数值找自变量，首先利用函数的奇偶性求出函数\\(f(x)\\)的解析式；

题目给定了\\(x<0\\)时的解析式，则当\\(x>0\\)时，\\(-x<0\\)，则\\(f(-x)=(-x+1)e^-x\\)，

又函数\\(f(x)\\)为奇函数，则\\(f(x)=-f(-x)=-(-x+1)e^-x=(x-1)e^-x\\)，又\\(f(0)=0\\)，

故函数的解析式为\\(f(x)=\\left\\\\beginarrayl(x+1)e^x，x<0\\\\0，x=0\\\\(x-1)e^-x，x>0\\endarray\\right.\\)

接下来利用导数先研究\\(x<0\\)时的单调性，\\(f(x)=(x+1)e^x\\)，则\\(f'(x)=(x+2)e^x\\)，

则\\(x\\in (-\\infty，-2)\\)时，函数\\(f(x)\\)单调递减，\\(x\\in (2，0)\\)时，函数\\(f(x)\\)单调递增，又\\(f(0)=1\\)，

故结合单调性和奇偶性，做出\\(R\\)上的函数示意图如下：

令\\(F(x)=0\\)，即\\(f(f(x))=m\\)，由图可知，要使得函数\\(y=f(f(x))\\)与\\(y=m\\)的图像有交点，则\\(m\\in (-1，1)\\)；接下来关于\\(m\\)的取值分类讨论如下：

当\\(m\\in (0，e^-2)\\)时，如图所示，内函数\\(f(x)=a，a\\in (-1，0)\\)或\\(f(x)=b，b\\in (1，2)\\)或\\(f(x)=c，c\\in (2，+\\infty)\\)

若\\(f(x)=b\\)或\\(f(x)=c\\)时，不存在\\(x\\)；注意应该是在\\(y\\)轴上找点\\((0，b)\\)，然后过此点做\\(x\\)轴的平行线，显然和函数的图像没有交点；

若\\(f(x)=a， a\\in (-1，0)\\)时，此时和函数的图像最多有三个交点；

当\\(m\\in (e^-2，1)\\)时，内函数\\(f(x)=a，a\\in (-1，0)\\)，此时\\(f(x)\\in (-1，0)\\)时，函数\\(y=a\\)和函数\\(y=f(x)\\)图像最多有三个交点，

同理，当\\(m\\in (-e^-2，0)\\)或\\(m\\in (-1，-e^-2)\\)时，仿上说明，同样最多有三个交点，故选\\(A\\)；

例2【2019届高三理科数学资料用题】【2018日照一模】已知函数\\(f(x)=\\left\\\\beginarrayl|lgx|，x>0\\\\2^|x|，x\\leq 0\\endarray\\right.\\)，则函数\\(y=2f^2(x)\\) \\(-3f(x)\\) \\(+1\\)的零点个数是______个。

分析：函数\\(y=2f^2(x)-3f(x)+1\\)的零点个数即方程\\(2f^2(x)-3f(x)+1=0\\)的根的个数，

故先求解方程\\(2f^2(x)-3f(x)+1=0\\)，即\\([2f(x)-1][f(x)-1]=0\\)，

解得\\(f(x)=1\\)或\\(f(x)=\\cfrac12\\)，

接下来原方程的根的个数转化为方程\\(f(x)=1\\)或\\(f(x)=\\cfrac12\\)的根的个数，

故做出函数\\(y=f(x)\\)的图像和直线\\(y=1\\)和\\(y=\\cfrac12\\)，

由图像可以看出，其共有\\(5\\)个交点，故原函数的零点个数为\\(5\\)个。

例3【2019届高三理科数学三轮模拟用题】函数\\(f(x)=\\left\\\\beginarrayllog_2x，x>0\\\\x^2+4x+1，x<0\\endarray\\right.\\)，若实数\\(a\\)满足\\(f(f(a))=1\\)，则实数\\(a\\)的所有取值的和为___________。

法1：从数的角度入手思考，将内函数\\(f(x)\\)理解为整体，则\\(f(f(a))=1\\)等价于以下的两个方程组，

Ⅰ.\\(\\left\\\\beginarraylf(a)>0\\\\log_2f(a)=1\\endarray\\right.\\)，或者Ⅱ.\\(\\left\\\\beginarraylf(a)\\leq 0\\\\[f(a)]^2+4[f(a)]+1=1\\endarray\\right.\\)，

解Ⅰ得到，\\(f(a)=2\\)①；解Ⅱ得到，\\(f(a)=0\\)②或者\\(f(a)=-4\\)③；

再次求解①得到，\\(\\left\\\\beginarrayla>0\\\\log_2a=2\\endarray\\right.\\)，或\\(\\left\\\\beginarrayla\\leq 0\\\\a^2+4a+1=2\\endarray\\right.\\)，

解得\\(a=4\\)或\\(a=-2-\\sqrt5\\)，

求解②得到，\\(\\left\\\\beginarrayla>0\\\\log_2a=0\\endarray\\right.\\)，或\\(\\left\\\\beginarrayla\\leq 0\\\\a^2+4a+1=0\\endarray\\right.\\)，

解得\\(a=1\\)或\\(a=-2\\pm \\sqrt3\\)，

求解③得到，\\(\\left\\\\beginarrayla>0\\\\log_2a=-4\\endarray\\right.\\)，或\\(\\left\\\\beginarrayla\\leq 0\\\\a^2+4a+1=-4\\endarray\\right.\\)，

解得\\(a=\\cfrac116\\)或\\(a\\in \\varnothing\\)，

故实数\\(a\\)的所有取值的和为\\(4-2-\\sqrt5+1-2-\\sqrt3-2+\\sqrt3+\\cfrac116=-\\cfrac1516-\\sqrt5\\)。

法2：从图像入手分析，待编辑。

例4【2020届高三文科数学周末训练2用题】若函数\\(f(x)=\\left\\\\beginarraylx+1，x\\leqslant 0\\\\lnx，x>0，\\endarray\\right.\\) 则函数\\(y=f[f(x)]+1\\)的零点的个数为______ 个。

分析：首先学习理解一个分段函数方程的模型；

模型【求解分段函数方程】【2016第三次全国大联考第15题】已知\\(f(x)\\)是定义在R上的奇函数，且当\\(x<0\\)时，\\(f(x)=2x-1\\)，若\\(f(a)=3\\)，求实数\\(a\\)的值。

分析：先由奇偶性求得\\(x>0\\)时，\\(f(x)=2x+1\\)，

即得到函数的解析式为\\(f(x)=\\begincases2x-1&x<0\\\\0&x=0\\\\2x+1&x>0\\endcases\\)，且已知\\(f(a)=3\\)，求\\(a\\)的值，

等价转化为三个不等式组 \\(\\begincasesa<0\\\\2a-1=3\\endcases\\)，或\\(\\begincasesa=0\\\\0=3\\endcases\\)，或\\(\\begincasesa>0\\\\2a+1=3\\endcases\\)，

解得\\(a=1\\)。

学习理解透彻了上述模型后，我们开始求解本题目：

【法1】：从数的角度求解；令\\(f(x)=t\\)，则函数的零点问题转化为方程\\(f(t)=-1\\)的解的个数问题；

即相当于已知\\(f(x)=\\left\\\\beginarraylx+1，x\\leqslant 0\\\\lnx，x>0，\\endarray\\right.\\) 且\\(f(t)=-1\\)，求\\(t\\)的值；

则上述分段函数方程等价于\\(\\left\\\\beginarraylt\\leqslant 0\\\\t+1=-1\\endarray\\right.\\) 或\\(\\left\\\\beginarraylt> 0\\\\lnt=-1\\endarray\\right.\\)

解得\\(t=-2\\)或者\\(t=\\cfrac1e\\)，即\\(f(x)=-2\\)或者\\(f(x)=\\cfrac1e\\)，到此题目又可以转化为

已知\\(f(x)=\\left\\\\beginarraylx+1，x\\leqslant 0\\\\lnx，x>0，\\endarray\\right.\\) 且\\(f(x)=-2\\)，求\\(x\\)的值；可以仿上求解得到\\(2\\)个\\(x\\)的值；

或已知\\(f(x)=\\left\\\\beginarraylx+1，x\\leqslant 0\\\\lnx，x>0，\\endarray\\right.\\) 且\\(f(x)=\\cfrac1e\\)，求\\(x\\)的值；亦可以仿上求解得到\\(2\\)个\\(x\\)的值；

故所求的零点的个数为\\(4\\)个。

【法2】：从形的角度求解；先做出分段函数图像如下：

先将函数的零点问题转化为方程\\(f[f(x)]=-1\\)的根的个数问题；作直线\\(y=-1\\)与函数\\(y=f(x)\\)图像有两个交点，其横坐标分别为\\(x=-2\\)和\\(x=\\cfrac1e\\)，

然后在同样的图上，再分别作直线\\(y=-2\\)和\\(y=\\cfrac1e\\)，可以看出，这两条直线分别和分段函数\\(y=f(x)\\)有两个交点，故共有四个交点。即所求的零点的个数为\\(4\\)个。

例11设函数\\(f(x)=\\begincasesx^2+x,&x<0\\\\-x^2,&x\\ge 0 \\endcases\\)，若\\(f(f(a))\\leq 2\\)，则实数\\(a\\)的取值范围是_____.

法1：若能将\\(f(a)\\)理解成已知函数的\\(x\\)，

则可以将\\(f(f(a))\\leq 2\\)等价转化为以下的两个不等式组：

\\(\\begincases&f(a)<0\\\\&f^2(a)+f(a)\\leq 2 \\endcases\\) 或 \\(\\begincases&f(a)\\ge0\\\\&-f^2(a)\\leq 2 \\endcases\\)

分别解得：\\(-2\\leq f(a)<0\\)或\\(f(a)\\ge 0\\)，故\\(f(a)\\ge -2\\)；

到此问题转化为已知\\(f(x)=\\begincasesx^2+x,&x<0\\\\-x^2,&x\\ge 0 \\endcases\\)，\\(f(a)\\ge -2\\)，

求实数\\(a\\)的取值范围，这就容易多了。

再次转化为\\(\\begincases&a<0\\\\&a^2+a\\ge -2 \\endcases\\) 或 \\(\\begincases&a\\ge0\\\\&-a^2\\ge -2 \\endcases\\)

分别解得：\\(a<0\\)或\\(0\\leq a\\leq \\sqrt2\\)，故实数\\(a\\)的取值范围为\\((-\\infty，+\\sqrt2]\\)。

解后反思：本题经过两次抽丝剥茧般的处理，第一次的结果得到\\(f(a)\\ge -2\\)，

第二次的结果得到\\(a\\in (-\\infty，+\\sqrt2]\\)。

法2：图像法

自行做出函数图像，结合图像可知，

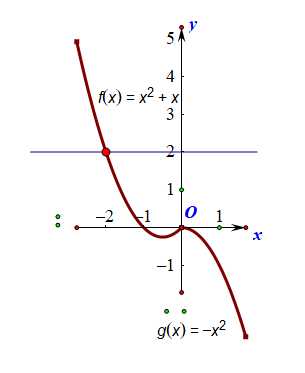
要使得\\(f(f(a))\\leq 2\\)，则必须\\(f(a)\\ge -2\\)，

这时就转化为分段函数不等式问题了。

\\(f(a)\\ge -2\\)等价于以下两个不等式组：

\\(\\begincases&a<0 \\\\&a^2+a\\ge -2\\endcases\\)或\\(\\begincases&a\\ge 0 \\\\&-a^2\\ge -2\\endcases\\)。

解得\\(a<0\\)或\\(0\\leq a\\leq \\sqrt2\\)，

故\\(a\\in(-\\infty，\\sqrt2]\\)。

例9已知函数\\(y=f(x)\\)和\\(y=g(x)\\)在\\([-2，2]\\)上的图像如图所示，给出下列四个命题：

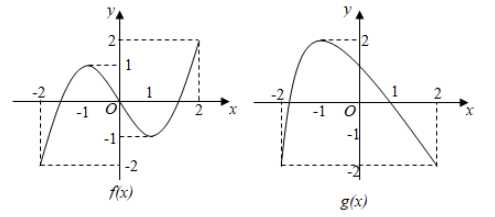
①方程\\(f[g(x)]=0\\)有且仅有\\(6\\)个根；②方程\\(g[f(x)]=0\\)有且仅有\\(3\\)个根；

③方程\\(f[f(x)]=0\\)有且仅有\\(5\\)个根；④方程\\(g[g(x)]=0\\)有且仅有\\(4\\)个根；

则正确的命题有 _______________。①③④

【法1】：从里向外分析，重新配图；得空整理；

对于命题①而言，复合函数为\\(f[g(x)]\\)；为什么如下选择区间？理由¹

在\\([-2，x_0]\\)上，\\(f[g(x)]\\nearrow\\)，\\(f[g(-2)]=f(-2)=-2\\)，\\(f[g(x_0)]=f(-1)=1\\)，其中\\(g(x_0)=-1\\);

在\\([x_0，x_1]\\)上，\\(f[g(x)]\\searrow\\)，\\(f[g(x_1)]=f(0)=0\\)，其中\\(g(x_1)=0\\)；

在\\([x_1，x_2]\\)上，\\(f[g(x)]\\searrow\\)，\\(f[g(x_2)]=f(1)=-1\\)，其中\\(g(x_2)=1\\)；

在\\([x_2，-1]\\)上，\\(f[g(x)]\\nearrow\\)，\\(f[g(-1)]=f(2)=2\\)；

在\\([-1，0]\\)上，\\(f[g(x)]\\searrow\\)，\\(f[g(0)]=f(1)=-1\\)；图中未说明，假定\\(g(0)=1\\);

在\\([0，1]\\)上，\\(f[g(x)]\\nearrow\\)，\\(f[g(1)]=f(-0.3)=0.4\\)；\\(g(1)=-0.3\\)，\\(f(-0.3)=0.4\\)为估算值；

在\\([1，x_3]\\)上，\\(f[g(x)]\\nearrow\\)，\\(f[g(x_3)]=f(-1)=1\\)，其中\\(g(x_3)=-1\\)；

在\\([x_3，2]\\)上，\\(f[g(x)]\\searrow\\)，\\(f[g(2)]=f(-2)=-2\\)；

根据上述函数值，做出函数图像，由图像可知方程\\(f[g(x)]=0\\)有且仅有\\(6\\)个根；故①正确；

对于命题②而言，复合函数为\\(g[f(x)]\\)；

在\\([-2，x_4]\\)上，\\(g[f(x)]\\nearrow\\)，\\(g[f(-2)]=g(-2)=-2\\)，\\(g[f(x_4)]=g(-1)=2\\)，其中\\(f(x_4)=-1\\);

在\\([x_4，x_5]\\)上，\\(g[f(x)]\\searrow\\)，\\(g[f(x_5)]=g(0)=1\\)，其中\\(f(x_5)=0\\)；

在\\([x_5，-1]\\)上，\\(g[f(x)]\\searrow\\)，\\(g[f(-1)]=g(1)=-0.3\\)；

在\\([-1，0]\\)上，\\(g[f(x)]\\nearrow\\)，\\(g[f(0)]=g(0)=1\\)；

在\\([0，1]\\)上，\\(g[f(x)]\\nearrow\\)，\\(g[f(1)]=g(-1)=2\\)；

在\\([1，x_6]\\)上，\\(g[f(x)]\\searrow\\)，\\(g[f(x_6)]=g(1)=0\\)，其中\\(f(x_6)=1\\)；

在\\([x_6，2]\\)上，\\(f[g(x)]\\searrow\\)，\\(g[f(2)]=g(2)=-2\\)；

根据上述函数值，做出函数图像，由图像可知方程\\(g[f(x)]=0\\)有且仅有\\(4\\)个根；故②错误；

对于命题③而言，复合函数为\\(f[f(x)]\\)；

在\\([-2，x_4]\\)上，\\(f[f(x)]\\nearrow\\)，\\(f[f(-2)]=f(-2)=-2\\)，\\(f[f(x_4)]=f(-1)=1\\)，其中\\(f(x_4)=-1\\);

在\\([x_4，x_5]\\)上，\\(f[f(x)]\\searrow\\)，\\(f[f(x_5)]=f(0)=0\\)，其中\\(f(x_5)=0\\)；

在\\([x_5，-1]\\)上，\\(f[f(x)]\\searrow\\)，\\(f[f(-1)]=f(1)=-1\\)；

在\\([-1，0]\\)上，\\(f[f(x)]\\nearrow\\)，\\(f[f(0)]=f(0)=0\\)；

在\\([0，1]\\)上，\\(f[f(x)]\\nearrow\\)，\\(f[f(1)]=f(-1)=1\\)；

在\\([1，x_6]\\)上，\\(f[f(x)]\\searrow\\)，\\(f[f(x_6)]=f(1)=-1\\)，其中\\(f(x_6)=1\\)；

在\\([x_6，2]\\)上，\\(f[f(x)]\\nearrow\\)，\\(f[f(2)]=f(2)=2\\)；

根据上述函数值，做出函数图像，由图像可知方程\\(f[f(x)]=0\\)有且仅有\\(5\\)个根；故③正确；

对于命题④而言，复合函数为\\(g[g(x)]\\)；

在\\([-2，x_0]\\)上，\\(g[g(x)]\\nearrow\\)，\\(g[g(-2)]=g(-2)=-2\\)，\\(g[g(x_0)]=g(-1)=2\\)，其中\\(g(x_0)=-1\\);

在\\([x_0，x_1]\\)上，\\(g[g(x)]\\searrow\\)，\\(g[g(x_1)]=f(0)=0\\)，其中\\(g(x_1)=0\\)；

在\\([x_1，x_2]\\)上，\\(g[g(x)]\\searrow\\)，\\(g[g(x_2)]=g(1)=-0.3\\)，其中\\(g(x_2)=1\\)；

在\\([x_2，-1]\\)上，\\(g[g(x)]\\searrow\\)，\\(g[g(-1)]=g(2)=-2\\)；

在\\([-1，0]\\)上，\\(g[g(x)]\\nearrow\\)，\\(g[g(0)]=g(1)=0\\)；

在\\([0，1]\\)上，\\(g[g(x)]\\nearrow\\)，\\(g[g(1)]=g(0)=1\\)；

在\\([1，x_3]\\)上，\\(g[g(x)]\\nearrow\\)，\\(g[g(x_3)]=g(-1)=2\\)，其中\\(g(x_3)=-1\\)；

在\\([x_3，2]\\)上，\\(g[g(x)]\\searrow\\)，\\(g[g(2)]=f(-2)=-2\\)；

根据上述函数值，做出函数图像，由图像可知方程\\(g[g(x)]=0\\)有且仅有\\(4\\)个根；故④正确；

综上所述，正确的命题有①③④。

法2：从外向里分析，由图像可知，\\(-2\\leqslant g(x)\\leqslant 2\\)，\\(-2\\leqslant f(x)\\leqslant 2\\)，

对于命题①而言，由于满足方程\\(f[g(x)]=0\\)的\\(g(x)\\)有\\(3\\)个不同值，由于每个值\\(g(x)\\)又对应了\\(2\\)个\\(x\\)值，故满足\\(f[g(x)]=0\\)的\\(x\\)值有\\(6\\)个，即方程\\(f[g(x)]=0\\)有且仅有\\(6\\)个根，故命题①正确；

[图像使用方法说明]：由\\(y=f(x)\\)的图像可以看出，使得\\(f(x)=0\\)的三个零点值分别为\\(x_1=-1.6\\)，\\(x_2=0\\)，\\(x_3=1.6\\)[估算]，

在函数\\(y=g(x)\\)的图像中，分别做直线\\(g(x)=-1.6\\)，\\(g(x)=0\\)，\\(g(x)=1.6\\)，每一条直线和函数\\(y=g(x)\\)都有\\(2\\)个交点，故共有\\(6\\)个交点。

对于命题②而言，由于满足方程\\(g[f(x)]=0\\)的\\(f(x)\\)有\\(2\\)个不同值，从图中可知，每一个值\\(f(x)\\)，一个\\(f(x)\\)的值在\\((-2，-1)\\)上，另一个\\(f(x)\\)的值在\\((0，1)\\)上，当\\(f(x)\\)的值在\\((-2，-1)\\)上时，原方程有一个解；当\\(f(x)\\)的值在\\((0，1)\\)上时，原方程有\\(3\\)个解，故满足\\(g[f(x)]=0\\)的\\(x\\)值有\\(4\\)个，即方程\\(g[f(x)]=0\\)有且仅有\\(4\\)个根，故命题②不正确；

对于命题③而言，由于满足方程\\(f[f(x)]=0\\)的\\(f(x)\\)有\\(3\\)个不同值，从图中可知，一个\\(f(x)\\)的值在\\((-2，-1)\\)上，一个\\(f(x)\\)的值为\\(0\\)，另一个\\(f(x)\\)的值在\\((1，2)\\)上；当\\(f(x)=0\\)对应了\\(3\\)个不同的\\(x\\)值，当\\(f(x)\\)在\\((-2，-1)\\)上时，只对应一个\\(x\\)值；当\\(f(x)\\)的值在\\((1，2)\\)上时，也只对应一个\\(x\\)的值，故满足\\(f[f(x)]=0\\)的\\(x\\)值有\\(5\\)个，即方程\\(f[f(x)]=0\\)有且仅有\\(5\\)个根，故命题③正确；

对于命题④而言，由于满足方程\\(g[g(x)]=0\\)的\\(g(x)\\)有\\(2\\)个不同值，从图中可知，每个\\(g(x)\\)的值对应\\(2\\)个不同的\\(x\\)值，故满足\\(g[g(x)]=0\\)的\\(x\\)值有\\(4\\)个，即方程\\(g[g(x)]=0\\)有且仅有\\(4\\)个根，故命题④正确；

综上所述，正确的命题有①③④。

• 上次编辑时间：2019-07-21

---

1. 当我们先选择函数\\(g(x)\\)的区间为\\([-2，-1]\\)时，此时虽然能保证内函数\\(g(x)\\)单调递增，但是此时内函数的值域\\(g(x)\\in [-2，2]\\)，其投射到外函数\\(f(x)\\)上时，就放置到了外函数\\(f(x)\\)的定义域\\([-2，2]\\)内，此时外函数的单调性不唯一，说明我们一开始选取的内函数的研究区间\\([-2，-1]\\)有些大了，所以需要压缩；一直压缩到\\([-2，x_0]\\)，其中\\(g(x_0)=-1\\)，这时候内函数的值域\\(g(x)\\in [-2，-1]\\)，刚好投射到外函数的单调递增区间上，说明此时的区间选取是恰当合理的，其他的区间选取与此同理同法；?