计算机组成原理及思维导图

Posted 2022-12-14 qcdxw

第一章、计算机系统概论

---

 1、计算机系统组成及性能：

• 计算机系统是由“硬件”和“软件”组成。

• 衡量一台计算机性能的优劣是根据多项技术指标综合确定的，既包括硬件的各种性能指标，又包括软件的各种功能。

• 计算机系统由硬件和软件两部分组成。

• 计算机系统性能由硬件和软件共同决定。

2、计算机系统5层层次结构：

• 微程序机器、传统机器、操作系统机器、汇编语言机器、高级语言机器

• 微程序机器和传统机器是物理机，其他是虚拟机。

3、冯诺依曼机器的主要特点：

1. 计算机由运算器、存储器、控制器、输入设备和输出设备五大部分组成；

2. 指令和数据存储在存储器中，并可以按地址访问；

3. 指令和数据均以二进制表示；

4. 指令由操作码和地址码构成，操作码指明操作的性质，地址码表示操作数在存储器中的位置；

5. 指令在存储器内按顺序存放，通常按自动的顺序取出执行；

6. 机器以运算器为中心，I/O设备与存储器交换数据也要通过运算器。（后来有以存储器为中心的计算机结构）

4、现代计算机组成图：

 

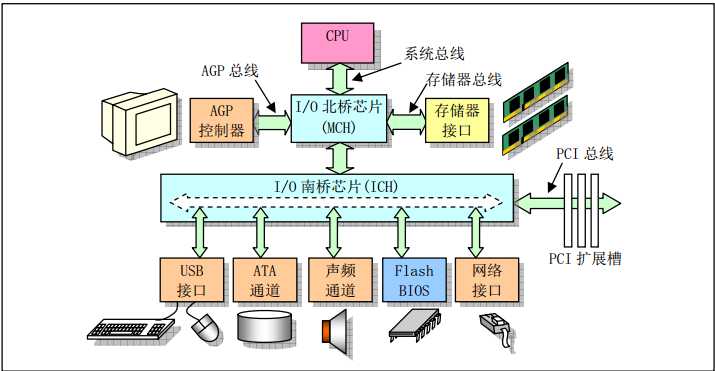
5、计算机储存单元：

• 存储单元：存储一个存储字并具有特定存储地址的存储单位；

• 存储字：一个存储单元中存放的所有的二进制数据，按照某个地址访问某个存储单元获取的二进制数据。

• 存储字长：存储字中二进制数据的位数，即按照某个地址访问某个存储单元获取的二进制数据的位数；

• 存储体：由多个存储单元构成的存储器件。

6、主存储器中的MAR和MDR：

• MAR：存储地址寄存器，保存需要访问的存储单元地址。反映存储单元的个数。

• MDR：存储数据寄存器，缓存读出/写入存储单元的数据。反映存储字长。

• 存储器的最大容量由MAR寄存器的位数和MDR寄存器的位数决定。

7、机器字长和存储字长：

• 机器字长：CPU一次能够处理的二进制数据的位数。

• 存储字长：按照某个地址访问某个存储单元获取的二进制数据的位数。

---

 

第二章、计算机系统

• 硬件

  • 结构
    • 主机
      • CPU
        • ALU运算器
        • CU控制器
      • 存储器
        • 主存
        • 辅存
    • I/O
      • 输入设备
      • 输出设备
  • 主要技术指标
    • 机器字长
      • CPU一次能处理的数据位数
    • 存储容量
      • 存储容量＝存储单元个数×存储字长
    • 运算速度
      • 单位时间执行指令的平均条数，MIPS

• 软件

  • 系统软件

    • 用来管理整个计算机系统
      • 语言处理程序
      • 操作系统
      • 服务性程序
      • 数据库管理系统
      • 网络软件

  • 应用软件

    • 自己下载的普通软件

---

第三章、运算方法和运算部件

1、数据的表示方法和转换

• 机器数正0负1真值:符号位加绝对值

  • 符号数值化的带符号二进制数，称为机器数。

• 余三码:在8421码的基础上，把每个编码都加上0011格雷码:任何两个相邻编码只有1个二进制位不同，而其余3个二进制位相同

  • 当两个余三码想加不产生进位时，应从结果中减去0011;产生进位时，应将进位信号送入高位，本位加0011

• 8421码

  • 权值从高到低为8、4、2、1

    • 算术运算时，需对运算结果进行修正。 方法：如果小于、等于(1001)2，不需要修正；否则加6修正

2、带符号的二进制数据在计算机中的表示方法及运算

（1）原码表示：

• X为正数时，符号位为0；X为负数时，符号位为1。

• 其他位置上与真值一样

• 0存在两种表示形式

　　特点：

• • 值+0，-0的原码分别为00000、10000，形式不唯一；

  • 正数的原码码值随着真值增长而增长，负数的原码码值随着真值增长而减少

• • n+1位原码表示定点整数范围－(2n－1)-----(2n－1)

  • n+1位原码表示定点小数范围 －(1－2－n)------(1－2－n)

　　运算：绝对值相加减，由数值大小决定运算结果符号

（2）反码表示：

• 正数的反码、补码与原码相同

• 负数的反码，按位取反，符号位取反

　　特点：

• • 数值零的反码表示不唯一

  • 正数反码码值随着真值增大而增大，负数反码码值随着真值增大而增大

  • n+1位反码所表示定点整数范围－ (2n－1)-----2n－1，n+1位反码所表示定点小数范围－(1－2－n)-----1－2－n

　　运算：满足[X+Y]反=[X]反+[Y]反，[X－Y]反=[X]反+[－Y]反

 

（3）补码表示：

• 从X求[X]_补：

• X为正数时，[X]_补=X

• X为负数时，①按位求反（符号位不变），②末尾加1

• 从[X]_补求X：

  • [X]_补的符号位为0（正数），[X]_补=X
  • [X]_补的符号位为1（负数），①按位求反（包括符号位），②末尾加1，再在数值前面加上负号-

• 从[X]_补求补：

  • 按位求反（包括符号位）
  • 末尾加1

　　特点：

• • 数值零的补码表示唯一

  • 正数补码码值随着真值增大而增大，负数补码码值随着真值增大而增大

  • n+1位补码所表示定点整数范围－ 2n----2n－1，n+1位补码所表示定点小数范围－1---1－2－n

　　结论：

• 负数的补数＝模＋负数

• 互为补数的绝对值相加＝模

• 在补数中，减法运算即加法运算

　　运算：[X+Y]补=[X]补+[Y]补，[X–Y]补=[X+(–Y)]补=[X]补+[–Y]补

 

（4）移码表示：

• [X]补的符号位取反，即得[X]移

• 为了从码值直接判断对应真值的大小，所以引进移码

　　特点：

• • 最高位是符号位，1表示正，0表示负

  • 数据0有唯一的编码

  • 移码码值随着真值增大而增大

  • n+1位移码所表示定点整数范围－ 2n——2n－1， n+1位移码所表示定点小数范围－1——1－2－n

  • 计算机中，移码常用于表示阶码，故只执行加、减运算

  • 计算机中，移码运算公式需要对结果进行修正

　　运算：

• • 移码定义:[X]移=2的n次方+X

  • 补码定义:[X]补=2的n+1次方+Y

• 阶码求和公式

  • [X]移+[Y]补=[X+Y]移 mod2的n+1次方

  • [X]移+[-Y]补=[X-Y]移

 

（5）补、反、原、移码的相互转换

• 反码----->原码

  • 方法：符号位不变，正数不变，负数数值部分取反。

• 补码----->原码

  • 方法1：正数不变，负数数值部分求反加1。

  • 方法2：串行转换

    • 从最后开始数，遇到第一个“1”，除第一个“1”不变，前面数字分别取反

• 移码----->原码

  • 方法：移码转换为补码，再转换为原码

 

（6）定点数和浮点数

　　定点数：

• • 小数点固定在某个位置上的数据

    • 32位定点小数、定点整数补码的范围

      • 32位定点小数-1～1-2-31

      • 32位定点整数-231～231-1

　　浮点数：

• 根据IEEE754国际标准，常用的浮点数有两种格式

  • • Nmax=Mmax2的Emax

    • Nmin=Mmin2的Emax

• 单精度(32位)=8位阶码+24位尾数

  • 单精度浮点数(32位)，阶码8位(含一位符号位)，尾数24(含一位符号位)，取值范围:-2的127次方～(1-2的-23次方)*2的127次方

• 双精度(64位)=11位阶码+53位尾数

  • 双精度浮点数(64位)，阶码11位(含一位符号位)，尾数53位(含一位符号位)，取值范围:-2的1023次方～(1-2的-52次方)*2的1023次方

• 为了保证数据精度，尾数通常用规格化形式表示:当R=2，且尾数值不为0时，其绝对值应大于或等于(0.5)10小数点位置可以浮动的数据。

  • 左规

  • 右规

• 表示形式：N = M · RE

• 计算机中存储形式

  • Ms+Es+E(n位)+M(m位)

    • 阶码E，一般为整数，用补码或者移码表示；

    • 尾数M，一般为规格化的定点小数，用补码表示；