bzoj4358permuXSY1535seq（莫队+并查集）

Posted 2022-12-13 ez-lcw

考虑莫队，但是我们发现这个东东只支持\(ins\)（至于怎么支持等会再讲），不支持\(del\)操作，所以我们构造一种只\(ins\)不\(del\)的莫队。

由于我们按莫队的方法排序，第一关键字为\(l\)所在的块，第二关键字为\(r\)。所以当排完序后，肯定是当\(l\)所在的块相同时，\(r\)单调递增，所以我们对\(l\)所在的块相同的询问进行处理。设对于块\(B\)，它的末尾位置为\(end\)，我们先找出在排完序中的数组中所有\(l\)所在的块为\(B\)的询问\(q_1\)、\(q_2\)……\(q_k\)，那么这些询问肯定在数组中是连续的，而且它们的\(r\)肯定单调递增。

然后这些询问肯定是长这样的：

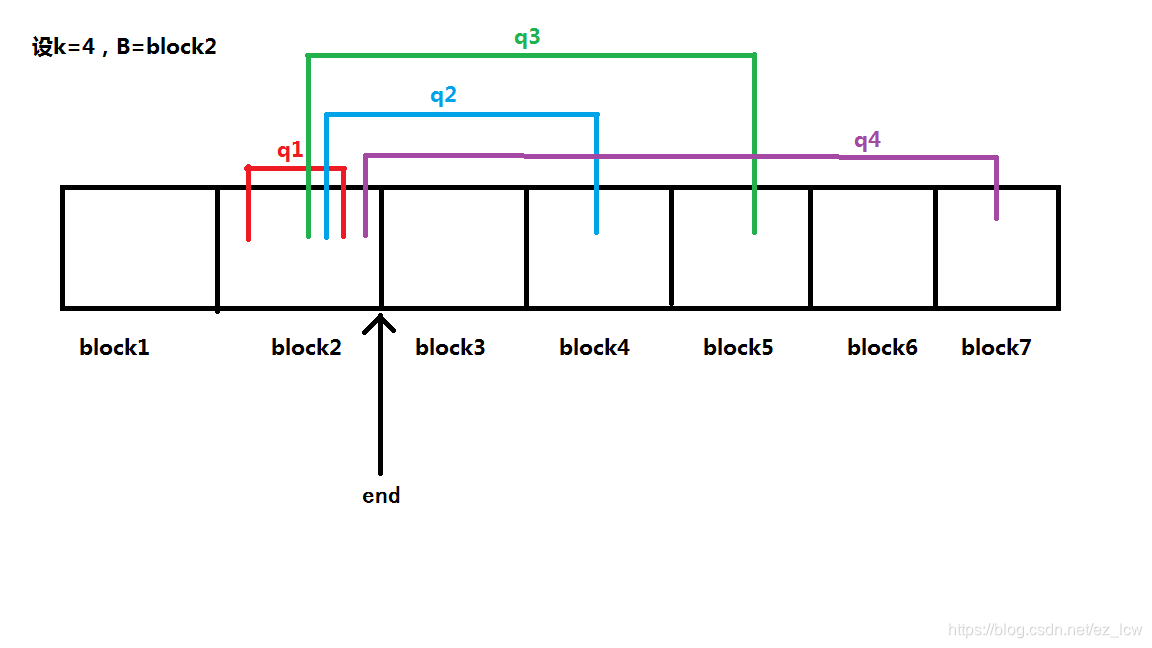
既然\(r\)单调递增，那么对于\(r\)我们直接\(ins\)就好了。而对于\(l\)，由于\(l\)都在块\(B\)里，所以我们每个询问直接从\(end\)暴力向左\(ins\)就可以了。

至于\(ins\)操作，我们考虑用并查集维护。对于插入的每一个值\(x\)，我们在值域中找到它，并把它分别和\(x-1\)和\(x+1\)所在并查集连起来（如果没有就不连），那么答案就是所有并查集中最大的\(size\)。

代码如下：

#include<bits/stdc++.h>

#define N 50010

using namespace std;

struct Question

    int l,r,block,id;
q[N];

int n,m,len,block,a[N],ed[N],ans,Ans[N],st[N],top;
int fa1[N],size[N];
int fa2[N],minn[N],maxn[N];

int find1(int x)

    return fa1[x]==x?x:fa1[x]=find1(fa1[x]);


int find2(int x)

    return fa2[x]==x?x:fa2[x]=find2(fa2[x]);


int get(int x)

    return (x-1)/len+1;


bool operator < (Question a,Question b)

    return a.block==b.block?a.r<b.r:a.l<b.l;


void add1(int u)

    int v;
    fa1[u]=u,size[u]=1;
    if(v=find1(u-1))
        fa1[v]=u,size[u]+=size[v];
    if(v=find1(u+1))
        fa1[v]=u,size[u]+=size[v];
    ans=max(ans,size[u]);


void add2(int u,int &Ans)

    int v;
    st[++top]=u;
    fa2[u]=u,minn[u]=maxn[u]=u;
    if(v=find2(u-1))minn[u]=minn[v];
    else if(v=find1(u-1)) minn[u]-=size[v];
    if(v=find2(u+1))maxn[u]=maxn[v];
    else if(v=find1(u+1)) maxn[u]+=size[v];
    Ans=max(Ans,maxn[u]-minn[u]+1);
    if(minn[u]!=u)fa2[minn[u]]=u,st[++top]=minn[u];
    if(maxn[u]!=u)fa2[maxn[u]]=u,st[++top]=maxn[u];


int main()

    scanf("%d%d",&n,&m);
    block=len=sqrt(n);
    while(block*len<n)block++;
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1,edd=len;i<=block;i++,edd=min(edd+len,n))
        ed[i]=edd;
    for(int i=1;i<=m;i++)
    
        scanf("%d%d",&q[i].l,&q[i].r);
        q[i].block=get(q[i].l),q[i].id=i;
    
    sort(q+1,q+m+1);
    for(int p=1,i=1;i<=m;i=p+1,p=i)
    
        memset(fa1,0,sizeof(fa1));
        ans=0;
        while(q[i].block==q[p+1].block)p++;
        int now=ed[q[i].block];
        for(int j=i;j<=p;j++)
        
            while(now<q[j].r)add1(a[++now]);
            Ans[q[j].id]=ans;
            for(int k=q[j].l;k<=min(q[j].r,ed[q[j].block]);k++)
                add2(a[k],Ans[q[j].id]);
            while(top)
                fa2[st[top--]]=0;
        
    
    for(int i=1;i<=m;i++)
        printf("%d\n",Ans[i]);
    return 0;