每日一题_20191001

Posted 2022-12-08 math521

在等腰\\(\\triangle ABC\\)中,角\\(A,B,C\\)所对的边分别为\\(a,b,c\\),其中\\(B\\)为钝角,且\\(b-\\)\\(\\sqrt3a\\sin A\\)\\(=b\\)\\(\\cos 2A\\),点\\(D\\)与点\\(B\\)在直线\\(AC\\)的两侧,且\\(CD=3AD=3\\),则\\(\\triangle BCD\\)的面积的最大值是\\((\\qquad)\\)
\\(\\mathrmA.\\dfrac34\\sqrt3\\qquad\\) \\(\\mathrmB.4\\sqrt3\\qquad\\) \\(\\mathrmC.\\dfrac54\\sqrt3\\qquad\\) \\(\\mathrmD.3\\)
解析: 由题中所给条件等式可得\\[ \\beginsplit \\sin B-\\sqrt3\\sin^2 A&=\\sin B\\cos 2A \\\\ &=\\sin B-2\\sin B \\sin^2A. \\endsplit\\]所以\\(\\sin B=\\dfrac\\sqrt32\\),又因为\\(B\\)为钝角,所以\\[B=\\dfrac2\\pi3.\\]固定\\(DC\\)边,则\\(A\\)点在以\\(D\\)为圆心,以\\(1\\)为半径的圆上运动,如图所示

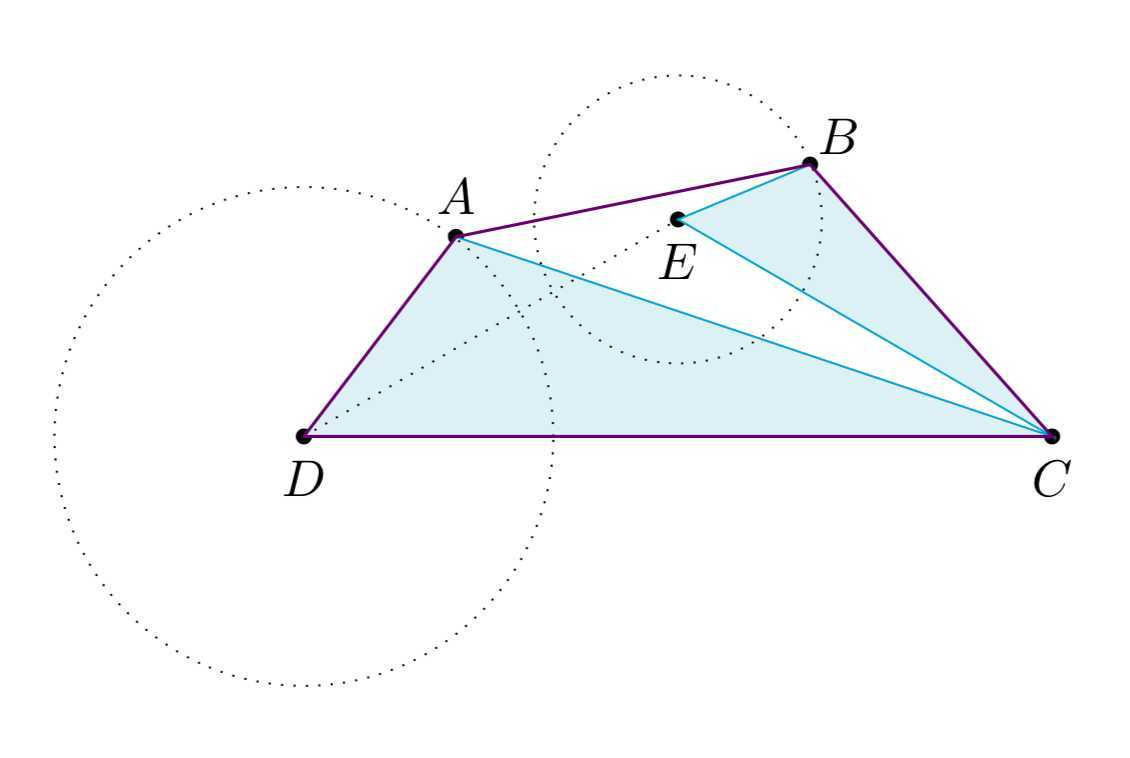
则\\(B\\)点在以\\(E\\)为圆心,以\\(\\dfrac\\sqrt33\\)为半径的圆上运动,其中\\(\\angle DEC=\\dfrac2\\pi3\\),\\(ED=EC\\),于是\\(\\triangle BDC\\)的面积最大值为\\[\\beginsplit S_\\triangle BDC\\big | _\\mathrmmax& =\\dfrac12\\cdot |CD|\\cdot\\left(|EB|+|CE|\\sin\\dfrac\\pi6\\right)\\&=\\dfrac5\\sqrt34. \\endsplit\\]