假币问题

Posted 2022-12-04 edviv

 

Description：

居然有假币！！！ 事情是这样的，现在猪肉涨了，但是农民的工资却不见涨啊，没钱怎么买猪肉啊。老王这就去买猪肉，结果找来的零钱中有假币！！！可惜老王一不小心把它混进了一堆真币里面去了。现在知道假币的重量比真币的质量要轻。给你一个天平，请用最快的时间把那个可恶的假币找出来。

Input：

输入有多行,每一行的值为硬币的数目n,1≤n≤2^30,输入0结束程序

Output：

最少要称多少次一定能把那个假币找出来。输出对应输入行数。

Sample Input Copy：

3

12

0

Sample Output Copy：

1

3

HINT

示例1中共有3枚硬币，所以任意取2个放天平上称量一下。 因为假币的重量比较轻。 如果天平不平衡，则较轻的那枚就是假币。 如果天平平衡，则说明这两枚硬币都是真的，而剩下那枚是假币。

题解：假设我们现在只有三枚硬币，那么我们分成三分A , B, C

1.若 A == B  ，则 C 是假币

2.若 A < B    ,  则 A 是假币

3.若A > B     ,  则 B 是假币

则推出一个结论： f(3) = 1   --- >  继续推广  f( 9 ) = ?

现在分成 3A， 3B， 3C 三部分

1.若 3A == 3B ，则在 3C中查找，现在继续把 3C 分成 3 部分 AA, BB ， CC 三部分

(1).若 AA == BB ，则 CC 是假币 

(2).若 AA <  BB  ,  则 AA  是假币 

(3).若 AA >  BB  ,  则 BB  是假币

2.若 3A >   3B  , 则假币在 3B 中查找， 现在继续把 3B  分成 3 部分 AA， BB ， CC 三部分

(1).若 AA == BB ，则 CC 是假币 

(2).若 AA <  BB  ,  则 AA  是假币 

(3).若 AA >  BB  ,  则 BB  是假币

3.若 3A <   3B , 则假币在 3A 中查找， 现在继续把 3A 分成三部分 AA, BB, CC 三部分

1).若 AA == BB ，则 CC 是假币 

(2).若 AA <  BB  ,  则 AA  是假币 

(3).若 AA >  BB  ,  则 BB  是假币

推出一个结论：f(9) = 2  ----- >  那么我们得出一个结论 f(3^n) = n, f(3^n + 1) = n + 1

最后我们得出一个结论：我们的结论是：有n（n≥3次，就能找出那个假币。）个硬币，其中一个是假币，假币的重量比其他的要重一些。给一架天平，至少称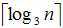次，就能找出那个假币。

分析过程可以画成一棵树，叶子节点顶多只访问一次，然后逐步向下搜索。

“三分”是整个解法的核心。我们选择三分，而不是二分或者四分是有原因的，它的本质是由判定树的特殊结构——三叉树——所决定的。

同时还必须注意一点，我们在三分的时候有两个字很讲究：“均匀”。实际上树的深度 ≥ 中的“=”当且仅当硬币被均匀的分配时才能达到。

这里说的“均匀”是指“在最坏情况下获得最好的效果”。因为一棵树的深度是由它根节点儿子中深度最大的儿子决定的，为了使得整个树深度最小，我们就要务必使得深度最大的儿子深度最小，这就是“均匀”分配的理论根据。

 

 1 #include <iostream>
 2 #include <cmath>
 3 #include <cstdio>
 4 using namespace std;
 5 
 6 int main()
 7 
 8     int n;
 9     while(~scanf("%d",&n))
10     
11         if(n == 0) break;
12         if(n == 1)
13         
14             cout<<"0"<<endl;
15             continue;
16         
17         int count = 0, flag = 0;
18         while(n)
19         
20             if(n%3 && n!= 1)
21                 flag++;
22             n /= 3;
23             count++;
24         
25         if(flag == 0)
26             count--;
27         cout<<count<<endl;
28     
29     return 0;
30