XGBoost的推导和说明

Posted 2022-12-03 dogecheng

一、简介

XGBoost是“Extreme Gradient Boosting”的缩写，其中“Gradient Boosting”一词在论文Greedy Function Approximation: A Gradient Boosting Machine中，由Friedman提出。XGBoost 也是基于这个原始模型改进的。

XGBoost提出后，不仅成为各大数据科学比赛的必杀武器，在实际工作中，XGBoost也在被各大公司广泛地使用。

 

二、树集成

XGBoost属于Boosting集成学习算法的一种，它以CART为基学习器，CART是一棵二叉树，每个叶子都有一个分数，如下图所示

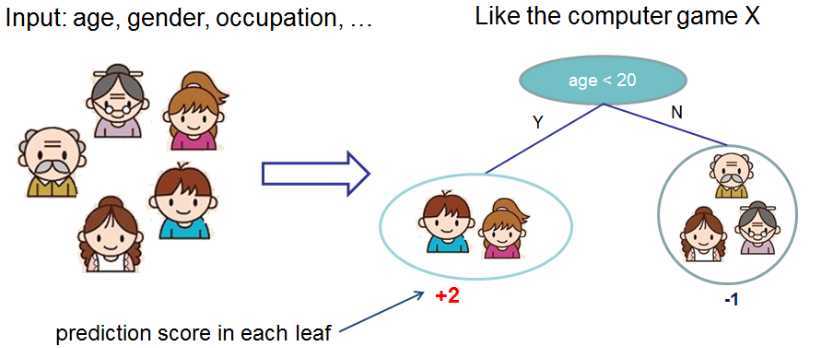
 通常，一棵树过于简单，所以集成学习将多棵树进行结合，常常获得比单棵树优越的泛化性能。

XGBoost是加法模型，它会把多棵树的预测加到一起，预测得分是每棵树的预测分数之和，如下图所示

 

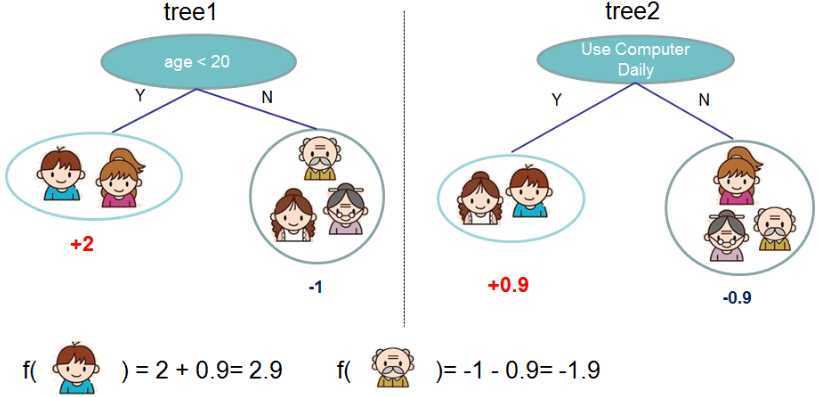
可以用下面的数学公式描述我们的模型

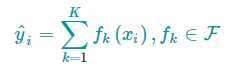
其中，K是树的数量，f是一棵树，F是所有可能的CART树集合。

 

三、树提升

3.1加性训练

XGBoost的目标函数为

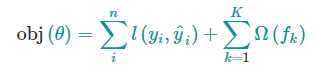
机器学习中的目标函数总是由两个部分组成：训练损失部分 和 正则化部分。

正如上式一样，前面是损失部分，后面是正则化部分，在XGBoost中将全部K棵树的复杂度进行求和，添加到目标函数中作为正则化项。

损失函数用来描述模型与训练数据的契合程度，正则化项用来描述模型的某些性质，比如模型的复杂度。

常见的损失函数有平方损失和log损失，表达式分别如下

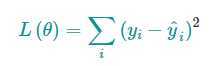
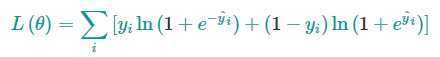
我们要学习的是那些函数f，每个函数都包含了树的结构和叶节点的分数。一次性地学习出所有的树是很棘手的，在XGBoost中采用“加性策略”（additive strategy）学习模型：保持学习到的结果不变，每次添加一棵新的树。 y^t表示第t步的预测值

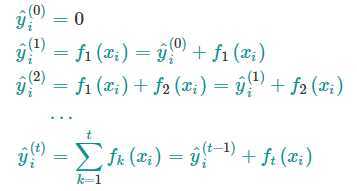
那么我们每次都要留下哪棵树？一个很自然的想法就是选择可以优化我们目标函数的树。前面 t-1 棵树的模型复杂度是一个常数，我的目标函数可以写为

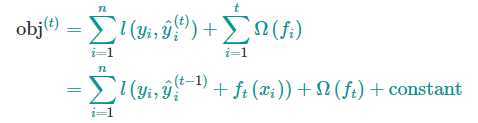
 如果采用平方损失作为损失函数，可以变为下面的形式

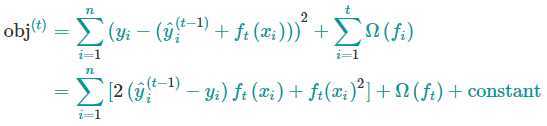
使用平方损失函数有许多友好的地方，它具有一阶项（通常称为残差）和二次项。对于其他形式的损失函数，并不容易获得这么好的形式。一般情况下，我们可以用泰勒公式展开损失函数。

泰勒公式的二阶展开式如下

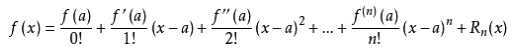展开后的目标函数变为

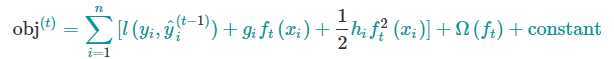
其中，g是一阶偏导，h是二阶偏导

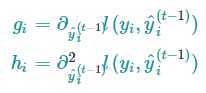
上式中l(y,y^)是前t-1棵树带来的损失，是一个常数，下面把常数项去掉，第t步的目标函数就变成了

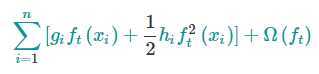这个定义的损失函数只取决于g和h，这就是XGBoost支持自定义损失函数的方式，我们可以优化包括log损失在内的每一个损失函数，对损失函数求一阶和二阶偏导，得到g和h，然后带到上面的公式中就可以了。

 

3.2模型复杂度

我们介绍了模型的训练，但还没定义模型复杂度Ω(f)，我们先改进一棵树的定义为：

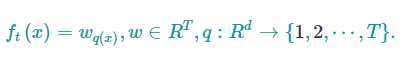其中w是叶节点上的分数向量，q是将输入数据映射到某个叶节点的函数，T是叶节点的数量。我们定义XGBoost的复杂度为

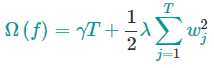它由两部分组成：（1）叶结点的数量 和 （2）叶结点分数向量的L2范数；

 

3.3结构分数

将上面得到式子带到前面得到的目标函数中，有

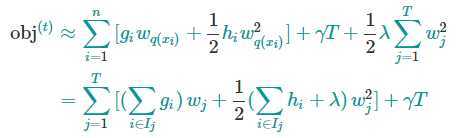其中

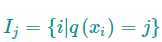
 它存放着被映射到第 j 个叶子节点的数据 ???? 的索引集合。

上面目标函数的第二行中，式子修改了求和符号的下标，由 i=1 变为 i∈Ij，这是因为同一叶节点上的数据有相同的分数。

我们可以进一步压缩这个目标函数：

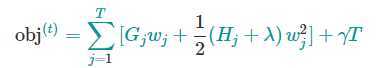
其中

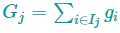
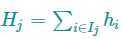
这个目标函数中，wj 彼此独立，而

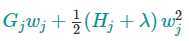
是二次式，我们可以用顶点公式找出最优解

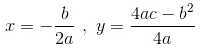
对于给定结构q(x)，使目标函数最小化的w_j的取值和最小化的目标函数为

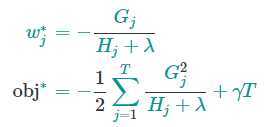
最后一个公式用于衡量树形结构的好坏，分数越小，模型的结构越好。

如果这听起来有点复杂，那么让我们看看下面图片，分数是如何计算的。

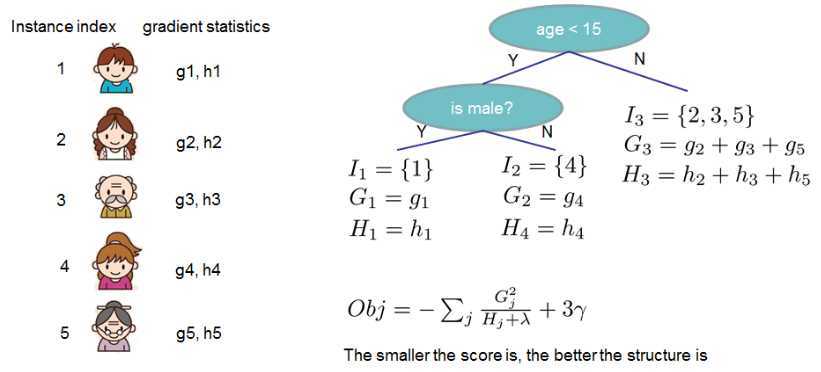
总的来说，对于给定的树结构，我们把 g 和 h 放到它们对应的叶节点中，对这些数据进行求和，然后使用公式计算树有多好。

这个分数类似于决策树中的不纯度，只是它还考虑了模型的复杂性。

 

3.4学习树结构

现在我们有了一种方法来衡量一棵树的质量，理想情况下，我们将枚举所有可能的树并选择最佳的树。

实际上这是棘手的，所以我们将尝试每次优化树的一层。具体来说，我们尝试将一个叶节点分成叶节点，其分数增益为

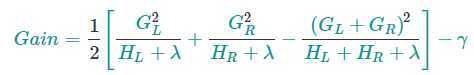
公式从左到右可分解为4个部分

• 1）新左叶上的分数
• 2）新右叶上的分数
• 3）原始叶上的分数
• 4）附加叶上的正则化。

如果增益小于γ，说明添加一个节点没有带来模型性能的提升，容易导致过拟合，我们最好不要添加该分支。这正是基于树的模型中的剪枝技术。

 

对于实值数据，我们通常希望找到最佳分割点。为了有效地做到这一点，我们将所有样本排好序，如下图所示。

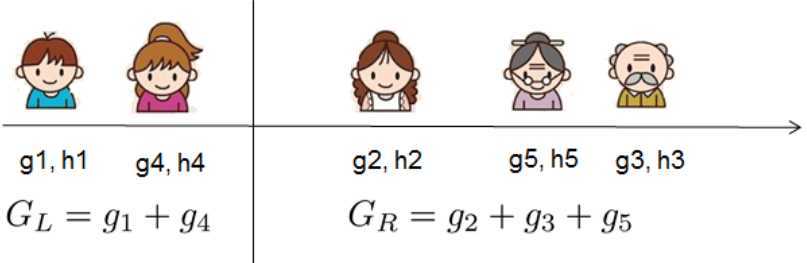然后从左到右的扫描，就足以计算所有可能的分割方案的结构得分，我们可以有效地找到最佳的拆分。

 

 

参考文章

https://xgboost.readthedocs.io/en/latest/tutorials/model.html