A*算法介绍

Posted 2022-11-29 zhonghu

   　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　

　　我们假设要从绿色区域A移动到红色区域B，深蓝色代表不可行走的区域。

　　第一步：首先将寻路区域划分成小格子；

　　第二步：从起点A开始，将其加入到一个由方格组成的openList(开放列表)中。这个openList刚开始只有一个数据，就是起点A。openList里的路径可能是沿途经过的，也有可能不经过。

openList是一个待检查的方格列表。

　　第三步：查看与起点A相邻的方格（忽略其中不可行走的方格），把其中可行走或可到达的方格加入到openList中。把起点A设置为这些相邻方格的父亲。当我们在追踪路径时，这些父节点很重要。

　　第四步：把A节点从openList中移除，加入到closeList（封闭列表）中，closeList的每个方格都是现在不需要再关注的。

　　第五步：我们需要从openList中选一个与A节点相邻的方格。重复下面的步骤，找出具有最小F值的那个节点：

　　F = G + H。G表示从起点A移动到当前节点的移动代价；H表示从指定的节点移动到终点B的估算成本。

如上所述：

　　G是从起点A移动到指定节点的移动代价。在本例中，横向和纵向的移动代价为10，对角线的移动代价为14.之所以使用这些数据，是因为实际的对角移动距离是2的平方根。我们避免了开方

和小数的计算。这并不是代表没有这个能力或不喜欢数学。而是可以使计算变的更快。

　　这里有很多种方法估算H值。这里我们使用Manhattan方法，计算从当前节点横向或纵向移动到达目标所经过的方格数，忽略对角运动，然后把总数乘以10.由于是忽略路径中的障碍物，所以是对剩

余距离的估算值，而不是实际值，因此称为试探法。

 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

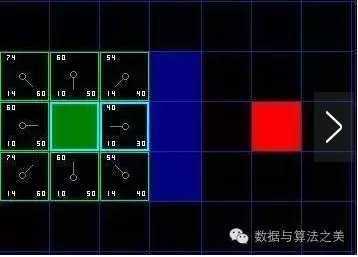
每个方格的左下角表示G；右下角表示H；左上角表示F

 

　　第六步：我们从openList中选择F值最小的节点，然后对其做以下操作：

　　　　1. 把该节点从openList中取出，放到closeList里；

　　　　2. 检查所有与它相邻的方格，忽略其中在closeList中或不可行走的方格；如果可行走的方格不在openList中，则把它们加入到openList中。把当前选定的节点设置为这些新加入的方格的父亲。

　　第七步：如果某个相邻的方格已经在openList中，则检查这条路是否更优。也就是经由当前节点（我们选中的方格）到达那个方格是否具有更小的G值，如果没有则不做任何操作。否则，如果G值更小

则把那个方格的父亲设置为当前方格（重新遍历那个方格的父亲）。然后重新计算那个方格的F值和G值。并且走第八步。

　　第八步：因为再次遍历我们的openList，而左边的那个节点已经在closeList里了，所以只有7个节点了。我们需要选择F值最小的那个。当方格中有相同的F值时，从速度上考虑，选择最后加入openList的方格更快。

我们选择起点A右下方的方格。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　

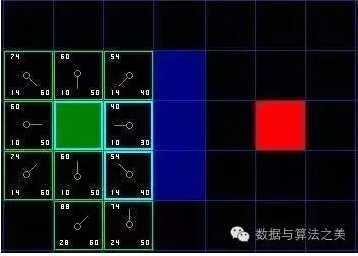
　　第九步：不断重复上个过程，直到把终点也加入到openList中，此时如下图所示：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　

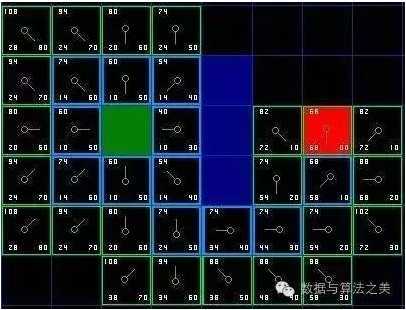
　　　那么我们怎么样去确定实际路径呢？很简单，从终点开始，按着箭头向父节点移动，这样就被带回了起点，也就是路径。