上机实践报告
Posted yi2105
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了上机实践报告相关的知识,希望对你有一定的参考价值。
这里就只记录在上机实践课上面,一时之间没有写出来的 时间复杂度规定为:logn 的题目了
7-3 两个有序序列的中位数
输入格式: 输入分三行。第一行给出序列的公共长度N(0<N≤100000),随后每行输入一个序列的信息,即N个非降序排列的整数。数字用空格间隔。 输出格式: 在一行中输出两个输入序列的并集序列的中位数。 输入样例1: 5 1 3 5 7 9 2 3 4 5 6 输出样例1: 4 输入样例2: 6 -100 -10 1 1 1 1 -50 0 2 3 4 5 输出样例2: 1
由于这个是算法课,遇到题目的时候都需要要求自己时刻往更优的空间和时间复杂度的算法上面去靠拢。
所以我一开始我就想到了如下的想法:

1 #include<iostream> 2 using namespace std; 3 4 int median(int arr1[], int arr2[], int N) 5 6 int i=0, j=0; 7 while((i+j) < N-1) 8 //指针后移 9 if(arr1[i]>arr2[j]) 10 j++; 11 else 12 i++; 13 14 15 //返回 arr1[i]和arr2[j]中的较小值,即为中位数 16 return arr1[i]>arr2[j]?arr2[j]:arr1[i]; 17 18 19 20 int main() 21 22 //输入数组长度N 23 int N; 24 cin>>N; 25 //输入两个数组的元素 26 int arr1[N], arr2[N]; 27 for(int a=0; a<N; a++) 28 cin>>arr1[a]; 29 30 for(int a=0; a<N; a++) 31 cin>>arr2[a]; 32 33 34 //输出中位数 median 35 cout<<median(arr1, arr2, N); 36 37 return 0; 38
1 #include<iostream> 2 using namespace std; 3 4 int median(int arr1[], int arr2[], int N) 5 6 int ans; 7 //两个指针i、j 8 int i=0, j=0; 9 //循环结束条件:指针之和<= N-1 10 while((i+j) <= N-1) 11 if(arr1[i]<arr2[j]) 12 //指针后移 13 i++; 14 ans = arr2[j]; 15 else if(arr1[i]>arr2[j]) 16 j++; 17 ans = arr1[i]; 18 else 19 i++; 20 j++; 21 ans = arr2[j]; 22 23 24 return ans; 25 26 27 28 int main() 29 30 //输入数组长度N 31 int N; 32 cin>>N; 33 int arr1[N], arr2[N]; 34 35 //输入两个数组的元素 36 for(int a=0; a<N; a++) 37 cin>>arr1[a]; 38 39 for(int a=0; a<N; a++) 40 cin>>arr2[a]; 41 42 43 //作初步的判断,两个数组元素是否首位相连 44 //(其实这里的判断应该写到 median函数里面,当时测试点没有过出于方便就直接在外面添加了) 45 if(arr1[N-1]<=arr2[0]) 46 cout<<arr1[N-1]; 47 else if(arr2[N-1]<=arr1[0]) 48 cout<<arr2[N-1]; 49 else 50 //输出 median函数结果 51 cout<<median(arr1, arr2, N); 52 53 54 //return0,函数结束 55 return 0; 56
以下是图解:
①初始状态:
N -1 = 4
i+j = 0 < 4
由于1<2,作为指针功能的 i 往后移
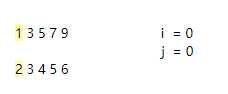
②
i+j = 1 < 4 循环继续
由于2<3,作为指针功能的 j 往后移
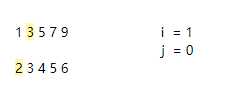
③
i+j = 2 < 4 循环继续
由于3=3,作为指针功能的 i 往后移

④
i+j = 3 < 4 循环继续
由于3<5,作为指针功能的 j 往后移

⑤
i+j = 4 = 4 循环结束
由于4<5,返回较小值4,即为中位数
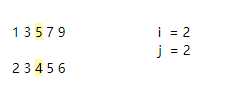
这样确实比更一般的想法:将两个数组合成一个数组后,排序再求中位数来得简单许多。
但是这个方法依旧停留在O(n)的时间复杂度上面,远大于老师所要求的 O(logn) 的时间复杂度。
当我打算摔破瓦罐一切重来的时候,发现(其实早就发现了)只要有 logn 出现的地方,一般都离不开分治法的思想,也就是递归。
于是又做了下一步尝试:

1 #include <iostream> 2 using namespace std; 3 4 /**参数: 5 *数组1,数组1的左边起始下标,数组1的右边结束下标; 6 *数组2,数组2的左边起始下标,数组2的右边结束下标。 7 **/ 8 int median(int a[],int a_l,int a_r,int b[],int b_l,int b_r) 9 int a_m, b_m; 10 int ans; 11 12 //当数组1没有元素时,返回a[a_r]和 b[b_l]中的较小值 (为中位数) 13 if(a_l == a_r) 14 return a[a_r] < b[b_l] ? a[a_r] : b[b_l]; 15 16 17 //得到数组1、数组2的中间下标值 18 a_m = (a_l + a_r) / 2; 19 b_m = (b_l + b_r) / 2; 20 21 //当数组1、数组2中间值相等时,该值即为中位数 22 if(a[a_m] == b[b_m]) 23 ans = a[a_m]; 24 else if(a[a_m] < b[b_m]) 25 //奇数情况,同时避免了只剩余两个数会陷入死循环的状态 26 if((a_r - a_l + 1) % 2 ==0) 27 a_m += 1; 28 29 30 //递归调用 median函数 31 ans = median(a,a_m,a_r,b,b_l,b_m); 32 else 33 if((a_r - a_l + 1) % 2 ==0) 34 b_m += 1; 35 36 ans = median(a,a_l,a_m,b,b_m,b_r); 37 38 39 //返回中位数 40 return ans; 41 42 43 int main() 44 //输入数组的长度n 45 int n; 46 cin >> n; 47 48 //输入数组的元素 49 int arr1[n],arr2[n]; 50 for(int i = 0;i<n;i++) 51 cin >> arr1[i]; 52 53 for(int j = 0;j<n;j++) 54 cin >> arr2[j]; 55 56 //输出中位数结果 57 cout << median(arr1,0,n-1,arr2,0,n-1); 58 59 return 0; 60
这次确实是O(logn)的时间复杂度了。
以下为图解:
①初始状态:
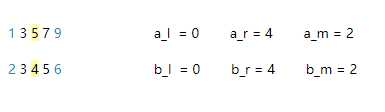
②
总结:
最近这一个月都挺忙的...
很多超纲的知识需要自己去学,反观上课才是比较轻松的活了...
不过在算法课上面也是绞尽脑汁去汲取新的知识,也是一种记录了。
以上是关于上机实践报告的主要内容,如果未能解决你的问题,请参考以下文章
