数据结构mooc陈越第一周总结

Posted 2022-11-24 394991776zyh

1.2

空间复杂度S(n) ——根据算法写成的程序在执行时 占用存储单元的长度。这个长度往往与输入数据的 规模有关。空间复杂度过高的算法可能导致使用的 内存超限，造成程序非正常中断。

时间复杂度T(n) ——根据算法写成的程序在执行时 耗费时间的长度。这个长度往往也与输入数据的规 模有关。时间复杂度过高的低效算法可能导致我们 在有生之年都等不到运行结果。

在分析一般算法的效率时，我们经常关注下面 两种复杂度
最坏情况复杂度 Tworst( n ) 
平均复杂度 Tavg( n )

T(n) = O(f(n)) 表示存在常数C >0, n0>0 使得当 n>=n0 时有T(n) <= C·f(n)
T(n) = ?(g(n)) 表示存在常数C >0, n0>0 使得当 n>=n0 时有T(n) >= C·g(n)
T(n) = Θ(h(n)) 表示同时有T(n) = O(h(n)) 和 T(n) = ?(h(n))

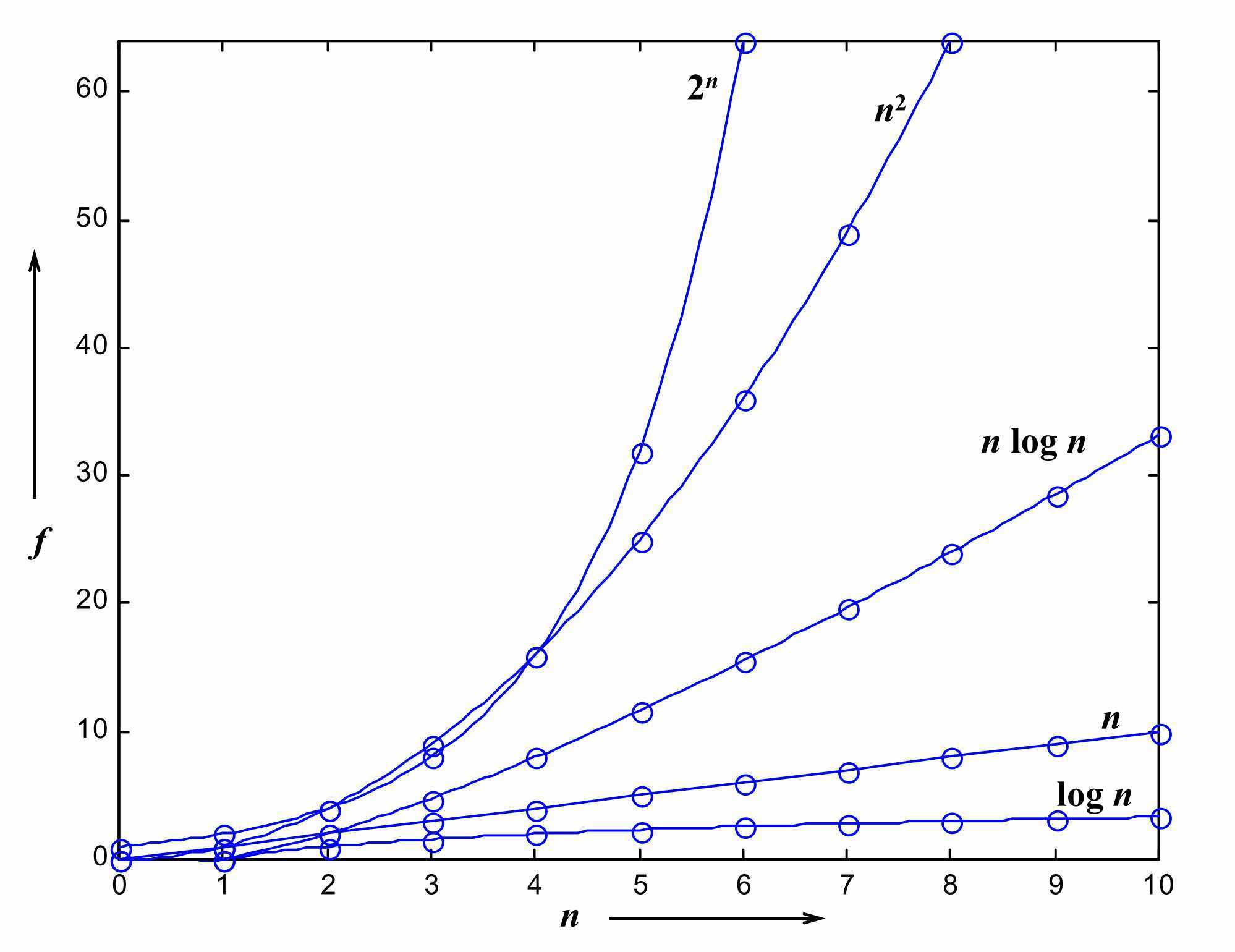
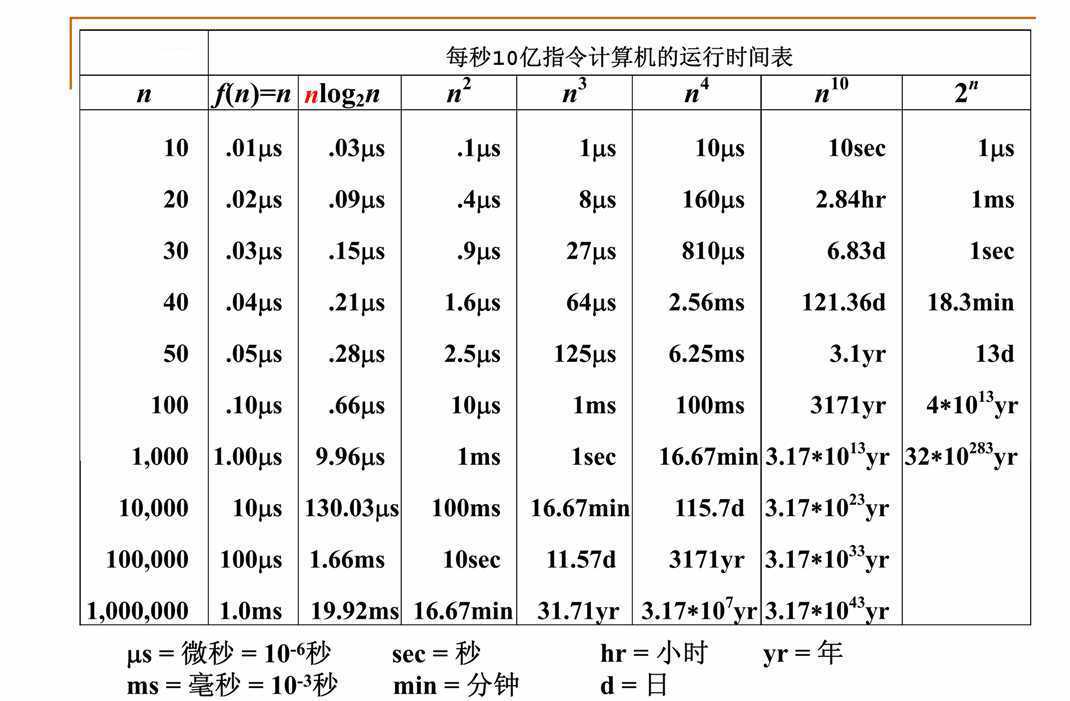
 若两段算法分别有复杂度T1(n) = O(f1(n)) 和T2(n) = O(f2(n))，则 
T1(n) + T2(n) = max( O(f1(n)), O(f2(n)) ) 

T1(n) x T2(n) = O( f1(n) x f2(n) )
 若T(n)是关于n的k阶多项式，那么T(n)=Θ(n^k) 

一个for循环的时间复杂度等于循环次数乘以循环体 代码的复杂度
 if-else 结构的复杂度取决于if的条件判断复杂度 和两个分枝部分的复杂度，总体复杂度取三者中最大

算法1

int MaxSubseqSum1(int A[],int N)  
  
    int ThisSum,MaxSum = 0;  
    int i,j,l;  
    for(i = 0;i < N;i++)   //i是子列左端位置   
      
        for(j = i;j < N;j++) //j是子列右端位置   
          
            ThisSum = 0;     //ThisSum是从A[i]到A[j]的子列和  
            for(k = i;k < j;k++)  
                 ThisSum += A[k];  
            if(ThisSum > MaxSum)  //如果刚得到的这个子列和更大   
                MaxSum = ThisSum;   //则更新结果   
        //j循环结束   
          
    //i循环结束  
    return MaxSum;   
  

算法2

int MaxSubseqSum2(int A[],int N)  
  
    int ThisSum,MaxSum = 0;  
    int i,j;  
    for(i = 0;i < N;i++) //i是子列左端位置   
      
        ThisSum = 0;    //ThisSum是从A[i]到A[j]的子列和   
        for(j = i;j < N;j++) //j是子列右端位置   
          
            ThisSum += A[j];    //对于相同的i不同的j，只要在j-1次循环的基础上累加1项即可  
            if(ThisSum > MaxSum) //如果刚得到的这个子列和更大   
                MaxSum = ThisSum;   //则更新结果   
           //j循环结束   
       //i循环结束   
    return MaxSum;
  

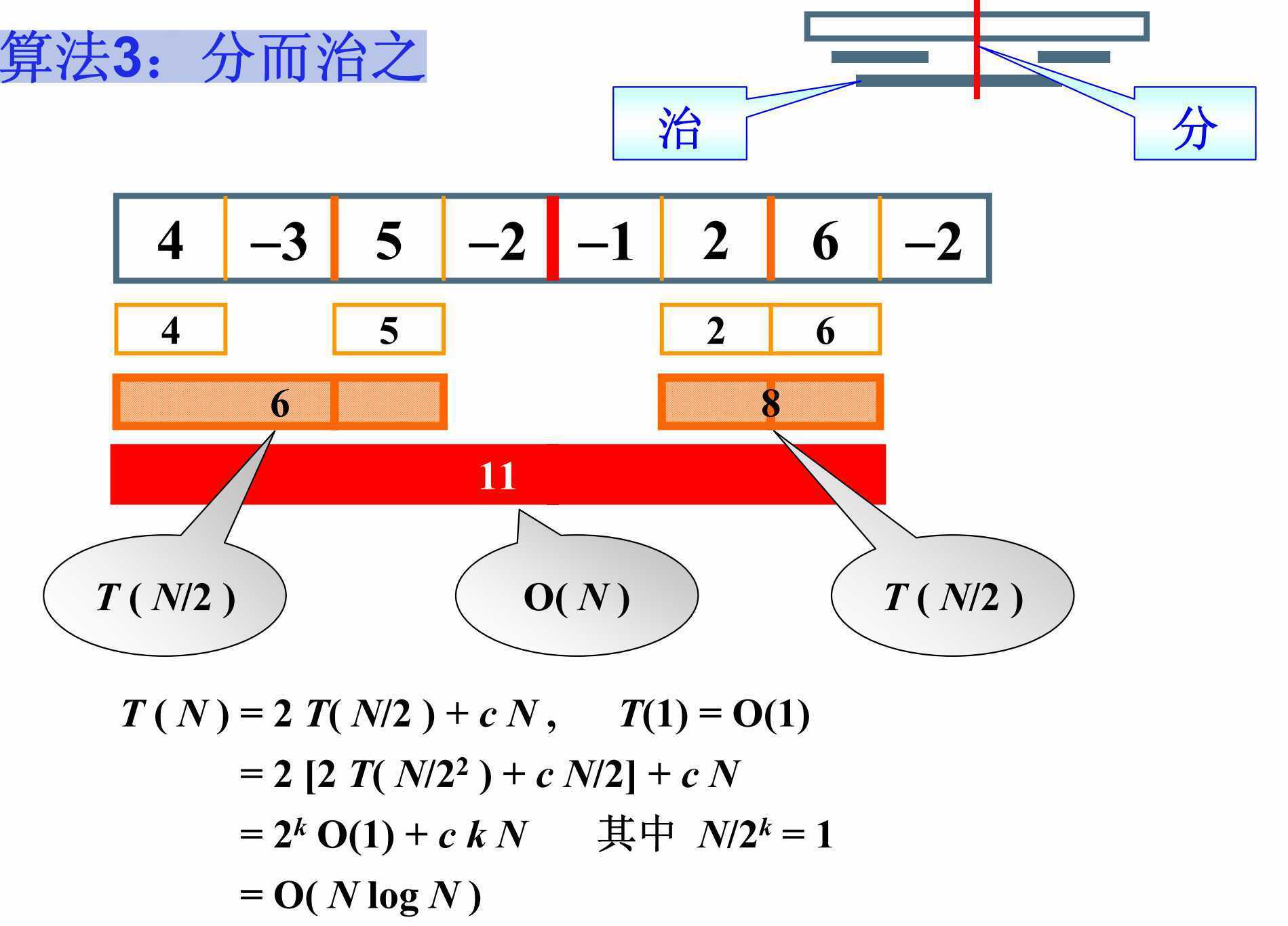
算法3：分而治之

分而治之的思想：把复杂的问题切分成小的块，分头去解决它们，最后将结果合并。

应用在最大子列和问题上，即将存储数据的数组看成左右两部分，分别求出两部分的最大子列和以及贯穿中间线的最大子列和，三个部分中的最大部分即我们要求的最大子列和。

int Max3( int A, int B, int C )  
 /* 返回3个整数中的最大值 */  
    return A > B ? A > C ? A : C : B > C ? B : C;  
  
   
int DivideAndConquer( int List[], int left, int right )  
 /* 分治法求List[left]到List[right]的最大子列和 */  
    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */  
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/  
   
    int LeftBorderSum, RightBorderSum;  
    int center, i;  
   
    if( left == right )  /* 递归的终止条件，子列只有1个数字 */  
        if( List[left] > 0 )  return List[left];  
    else return 0;  
   
    /* 下面是"分"的过程 */  
    center = ( left + right ) / 2; /* 找到中分点 */  
    /* 递归求得两边子列的最大和 */  
    MaxLeftSum = DivideAndConquer( List, left, center );  
    MaxRightSum = DivideAndConquer( List, center+1, right );  
   
    /* 下面求跨分界线的最大子列和 */  
    MaxLeftBorderSum = 0; LeftBorderSum = 0;  
    for( i=center; i>=left; i-- )  /* 从中线向左扫描 */  
        LeftBorderSum += List[i];  
        if( LeftBorderSum > MaxLeftBorderSum )  
            MaxLeftBorderSum = LeftBorderSum;  
     /* 左边扫描结束 */  
   
    MaxRightBorderSum = 0; RightBorderSum = 0;  
    for( i=center+1; i<=right; i++ )  /* 从中线向右扫描 */  
        RightBorderSum += List[i];  
        if( RightBorderSum > MaxRightBorderSum )  
            MaxRightBorderSum = RightBorderSum;  
     /* 右边扫描结束 */  
   
    /* 下面返回"治"的结果 */  
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );  
  
   
int MaxSubseqSum3( int List[], int N )  
 /* 保持与前2种算法相同的函数接口 */  
    return DivideAndConquer( List, 0, N-1 );  
  

算法4

int MaxSubseqSum4(int A[],int N)

int ThisSum,MaxSum;
int i;
ThisSum = MaxSum = 0;
for(i = 0;i < N;i++)

ThisSum += A[i];    //向右累加
if(ThisSum > MaxSum)
MaxSum = ThisSum;    //发现更大和则更新当前结果
else if(ThisSum < 0)    //如果当前子列和为负
ThisSum = 0;//则不可能使后面的部分和增大，抛弃之

return MaxSum;

课后习题

1.本题要求实现二分查找算法。

函数接口定义：

Position BinarySearch( List L, ElementType X );

其中List结构定义如下：

typedef int Position;
typedef struct LNode *List;
struct LNode 
    ElementType Data[MAXSIZE];
    Position Last; /* 保存线性表中最后一个元素的位置 */
;

L是用户传入的一个线性表，其中ElementType元素可以通过>、=、<进行比较，并且题目保证传入的数据是递增有序的。函数BinarySearch要查找X在Data中的位置，即数组下标（注意：元素从下标1开始存储）。找到则返回下标，否则返回一个特殊的失败标记NotFound。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 10
#define NotFound 0
typedef int ElementType;

typedef int Position;
typedef struct LNode *List;
struct LNode 
    ElementType Data[MAXSIZE];
    Position Last; /* 保存线性表中最后一个元素的位置 */
;

List ReadInput(); /* 裁判实现，细节不表。元素从下标1开始存储 */
Position BinarySearch( List L, ElementType X );

int main()

    List L;
    ElementType X;
    Position P;

    L = ReadInput();
    scanf("%d", &X);
    P = BinarySearch( L, X );
    printf("%d\\n", P);

    return 0;


/* 你的代码将被嵌在这里 */

输入样例1：

5
12 31 55 89 101
31

输出样例1：

2

输入样例2：

3
26 78 233
31

输出样例2：

0
我的答案：

Position BinarySearch(List L , ElementType X)

    if (L == NULL)
        return NotFound;
    int low = 1, high = L->Last, mid;
    //low一定小于等于high 如下标为1、2、3 要查询的是下标为1的数,第一次是比较下标为2的,不符合 high就变成了1,如果写low<high就会返回错误的结果
    while (low <= high)
        mid = (low + high) / 2;
        if (L->Data[mid] == X)return mid;
        else if (L->Data[mid] > X)high = mid - 1;
        else low = mid + 1;
    
    return NotFound;

 

给定K个整数组成的序列 N?1??, N?2??, ..., N?K?? ，“连续子列”被定义为 N?i??, N?i+1??, ..., N?j?? ，其中 1。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列 -2, 11, -4, 13, -5, -2 ，其连续子列 11, -4, 13 有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

• 数据1：与样例等价，测试基本正确性；
• 数据2：102个随机整数；
• 数据3：103个随机整数；
• 数据4：104个随机整数；
• 数据5：105个随机整数；

输入格式:

输入第1行给出正整数K (≤)；第2行给出K个整数，其间以空格分隔。

输出格式:

在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

输入样例:

6
-2 11 -4 13 -5 -2

输出样例:

20
我的答案

#include<stdio.h>
int main()
    int result=0,thissum=0,N,digit;
    scanf("%d",&N);
    for(int i=0;i<N;i++)
        scanf("%d",&digit);
        thissum+=digit;
        if(thissum>result)
            result=thissum;
        if(thissum<0)   thissum=0;
    
    printf("%d",result);
    return 0;

Given a sequence of K integers  N?1??, N?2??, ..., N?K?? . A continuous subsequence is defined to be  N?i??, N?i+1??, ..., N?j??  where 1. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence -2, 11, -4, 13, -5, -2 , its maximum subsequence is 11, -4, 13 with the largest sum being 20.

Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.

Input Specification:

Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (≤). The second line contains K numbers, separated by a space.

Output Specification:

For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.

Sample Input:

10
-10 1 2 3 4 -5 -23 3 7 -21

Sample Output:

10 1 4
我的答案

#include <stdio.h>

int main()

    int n, flag = 1, first_flag = 1, positive_flag = 0;
    int sum = 0, summax = 0;
    int st = 0, end = 0, st_max = 0, end_max = 0, first = 0;
    scanf("%d", &n);

    for (int i = 0; i < n; i++) 
        scanf("%d", &end);

        first_flag && (first = end) && (first_flag = 0); // 短路求值
        end >= 0 && (positive_flag = 1);                 // 短路求值
        !flag || (flag = 0) || (st = end);               // 短路求值

        sum += end;
        if (summax < sum) 
            summax = sum;
            st_max = st;
            end_max = end;
        
        !(sum < 0) || !(flag = 1) || (sum = 0);          // 短路求值
    

    if (positive_flag)
        printf("%d %d %d", summax, st_max, end_max);
    else
        printf("%d %d %d", summax, first, end);
    return 0;