机器学习之HMM

Posted 2022-11-17 jacker2019

必要的数学知识

1.联合概率与边缘概率

联合概率是指多维随机变量中同时满足多个变量时候的概率，也就是共同发生的概率。A,B的联合概率通常写成 P(A∩B)或 P(AB)或  P(AB)。

　　对于离散的变量，联合概率可以用表格形式表示或者求和表示，连续的变量可以使用积分表示（若是二维就一个二重积分）

边缘概率是指多维随机变量中只满足部分变量时的概率

图片帮助理解：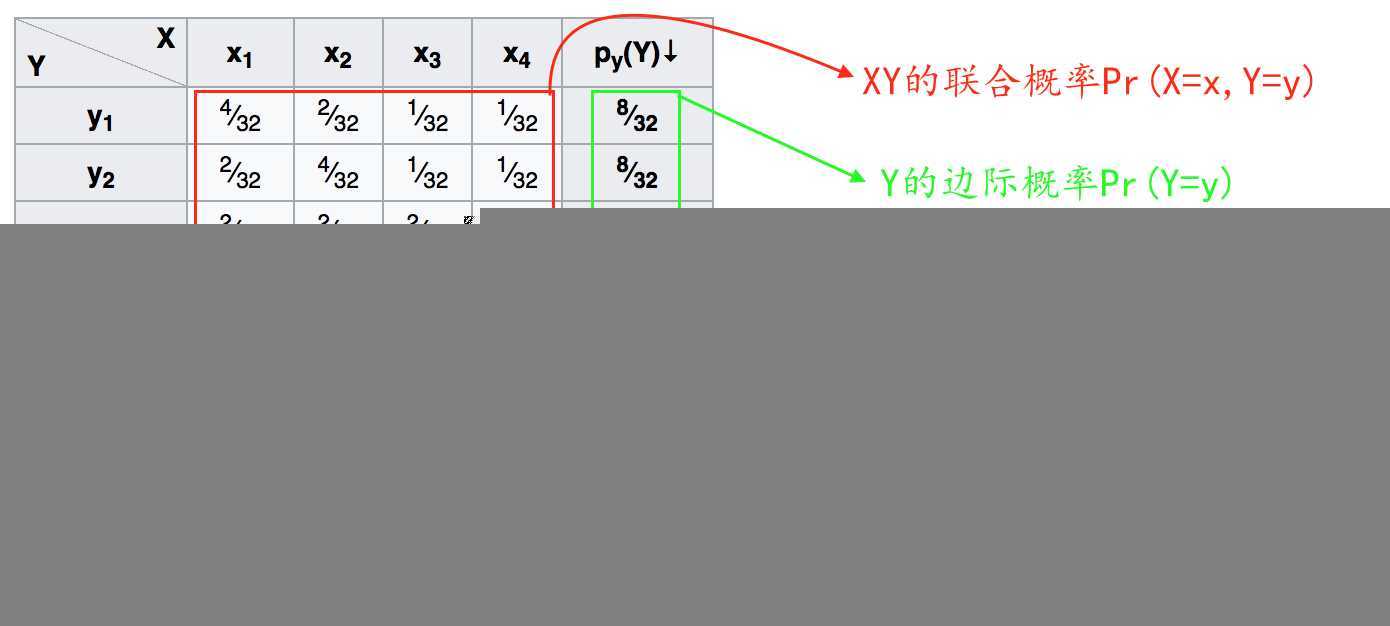

 联合概率与边缘概率的关系

X的边缘概率等于联合概率 所以j的联合概率相加

 边缘概率分布公式：

 联合概率的条件概率链式法则：

举例：P(a,b,c)=P(a|b,c)*P(b,c)

　　　　　　=P(a|b,c)*P(b|c)*P(c)

条件概率：

独立性（XY相互独立）

P（X,Y）=P(X) *P(Y)

条件独立性

P（X,Y|Z）=P(X|Z)*P(Y|Z)

2.EM算法

 

         

关于EM算法利用jensen不等式近似实现极大似然估计的推导过程：https://zhuanlan.zhihu.com/p/36331115

 

 

隐马尔可夫模型（HMM）

1.基本模型样式

 

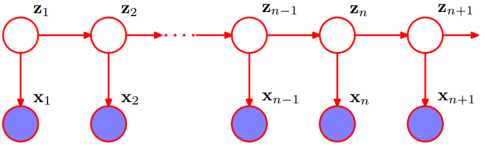
 上图中，白圈代表状态变量，蓝圈代表观测变量。所以白圈那一行是状态序列（隐状态），而白圈这一行是观测序列。

 

2.模型的数学表达

HMM由隐含状态S、可观测状态O、初始状态概率矩阵pi、隐含状态概率转移矩阵A、可观测值转移矩阵B（混淆矩阵）组成，可以使用一个三元组进行表述：

 

 

3.Markov两个假设

3.1齐次假设：表示 t 时刻的状态只与 t-1 时刻的状态有关

3.2观测独立性假设：表示 t 时刻的观测变量只与 t 时刻的状态有关

 

 

4.解决三个问题

概率计算问题(Evalution )：前向后向算法，已知模型 λ = (A, B, π)和观测序列O=o1, o2, o3 ...，计算模型λ下观测O出现的概率P(O | λ)

学习问题（learning）：EM算法，已知观测序列O=o1, o2, o3 ...，计算估计模型λ = (A, B, π)的参数即推断状态的转移情况，使得在该参数下该模型的观测序列P(O | λ)最大

预测问题（Decoding）：Viterbi算法，已知模型λ = (A, B, π)和观测序列O=o1, o2, o3 ...，求给定观测序列条件概率P(I | O，λ)最大的状态序列 I

 

4.1HMM模型的实质

HMM实际上就是建立建模 P(O,Q),对于给定的lamda 进行建模：

 

   

 

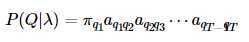
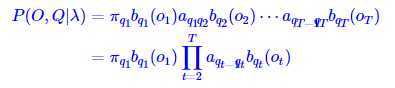
5.关于转移矩阵AB及Pai的定义

5.1状态转移矩阵A：根据Markov齐次假设去定义

状态转移矩阵是一个NxN的矩阵，表示一个状态有N种可能性，前一个状态也有N种可能性。a_ij表示状态从前一个的 i 状态转变为现在的 j 状态的概率。

 

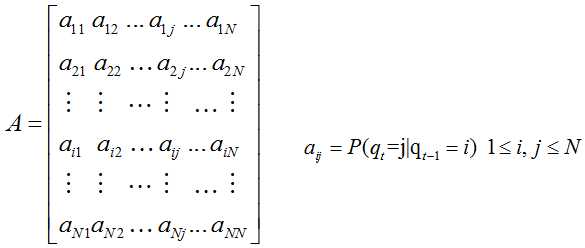
 上述式中 q 表示状态，所以 q_t 表示 t 时刻的转态。

5.2观测概率矩阵B（混淆矩阵）：根据Markov 观测独立性假设定义

观测概率矩阵B是一个NxM的矩阵，表示对于N种状态，在这N种状态下对应的M个可观测变量的概率（比如说在晴天状态下，观测到的湿度、温度、风速等观测量的概率）。

b_j(k)表示 j 状态下的第 k 个观测量的 概率。 

 

 上式中P（o_t=v_k|i_t=q_j）表示t 时刻状态为 q_j 的情况下，t 时刻观察量为 v_k的概率。

 5.3隐藏状态概率分布 pai（t=1时刻的状态）

 举例总结：

针对上述将的几个转移矩阵概念和初始状态pai，举出一个盒子中摸球的例子帮助理解。

 

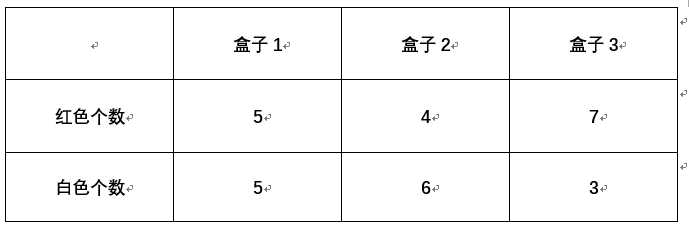
 摸球规则：

　　开始的时候，从第一个盒子抽球的概率是0.2，从第二个盒子抽球的概率是0.4，从第三个盒子抽球的概率是0.4。以这个概率抽一次球后，将球放回。然后从当前盒子转移到下一个盒子进行抽球。规则是：如果当前抽球的盒子是第一个盒子，则以0.5的概率仍然留在第一个盒子继续抽球，以0.2的概率去第二个盒子抽球，以0.3的概率去第三个盒子抽球。如果当前抽球的盒子是第二个盒子，则以0.5的概率仍然留在第二个盒子继续抽球，以0.3的概率去第一个盒子抽球，以0.2的概率去第三个盒子抽球。如果当前抽球的盒子是第三个盒子，则以0.5的概率仍然留在第三个盒子继续抽球，以0.2的概率去第一个盒子抽球，以0.3的概率去第二个盒子抽球。

 　　从紫色背景的摸球规则中，可以推断出初始矩阵：

 

 　　从绿色背景的摸球规则中，可以推断出状态转移矩阵为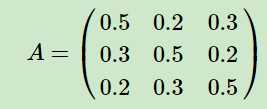(矩阵的行列表示盒子123，数据表示转移概率)

 

 　　从数据表格中可以推断出观测概率矩阵为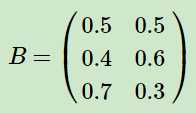：（矩阵的2列标识对应的观测结果，3行表示该观测结果下来自于不同盒子的概率）

 

 【注】集合与序列的问题，集合不重复，所以这个案例中，观测集合为 红，白，状态集合为盒子1，盒子2，盒子3。所以M=2,N=3.但是观测序列可以是[红，白，红]等非2个元素的组成

 

概率计算问题

在给定模型 λ和 观测序列 O的情况下计算 P（O|λ）

思路：

1. 列举所有可能的长度为T的状态序列I = i₁, i₂, ..., i_T；每个i都有N个可能的取值。
2. 求各个状态序列I与观测序列 的联合概率P(O,I|λ)；
3. 所有可能的状态序列求和∑_I P(O,I|λ)得到P(O|λ)。

用到的公式：边缘概率公式 和条件概率的链式法则

　　∵ P（O|λ）=Σ_IP(O,I|λ)    ←边缘概率公式

　　P(O,I|λ)= P(O|I, λ)P(I|λ)   ←链式法则

第一步：

　　P(I|λ)= P(i₁,i₂, ..., i_T |λ)  

　　　　= P(i₁ |λ)P(i₂ | i_1, λ)P(i₃ | i_2, λ)...P(i_T | i_T-1, λ)  ←链式法则

　　上面的P(i₁ |λ) 是初始为状态i₁的概率，P(i₂ | i_1, λ) 是从状态 i₁转移到 i₂的概率，其他同理，于是分别使用初始概率分布π 和状态转移矩阵A，就得到结果：

　　∴

第二步：

　　P(O|I, λ) 在序列 I的条件下观测，所以

 　　于是带入求和可得：

　  　

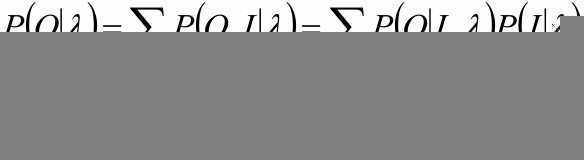
复杂度为：a_ij 的复杂度为N^T，b的复杂度为 T，所以总的复杂度 O(Tn^T)

 

前向算法（Forwarding）/后向算法

前后向算法的区别之处：

　　

 

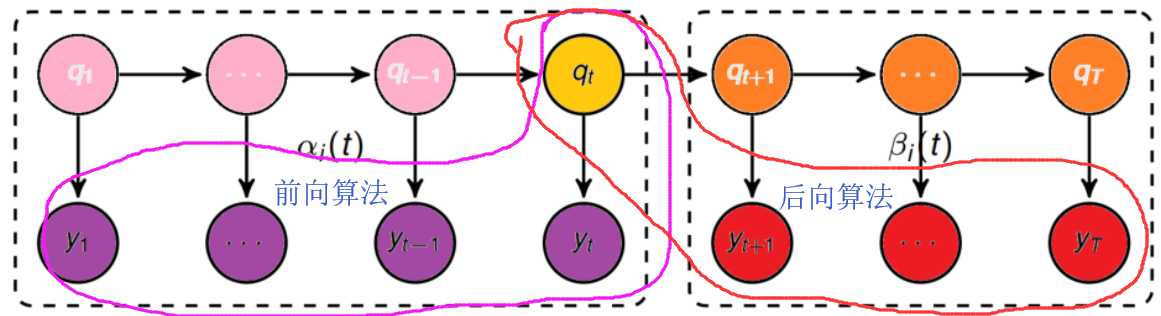
 在概念的定义上：

　　前向算法：当第t个时刻的状态为i时，前面的时刻分别观测到y₁,y₂, ..., y_t的概率，即：

 

 　  后向算法：当第t个时刻的状态为i时，后面的时刻分别观测到y_t+1,y_t+2, ..., y_T的概率，即：

前向算法推导过程：在给定模型 λ和 观测序列 O的情况下计算 P（O|λ）

 　　在上面的粗暴概率计算中，复杂度大，所以我们可以使用递推公式来降低复杂度，于是在这里就是构造一个递推。

 

 又因α_t(i)=P（o₁,o₂,o₃...o_t,i_t=q_i|λ）,P(i_t+1=q_j|i_t=q_i)=a_ij,然后初P(o_t+1|i_t+1=q_j)=b_j(o_t+1)

所以整个递推公式为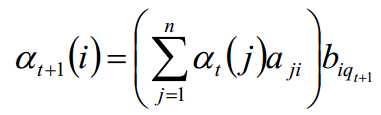

 

 后向算法类似于前向算法：

 

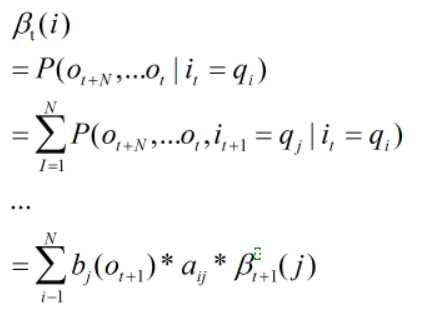
 Baum Welch-EM算法

 已知观测序列O=o1, o2, o3 ...，计算估计模型λ = (A, B, π)的参数即推断状态的转移情况，使得在该参数下该模型的观测序列P(O | λ)最大

而我们知道，观测O由对应的状态决定，所以这里还隐含了状态这个未知变量，所以这个求解问题实际是一个隐变量求解问题，于是需要使用EM算法解决

 1.求Q函数

 

 因为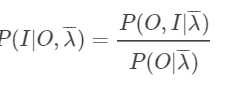，其中 O与 λ 已知，所以P(O| λ) 可以看成一个常数。

 

于是

 

 2.求解Q函数

因为完全数据对数似然：

 

 所以 Q函数可以写成

 

 

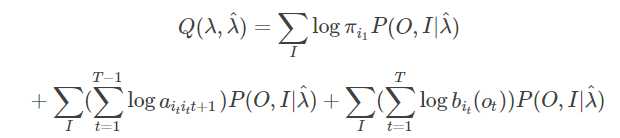
 求解最大化的过程参考此贴：https://blog.csdn.net/u014688145/article/details/53046765

 

 

Viterbi（维特比）算法

 已知模型与观测序列，求取最大的 状态序列。也就是求取 ，但是由于，并且这边观测O与模型λ处于已知状态，所以可以认为是一个常数，于是这个问题就等价于求取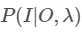，所以引入δ变量的时候按照这个求取就行了。

 

维特比算法的流程：

 

 

 

 对于这个流程的理解可以看https://zhuanlan.zhihu.com/p/41864904上面的例子，实际在维特比算法的计算过程中存在两个T分别保存最大概率和最大概率的那个来自那个状态。

还有https://zhuanlan.zhihu.com/p/63087935帮助理解（感觉这个更直观）

 

 

 

 

 

 

 参考：

https://www.cnblogs.com/sddai/p/8475424.html

https://blog.csdn.net/yywan1314520/article/details/50454063

https://www.cnblogs.com/pinking/p/8531405.html