CF335 ECounting Skyscrapers

Posted 2022-11-15 scx2015noip-as-php

题意

　　有一排高楼，每一栋高楼有一个正整数高度，高度为 \\(i\\) 的概率为 \\(2^-i\\)。一栋楼的每层从下往上依次编号为 \\(0,1,2,\\cdots,i-1\\)。
　　为了出题，大楼之间安装了溜索。在一栋楼的第 \\(i\\) 层和另一栋楼的第 \\(i\\) 层之间有一条溜索，当且仅当这两栋楼之间没有一栋大楼高度达到 \\(i\\) 层。
　　Alice 和 Bob 要数数有多少栋楼。
　　Alice 非常细心，她从最左侧的楼出发，计数器为 \\(1\\)。然后她向右移动，每经过一栋楼就将计数器 \\(+1\\)。
　　Bob 非常没耐心，他希望尽快数完。他从最左侧的楼出发，计数器为 \\(1\\)。他只使用溜索在大楼之间移动。Bob 会一直用最高的溜索向右移动，但由于恐高，他会忽略那些编号超过 \\(h\\) 的楼层。Bob 用溜索旅行跑得比香港记者还快，以至于他根本没法数清经过了多少栋楼，因此每经过一条溜索后只是将计数器 \\(+2^i\\)，其中 \\(i\\) 是这条溜索所在楼层的编号。
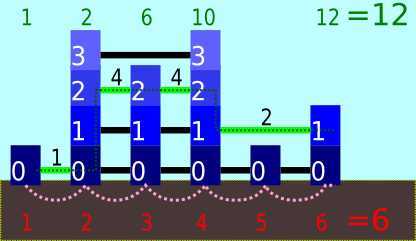
　　举个例子。有 \\(6\\) 栋大楼，从左到右的高度分别是 \\(1,4,3,4,1,2\\)，且 \\(h=2\\)。Alice 开始时计数器为 \\(1\\)，并且将计数器加了五次 \\(1\\)，得到的结果是 \\(6\\)。Bob 开始时计数器为 \\(1\\)，然后他依次加上 \\(1,4,4,2\\)，最终得到 \\(12\\)。注意，Bob 出于恐高忽略掉了最高的溜索。
　　
　　当 Alice 和 Bob 到达最右端的大楼时，他们将各自的计数器拿出来比较。给出 Alice 或者 Bob 的计数器的值，你需要计算出另外一个人的计数器的期望值。
　　\\(2\\le n\\le 30000,\\space 0\\le h\\le 30\\)

题解

　　二合一？

Bob

　　考虑一个子问题：\\(Bob\\) 每经过一条溜索，期望经过了多少栋楼。
　　设它的计数器累加了 \\(2^h\\)，即溜索所在楼层的编号是 \\(h\\)，高度是 \\(h+1\\)。那么中间那些楼的高度都必须 \\(\\le h\\)。
　　设每一栋楼的高度\\(\\le h\\) 的概率设为 \\(p\\)，题目说了高度为 \\(i\\) 的概率是 \\(2^-i\\)，则 \\[p=\\frac12+\\frac12^2+\\cdots+\\frac12^n=\\frac2^n-12^n=1-\\frac12^i\\]
　　那么从一栋高度 \\(\\ge h\\) 的楼的第 \\(h\\) 层出发走溜索，期望经过的高楼数就是 $$E=1\\times p(中间没有小楼)\\times p(最后一栋楼的高度