3.线性代数回顾

Posted 2022-11-13 weststar

3.1 矩阵和向量

如图：这个是4×2矩阵，即4行2列，m为行数，n为列数，那么m×n即4×2

 

 

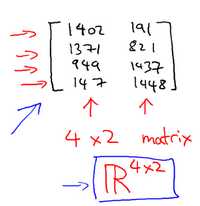
 矩阵的维数 即行数×列数

矩阵元素（矩阵项）：

 

 

 Aij指第??行，第??列的元素。

向量是一种特殊的矩阵，讲义中的向量一般都是列向量，如：

 

 

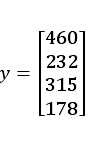
 如下图为 1 索引向量和 0 索引向量，左图为 1 索引向量，右图为 0 索引向量，一般我们用 1 索引向量。

 

 

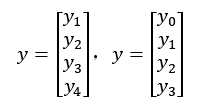
 3.2 加法和标量乘法

矩阵的加法：行列数相等的可以加。如：

 

 

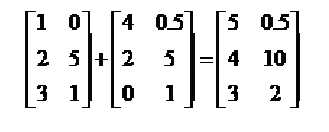
矩阵的乘法：每个元素都要乘 

 

 

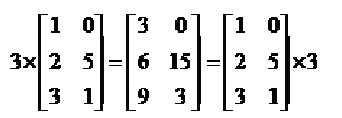
 3.3  矩阵向量乘法

矩阵和向量的乘法如图：?? × ??的矩阵乘以?? × 1的向量，得到的是?? × 1的向量

 

 

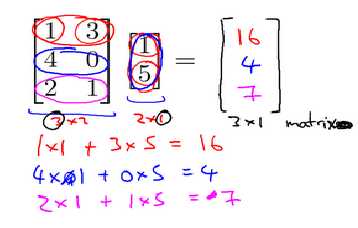
 3.4 矩阵乘法

矩阵乘法：
?? × ??矩阵乘以?? × ??矩阵，变成?? × ??矩阵。
如果这样说不好理解的话就举一个例子来说明一下，比如说现在有两个矩阵??和??，那
么它们的乘积就可以表示为图中所示的形式。

 

 

 

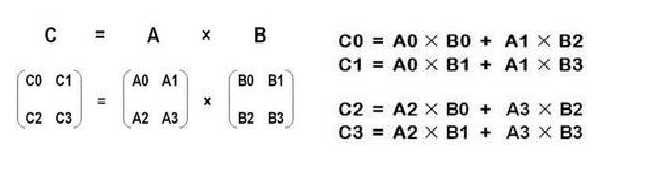
3.5  矩阵乘法的性质

矩阵乘法的性质：
矩阵的乘法不满足交换律：?? × ?? ≠ ?? × ??
矩阵的乘法满足结合律。即：?? × (?? × ??) = (?? × ??) × ??
单位矩阵：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的 1,我们称
这种矩阵为单位矩阵．它是个方阵，一般用 ?? 或者 ?? 表示，本讲义都用 ?? 代表单位矩阵，
从左上角到右下角的对角线（称为主对角线）上的元素均为 1 以外全都为 0。如：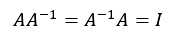

 

 

对于单位矩阵，有???? = ???? = ??

3.6 转置和逆矩阵

矩阵的逆：如矩阵??是一个?? × ??矩阵（方阵），如果有逆矩阵，则：????^(-1)= ??^(-1)A = ?? 

我们一般在 OCTAVE 或者 MATLAB 中进行计算矩阵的逆矩阵。
矩阵的转置：设??为?? × ??阶矩阵（即??行??列），第??行??列的元素是??(??, ??)，即：?? = ??(??, ??)
定义??的转置为这样一个?? × ??阶矩阵??，满足?? = ??(??, ??)，即 ??(??, ??) = ??(??, ??)（??的第??行
第??列元素是??的第??行第??列元素）记A^T =B(有些书记A‘=B)
直观来看，将??的所有元素绕着一条从第 1 行第 1 列元素出发的右下方 45 度的射线作
镜面反转，即得到??的转置。