图形学中的噪声入门

Posted 2022-11-13 afuness

一、白噪声

白噪声常与伪随机数一起使用。这样，固定的输入就会产出固定的随机数输出，最终渲染出来的纹理也会是固定的，但又具备随机的视觉效果。

常用的白噪声随机产生函数如下：

float random = dot(vec in , vec const);

使用输入向量和一个任意向量点乘，即可得到一个随机的结果；

在OpenGL中使用：

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform float u_time;

float rand(vec2 vec)
    float random = dot(vec , vec2(-12.000,20.820));
    random = fract(random);
    return random;


void main() 
    vec2 uv = gl_FragCoord.xy/u_resolution.yy;
    vec3 color = vec3(rand(uv));
    gl_FragColor = vec4(color,1.0);

得到的噪声图：

 

 可以看到两个向量点乘投影形成的条带。一点也不均匀。

解决方法是对点积后的结果取正弦，然后乘上一个大数，将其小数点移后几位，得到更为随机分布的小数。

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform float u_time;

float rand(vec2 vec)
    float random = sin(dot(vec, vec2(12.9898,78.233))) * 43758.5453;
    random = fract(random);
    return random;


void main() 
    vec2 uv = gl_FragCoord.xy/u_resolution.yy;
    vec3 color = vec3(rand(uv));
    gl_FragColor = vec4(color,1.0);

得到的噪声如下：

 

 注意这里取的

vec2(12.9898,78.233)

和43758.5453;

都是前辈们总结下来的经验数，可以得到很好的白噪声图。

二、细胞

分割为细胞的方法就是纹理坐标乘上对应的倍数，简单高效。

void main() 
    vec2 uv = gl_FragCoord.xy/u_resolution.yy;
    uv  = uv * 10.0;
    
    vec3 color = vec3(fract(uv),1.0);
    gl_FragColor = vec4(color,1.0);

得到的效果图：

 

 为每个细胞赋上不同的颜色：

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;

float rand2dTo1d(vec2 value ,vec2 randvec2 )

    vec2 dotDir = randvec2;
    vec2 smallValue = sin(value);
    float random = dot(smallValue, dotDir);
    random = fract(sin(random) * 143758.5453);
    return random;


vec2 rand2dto2d(vec2 value)
     return vec2(
        rand2dTo1d(value, vec2(12.989, 78.233)),
        rand2dTo1d(value, vec2(39.346, 11.135))
    );


void main() 
    vec2 uv = gl_FragCoord.xy/u_resolution.yy;
    vec2 st  = uv * 10.0;
    

    vec3 color = vec3(rand2dto2d(floor(st)),1.0);
    gl_FragColor = vec4(color,1.0);

得到的图片：

 

 这里使用了前面提到的白噪声公式来为细胞产出不同的颜色。

三、柏林噪声

白噪声很好，但是它不具备连续性。

柏林噪声可以很好地解决这个问题。

使用一维柏林噪声：

使用一维的白噪声生成灰度图

float rand1dTo1d(float value)
    float mutator = 0.546;
    float random = fract(sin(value + mutator) * 143758.5453);
    return random;


void main() 
    vec2 uv = gl_FragCoord.xy/u_resolution.yy;

    vec3 color = vec3(rand1dTo1d( floor(uv.x * 30.)));
    gl_FragColor = vec4(color,1.0);

得到：

 

将其压缩成线：

float rand1dTo1d(float value)
    float mutator = 0.546;
    float random = fract(sin(value + mutator) * 143758.5453);
    return random;


void main() 
    vec2 uv = gl_FragCoord.xy/u_resolution.yy;
    
    //移到中心
    uv -= vec2(0.5);
    vec2 st = uv * 6.;
    
    
    float noise = rand1dTo1d( floor(st.x));
    
　　//取噪声与纹理y坐标距离
　　//在 dist-> 0时画线,
    float dist = abs(noise - st.y);

　　//抗锯齿
    vec3 color = vec3(smoothstep(0, fwidth(st.y), dist));
    
    gl_FragColor = vec4(color,1.0);

得到：

 

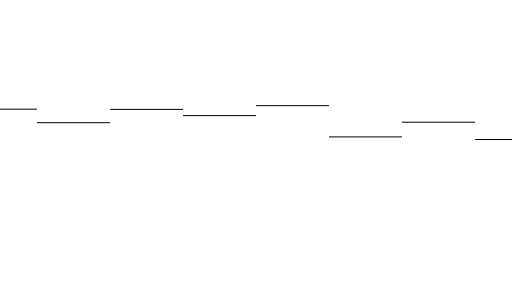
 为了让值连续，取其小数部分进行插值，修改noise如下：

//插值
    float noise = mix(rand1dTo1d( floor(st.x)), rand1dTo1d(ceil(st.x)), fract(st.x));

得到的图如下：

 

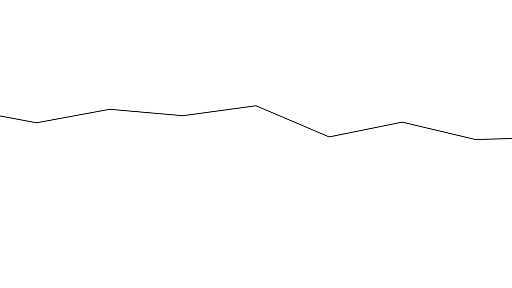
 这时使用的插值因子是

st.x

得到的结果并不平滑，我们应该使用缓动公式插值，常见的公式是。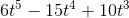

更改，如下：

    //插值
    float x = fract(st.x);
    float t= 6.*pow(x,5.) - 15.*pow(x,4.)+10.*pow(x,3.);
    float noise = mix(rand1dTo1d( floor(st.x)), rand1dTo1d(ceil(st.x)), fract(t));

得到的图如下：

 

 此时，一个连续的一维的噪声就生成了。

下面应用到二维：

一张纹理图片中，直观输入就是uv，一个vec2变量。