数据挖掘算法：DBSCAN算法的C++实现

Posted 2020-07-30 LZ_Jaja

(期末考试快到了，所以比较粗糙，请各位读者理解。。)

一、    概念

DBSCAN是一种产生划分聚类的基于密度的聚类算法，簇的个数由算法自动地确定。低密度区域中的点被视为噪声而忽略，因此DBSCAN不产生完全聚类。

二、    伪代码

1    将所有点标记为核心点、边界点和噪声点。

2    删除噪声点。

3    为距离在Eps之内的所有核心点之间赋予一条边。

4    每组连通的核心点形成一个簇。

5    将每个边界点指派到一个与之关联的核心点的簇中。

三、    重要数据结构

1    定义邻域半径值、密度阈值、数据集点数

#define Eps 3 // Eps为邻域半径值

#define MinPts 3  // 邻域密度阈值

#define N 20  // 数据集包含N个对象

2    定义数组保存所有点

double point[N][2];      // 保存所有的数据点

3    定义vector保存核心点、边界点、噪声点的位置

vector<int> kernel_point;   // 保存核心点在point[][]中的位置

vector<int> border_point;   // 保存边界点在point[][]中的位置

vector<int> noise_point; // 保存噪声点在point[][]中的位置

4    定义vector保存最终形成的簇

vector<vector<int> > cluster;   // 保存最终形成的簇，每个簇中包含点在point[][]中的位置

四、    源代码

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <vector>
#include <cmath>

using namespace std;

#define Eps 3 // Eps为邻域半径值
#define MinPts 3 // 邻域密度阈值
#define N 20 // 数据集包含N个对象

double point[N][2]; // 保存所有的数据点
vector<int> kernel_point; // 保存核心点在point[][]中的位置
vector<int> border_point; // 保存边界点在point[][]中的位置
vector<int> noise_point; // 保存噪声点在point[][]中的位置
vector<vector<int> > mid; // 可能存在重叠的簇
vector<vector<int> > cluster; // 保存最终形成的簇，每个簇中包含点在point[][]中的位置

// 初始化N个坐标点
void init(int n) {
srand((unsigned)time(NULL));
for(int i=0; i<n; i++) {
for(int j=0; j<2; j++) {
point[i][j] = rand() % (N+1);
}
}
}

int main(int argc, char** argv) {

// 初始化数据集
int n = N;
init(n);

// 将所有点标记为核心点、边界点或噪声点
// 标记核心点
for(int i=0; i<N; i++) {
int num = 0; // 判断是否超过MinPts，若一次循环后num>=MinPts，则加入核心点
for(int j=0; j<N; j++) {
if(pow(point[i][0]-point[j][0], 2)+pow(point[i][1]-point[j][1], 2)<=pow(Eps, 2)) { // 本身也算一个
num++;
}
}
if(num>=MinPts) {
kernel_point.push_back(i);
}
}

// 标记为边界点或噪声点
for(int i=0; i<N; i++) {
// 边界点或噪声点不能是核心点
int flag = 0; // 若flag=0，则该点不是核心点，若flag=1，则该点为核心点
for(int j=0; j<kernel_point.size(); j++) {
if(i == kernel_point[j]) {
flag = 1;
break;
}
}
if(flag == 0) {
// 判断是边界点还是噪声点
int flag2 = 0; // 若flag=0，则该点为边界点，若flag=1，则该点位噪声点
for(int j=0; j<kernel_point.size(); j++) {
int s = kernel_point[j]; // 标记第j个核心点在point[][]中的位置，方便调用
if(pow(point[i][0]-point[s][0], 2)+pow(point[i][1]-point[s][1], 2)<pow(Eps, 2)) {
flag2 = 0;
border_point.push_back(i);
break;
}
else {
flag2 = 1;
continue;
}
}
if(flag2 == 1) {
// 加入噪声点
noise_point.push_back(i);
continue;
}
}
else {
continue;
}
}

// 将距离在Eps之内的核心点放在一个vector中
for(int i=0; i<kernel_point.size(); i++) {
int x = kernel_point[i];
vector<int> record; // 对于每一个点建立一个record，放入mid当中
record.push_back(x);
for(int j=i+1; j<kernel_point.size(); j++) {
int y = kernel_point[j];
if(pow(point[x][0]-point[y][0], 2)-pow(point[x][1]-point[y][1], 2)<pow(Eps, 2)) {
record.push_back(y);
}
}
mid.push_back(record);
}

// 合并vector
for(int i=0; i<mid.size(); i++) { // 对于mid中的每一行
// 判断该行是否已经添加进前面的某一行中
if(mid[i][0] == -1) {
continue;
}
// 如果没有被判断过
for(int j=0; j<mid[i].size(); j++) { // 判断其中的每一个值
// 对每一个值判断其他行中是否存在
for(int x=i+1; x<mid.size(); x++) { // 对于之后的每一行
if(mid[x][0] == -1) {
continue;
}
for(int y=0; y<mid[x].size(); y++) {
if(mid[i][j] == mid[x][y]) {
// 如果有一样的元素，应该放入一个vector中，并在循环后加入precluster，同时置该vector内所有元素值为-1
for(int a=0; a<mid[x].size(); a++) {
mid[i].push_back(mid[x][a]);
mid[x][a] = -1;
}
break;
}
}
}
}

cluster.push_back(mid[i]);

}

// 删除cluster中的重复元素
for(int i=0; i<cluster.size(); i++) { // 对于每一行
for(int j=0; j<cluster[i].size(); j++) {
for(int n=j+1; n<cluster[i].size(); n++) {
if(cluster[i][j] == cluster[i][n]) {
cluster[i].erase(cluster[i].begin()+n);
n--;
}
}
}
}

// 至此，cluster中保存了各个簇，每个簇中有点对应在point[][]中的位置
// 将每个边界点指派到一个与之相关联的核心点的簇中
for(int i=0; i<border_point.size(); i++) { // 对于每一个边界点
int x = border_point[i];
for(int j=0; j<cluster.size(); j++) { // 检查每一个簇，判断边界点与哪个簇中的核心点关联，将边界点加入到第一个核心点出现的簇中
int flag = 0; // flag=0表示没有匹配的项，flag=1表示已经匹配，退出循环
for(int k=0; k<cluster[j].size(); k++) {
int y = cluster[j][k];
if(pow(point[x][0]-point[y][0], 2)+pow(point[x][1]-point[y][1], 2)<pow(Eps, 2)) {
cluster[j].push_back(x);
flag = 1;
break;
}
}
if(flag == 1) {
break;
}
}
}


/*******************************************************************************************/
cout<<"All Points : "<<endl;
for(int i=0; i<N; i++) {
cout<<"第"<<i<<"个"<<"\\t";
for(int j=0; j<2; j++) {
cout<<point[i][j]<<"\\t";
}
cout<<endl;
}
cout<<endl;

cout<<"Kernel Points : "<<endl;
for(int i=0; i<kernel_point.size(); i++) {
cout<<kernel_point[i]<<"\\t";
}
cout<<endl<<endl;

cout<<"Border Points : "<<endl;
for(int i=0; i<border_point.size(); i++) {
cout<<border_point[i]<<"\\t";
}
cout<<endl<<endl;

cout<<"Noise Points : "<<endl;
for(int i=0; i<noise_point.size(); i++) {
cout<<noise_point[i]<<"\\t";
}
cout<<endl<<endl;

cout<<"Cluster : "<<endl;
for(int i=0; i<cluster.size(); i++) {
cout<<"第"<<i<<"个"<<"\\t";
for(int j=0; j<cluster[i].size(); j++) {
cout<<cluster[i][j]<<"\\t";
}
cout<<endl;
}

return 0;
}

五、    运行结果

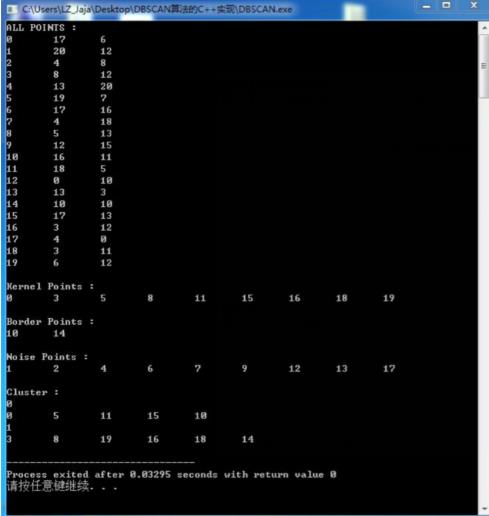
图1 DBSCAN算法的运行结果

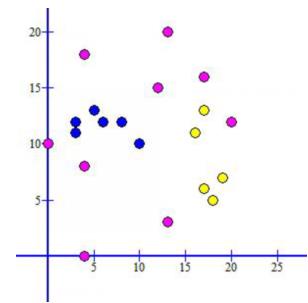
图2 利用Graph作图展示DBSCAN算法运行结果

（其中，粉色点为噪声点，蓝色与黄色为两个簇）