二叉搜索树

Posted 2022-11-05 nickchen121

目录

• 一、什么是二叉搜索树
• 二、二叉搜索操作的特别函数：
• 三、二叉查找树的查找操作：Find
• 四、查找最大和最小元素
• 五、二叉搜索树的插入
• 六、二叉搜索树的删除
  • 6.1 删除的是叶结点
  • 6.2 删除的结点只有一个孩子结点
  • 6.3 删除的结点有左右子树
• 七、Python递归实现-二叉搜索树

更新、更全的《数据结构与算法》的更新网站，更有python、go、人工智能教学等着你：https://www.cnblogs.com/nickchen121/p/11407287.html

一、什么是二叉搜索树

首先让我们回顾之前说过的查找问题：上次我们之讲过了静态查找，这次我们将通过二叉搜索树实现动态查找。但是针对动态查找，数据该如何组织呢？

二叉搜索树（BST，Binary Search Tree），也称二叉排序树或二叉查找树

二叉搜索树：一颗二叉树，可以为空；如果不为空，满足以下性质：

1. 非空左子树的所有键值小于其根节点的键值
2. 非空右子树的所有键值大于其根节点的键值
3. 左、右子树都是二叉搜索树

二、二叉搜索操作的特别函数：

Position Find(ElementType X, BinTree BST)：从二叉搜索树BST中查找元素X，返回其所在结点的地址；

Postion FindMin(BinTree BST)：从二叉搜索树BST中查找并返回最小元素所在结点的地址；

Postion FindMax(BinTree BST)：从二叉搜索树BST中查找并返回最大元素所在结点的地址；

BinTree Insert(ElementType X, BinTree BST)

BinTree Delete(ElementType X, BinTree BST)

三、二叉查找树的查找操作：Find

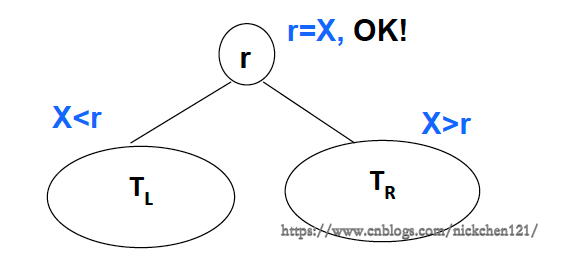
• 查找从根节点开始，如果树为空，返回NULL
• 若搜索树非空，则根节点关键字和X进行比较，并进行不同处理：
  • 若X小于根节点键值，只需在左子树中继续搜索
  • 如果X大于根节点的键值，在右子树中进行继续搜索
  • 若两者比较结果是相等，搜索完成，返回指向此结点的指针

/* c语言实现 */

Position Find(ElementType X, BinTree BST)

  if (!BST) return NULL; // 查找失败
  if (X > BST->Data)
    return Find(X, BST->Right); // 在右子树中继续查找 // 尾递归
  else if (X < BST->Data)
    return Find(X, BST->Left); // 在左子树中继续查找 // 尾递归
  else // X == BST->Data
    reutrn BST; // 查找成功，返回结点的找到结点的地址

# python语言实现

def find(self, root, val):
  '''二叉搜索树查询操作'''
  if root == None:
    return False
  if root.val == val:
    return True
  elif val < root.val:
    return self.query(root.left, val)
  elif val > root.val:
    return self.query(root.right, val)

由于上述非递归函数的执行效率高，可将“尾递归”函数改为迭代函数

/* c语言实现 */

Position IterFind(ElementType X, BinTree BST)

  while (BST)
    if (X > BST->Data)
      BST = BST->Right; // 向右子树中移动，继续查找
    else if (X < BST->Data)
      BST = BST->Left; // 向左子树中移动，继续查找
    else // X == BST->Data
      return BST; // 查找成功，返回结点的找到结点的地址
  
  reuturn NULL; // 查找失败

# python语言实现

def iter_find(self, root, val):
        '''二叉搜索树查询操作'''
    while root:
        if root.val == val:
            return root
        elif val < root.val:
            root = root.left
        elif val > root.val:
            root = root.right
        if root == None:
                return False

查找效率决定于树的高度

四、查找最大和最小元素

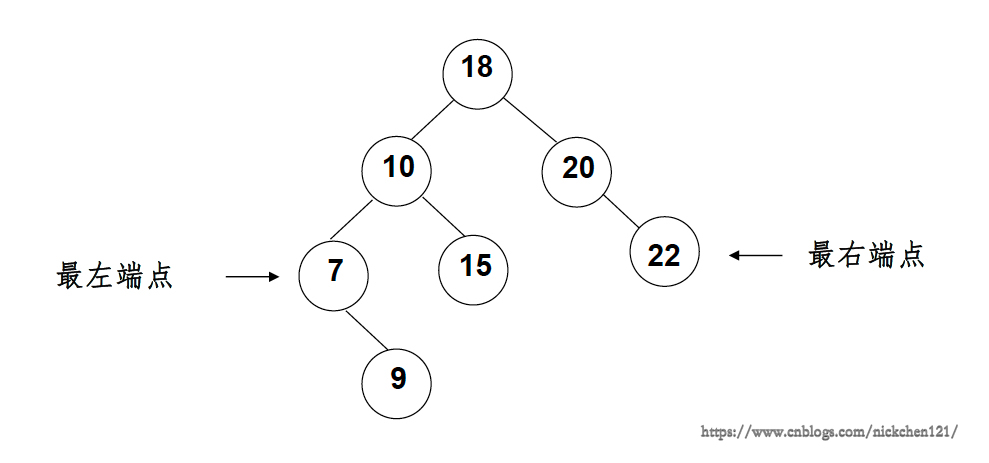
• 从根节点开始，沿着右子树一直往下，直到找到最后一个右子树节点，最大元素一定是在树的最右分支的端结点上
• 从根节点开始，沿着左子树一直往下，直到找到最后一个左子树节点，最小元素一定是在树的最左分支的端结点上

/* c语言实现 */

// 查找最小元素的递归函数
Position FindMin(BinTree BST)

  if (!BST) return NULL; // 空的二叉搜索树，返回NULL
  else if (!BST->Left)
    reuturn BST; // 找到最左叶结点并返回
  else
    return FindMin(BST->Left); // 沿左分支继续查找

  
// 查找最大元素的迭代函数
Postion FindMax(BinTree BST)

  if (BST)
    while (BST->Right) BS = BST->Right; // 沿右分支继续查找，直到最右叶结点
  return BST;

# python语言实现

# 查找最小值
def findMin(self, root):
        '''查找二叉搜索树中最小值点'''
        if root.left:
            return self.findMin(root.left)
        else:
            return root

# 查找最大值
def findMax(self, root):
        '''查找二叉搜索树中最大值点'''
        if root.right:
            return self.findMax(root.right)
        else:
            return root

五、二叉搜索树的插入

分析：关键是要找到元素应该插入的位置，可以采用与Find类似的方法。

/* c语言实现 */

BinTree Insert(ElementType X, BinTree BST)

  if (!BST) // 若原树为空，生成并返回一个结点的二叉搜索树
    BST = malloc(sizeof(struct TreeNode));
    BST->Data = X;
    BST->Left = BST->Right = NULL;
  else // 开始找要插入元素的位置
    if (X < BST->Data)
      BST->Left = Insert(X, BST->Left); // 递归插入左子树
    else if (X > BST->Data)
      BST->Right = Insert(X, BST->Right); // 递归插入右子树
        // else X已经存在，什么都不做
  return BST;

# python语言实现

def insert(self, root, val):
        '''二叉搜索树插入操作'''
        if root == None:
            root = TreeNode(val)
        elif val < root.val:
            root.left = self.insert(root.left, val)
        elif val > root.val:
            root.right = self.insert(root.right, val)
        return root

例：以一年十二个月的英文缩写为键值，按从一月到十二月顺序输入（以第一个字母、第二个字母的顺序），即输入序列为（Jan, Feb, Mar, Apr, May, Jun, July, Aug, Sep, Oct, Nov, Dec）

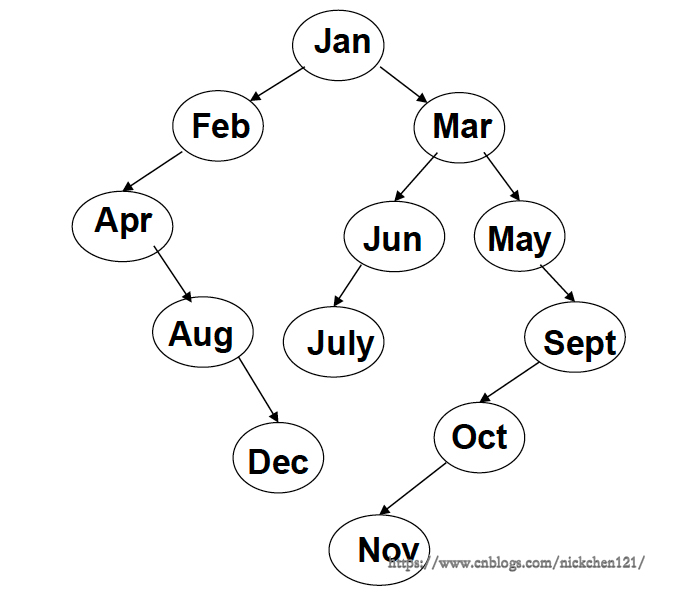
六、二叉搜索树的删除

考虑三种情况

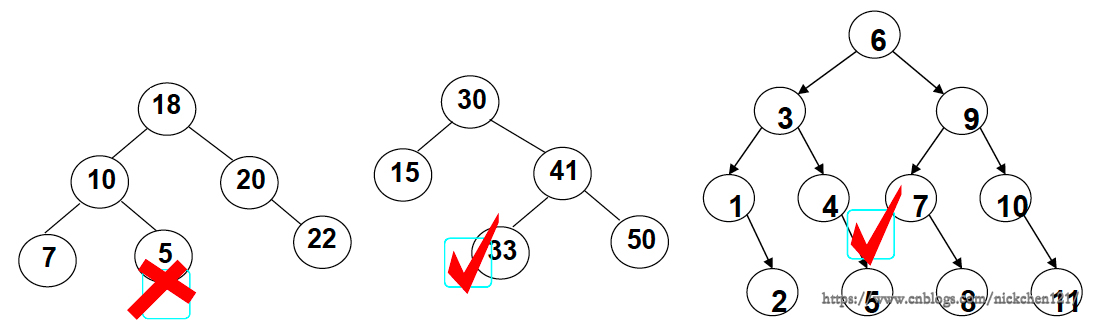
6.1 删除的是叶结点

直接删除，并再修改其父结点指针——置为NULL

以删除35举例：

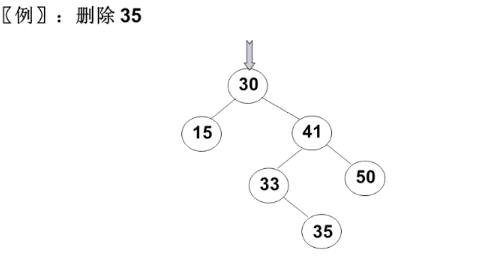
6.2 删除的结点只有一个孩子结点

以删除33举例

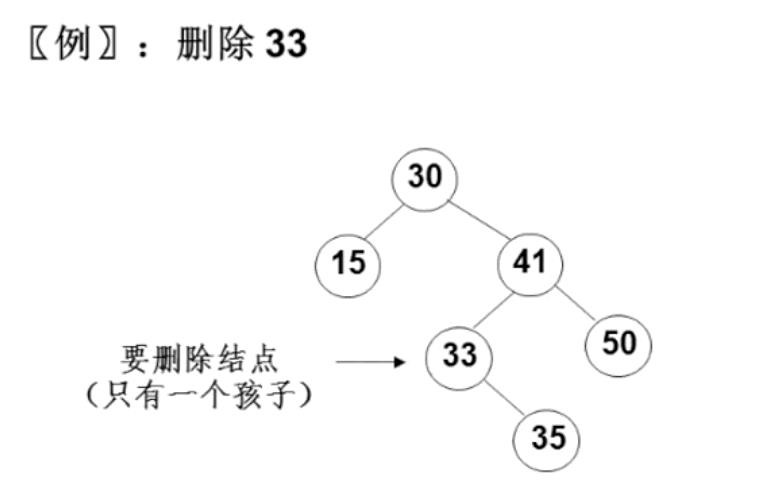
6.3 删除的结点有左右子树

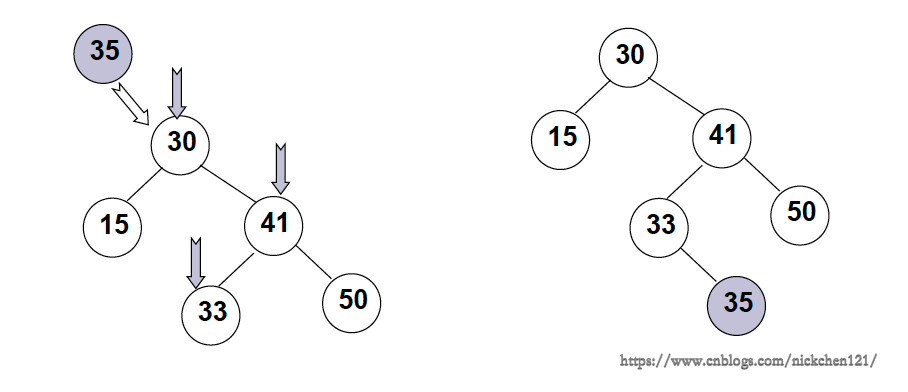
用另一结点替代被删除结点：右子树的最小元素或者左子树的最大元素

以删除41举例

下图为右子树的最小元素替代：

下图为左子树的最大元素替代：

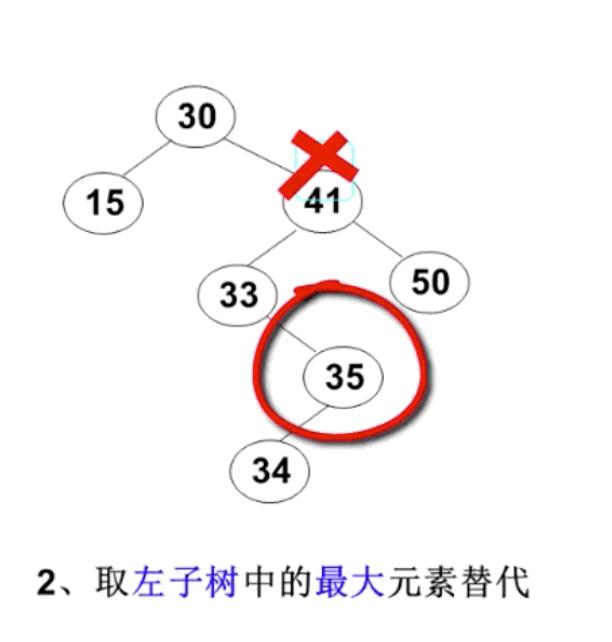
/* c语言实现 */

BinTree Delete(ElementType X, BinTree BST)

  Position Tmp;
  if (!BST) printf("要删除的元素未找到");
  else if (X < BST->Data)
    BST->Left = Delete(X, BST->Left); // 左子树递归删除
  else if (X > BST->Data)
    BST->Right = Delete(X, BST->Right); // 右子树递归删除
  else // 找到要删除的结点
    if (BST->Left && BST->Right) // 被删除结点有左右两个子结点
      Tmp = FindMin(BST->Right); // 在右子树中找最小的元素填充删除结点
      BST->Data = Tmp->Data;
      BST->Right = Delete(BST->Data, BST->Right); // 在删除结点的右子树中删除最小元素
     else  // 被删除结点有一个或无子结点
      Tmp = BST;
      if (!BST->Left)
        BST = BST->Right; // 有右孩子或无子结点
      else if (!BST->Right) 
        BST = BST->Left; // 有左孩子或无子结点
      fee(Tmp);
    
  return BST;

# python语言实现

def delNode(self, root, val):
        '''删除二叉搜索树中值为val的点'''
        if root == None:
            return 
        if val < root.val:
            root.left = self.delNode(root.left, val)
        elif val > root.val:
            root.right = self.delNode(root.right, val)
        # 当val == root.val时，分为三种情况：只有左子树或者只有右子树、有左右子树、即无左子树又无右子树
        else:
            if root.left and root.right:
                # 既有左子树又有右子树，则需找到右子树中最小值节点
                temp = self.findMin(root.right)
                root.val = temp.val
                # 再把右子树中最小值节点删除
                root.right = self.delNode(root.right, temp.val)
            elif root.right == None and root.left == None:
                # 左右子树都为空
                root = None
            elif root.right == None:
                # 只有左子树
                root = root.left
            elif root.left == None:
                # 只有右子树
                root = root.right
        return root

七、Python递归实现-二叉搜索树

# python语言实现

class Node(object):
    def __init__(self, element):
        self.element = element
        self.lchild = None
        self.rchild = None


class Tree(object):
    def __init__(self, root=None):
        self.root = root

    def add(self, cur, item):
        if item < cur.element:
            if cur.lchild:
                self.add(cur.lchild, item)
            else:
                cur.lchild = Node(item)
        else:
            if cur.rchild:
                self.add(cur.rchild, item)
            else:
                cur.rchild = Node(item)