Floyd-Warshall Algorithm

Posted 2022-11-03 hankunyan

The Floyd Warshall Algorithm is for solving the All Pairs Shortest Path problem. The problem is to find the shortest distances between every pair of vertices in a given edge-weighted directed Graph.

One approach would be to execute our general shortest-path algorithm Bellman-Ford Algorithm (since there may be negative edges) |V| times, once for each starting node. The total running time would then be O(|V|^2*|E|). We’ll now see a better alternative, the O(|V|^3) dynamic programming-based Floyd-Warshall algorithm.

Suppose number the vertices in V as 1, 2, . . . , n, and let dist(i, j, k) denote the length of the shortest path from i to j in which only nodes 1, 2, . . . , k can be used as intermediates. Initially, dist(i, j, 0) is the length of the direct edge between i and j, if it exists, and is ∞ otherwise.

What happens when we expand the intermediate set to include an extra node k? We must reexamine all pairs i, j and check whether using k as an intermediate point gives us a shorter path from i to j. But this is easy: a shortest path from i to j that uses k along with possibly other lower-numbered intermediate nodes goes through k just once (why? because we assume that there are no negative cycles). And we have already calculated the length of the shortest path from i to k and from k to j using only lower-numbered vertices:

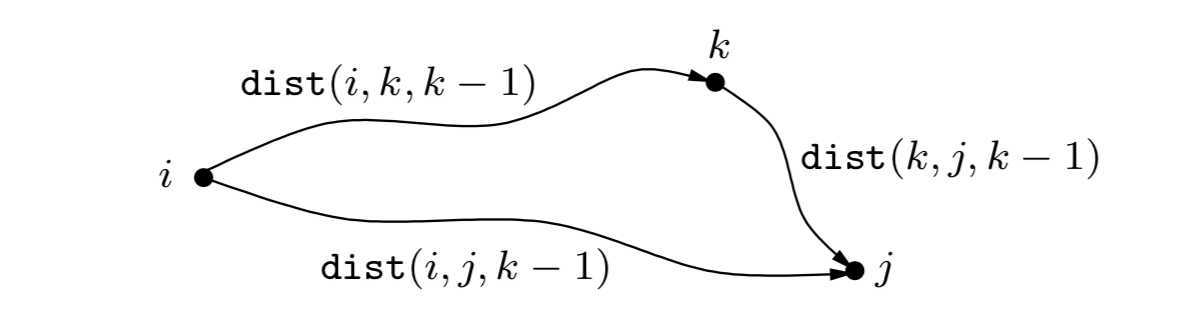
Thus, using k gives us a shorter path from i to j if and only if

dist(i,k,k−1) + dist(k,j,k−1) < dist(i,j,k−1)

in which case dist(i, j, k) should be updated accordingly.

Here is the Floyd-Warshall algorithm—and as you can see, it takes O(|V|^3) time. 

An honest implementation of the above rule would involve a 3-dimensional array, dist[i, j, k]. However, a careful analysis of the algorithm reveals that the third dimension does not need to be explicitly stored. We will present the simpler version of the algorithm (which omits the kth dimension).

Proof: Notice dist[i,j,k] depends on dist[i,k,k−1], dist[k,j,k−1] and dist[i,j,k−1]. The kth column and kth row of matrix dist will remain the same in this iteration, because dist[k,j] and dist[i,k] cannot achieve a smaller distance when node k is added. Thus, we can omit the third dimension in dp.

#define V 4  
#define INF 99999  

vector<vector<int>> floydWarshall(int graph[][V])
    vector<vector<int>> dist(V,vector<int>(V));
    for (int i=0;i<V;++i)
        for (int j=0;j<V;++j)
            dist[i][j] = graph[i][j];
    // the shortest distances consider only the vertices in set 0, 1, 2, .. k-1 as intermediate vertices.
    for (int k=0;k<V;++k)
        for (int i=0;i<V;++i)
            for (int j=0;j<V;++j)
                if (dist[i][k]+dist[k][j]<dist[i][j])
                    dist[i][j] = dist[i][k]+dist[k][j];
            
        
    
    return dist;


int main()    
    /* Let us create the following weighted graph  
         10  
    (0)------->(3)  
     |       /|\\  
   5 |        |  
     |        | 1  
    \\|/       |  
    (1)------->(2)  
          3         */
    int graph[V][V] =  0, 5, INF, 10,  
                        INF, 0, 3, INF,  
                        INF, INF, 0, 1,  
                        INF, INF, INF, 0 ;  
    auto dist=floydWarshall(graph);
    for (int i=0;i<V;++i)
        for (int j=0;j<V;++j)
            cout << dist[i][j] << ‘ ‘;
        cout << endl;
    
    return 0;  
  

时间复杂度 O(V^3) 

 

Reference

https://www.geeksforgeeks.org/floyd-warshall-algorithm-dp-16/

http://www.cs.umd.edu/class/fall2017/cmsc451-0101/Lects/lect13-dp-floyd.pdf