中心极限定理|z分布|t分布|卡方分布
Posted yuanjingnan
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了中心极限定理|z分布|t分布|卡方分布相关的知识,希望对你有一定的参考价值。
生物统计学
抽样分布:n个样本会得到n个统计量,将这n个统计量作为总体,该总体的分布即是抽样分布
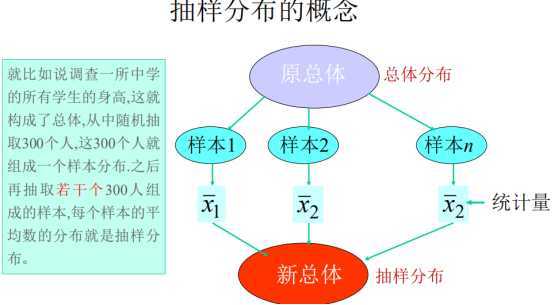
根据辛钦大数定律,从一个非正态分布的总体中抽取的含量主n的样本,当n充分大时,样本平均数渐近服从正态分布。因此平均数的抽样分布对正态性的要求并不是十分严格,但方差的抽样分布,对总体的正态性的要求是十分严格的。
样本平均值的分布:
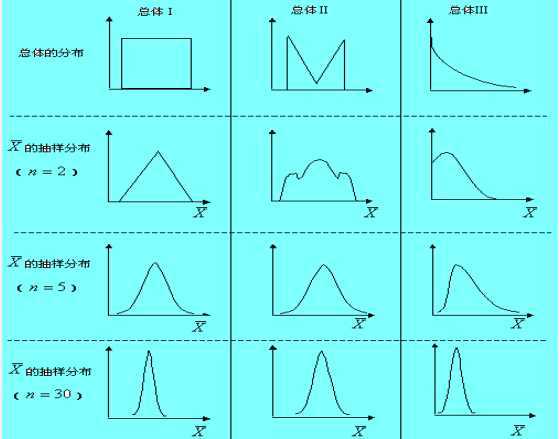
基于正态总体(两个参数都知道)的抽样分布:
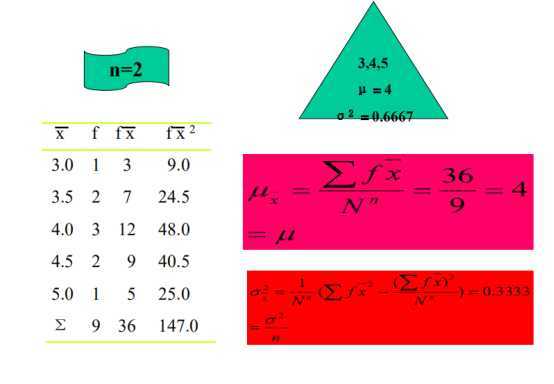
eg‘:总体n=3,
因为n=2有放回抽样,有9种可能性:
n=4有放回抽样,有81种可能性
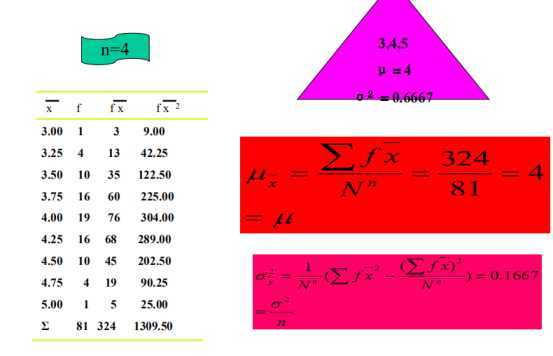
统计量与总体参数不完全一样,但是满足以上关系,所以有:

标准误就是参数方差
非正态分布总体(两个参数都知道):根据中心极限定理,大样本同基于正态总体
所以,只要是大样本都会满足z分布,z即满足N(0,1)

方差未知:用样本标准差代替总体标准差,并得到t,此时是t满足自由度为(n-1)的t分布,从PDF可知t分布只与自由度有关,与其他无关。
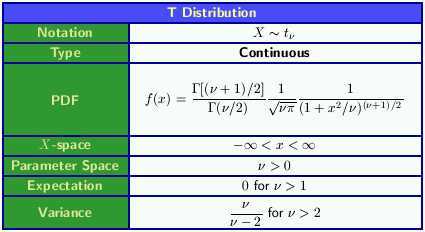
因为n个数要满足均数,必有一个数的值受其他数影响,又因为自由度是独立观测的个数,所以自由度为n-1:
当自由度较大时,也就是n较大时就是正态分布;t--->u
特征值:
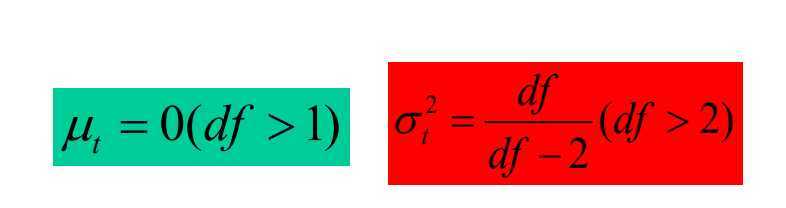
总体分布和抽样分布的关系:
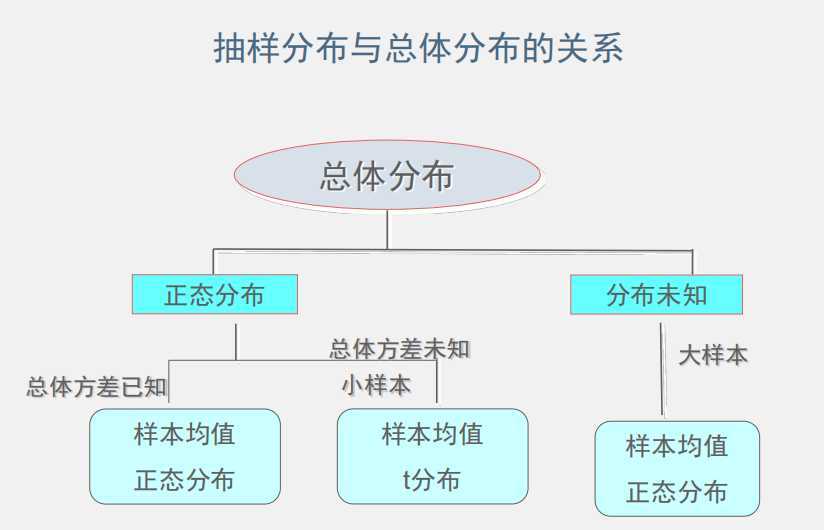
PS:对于总体分布未知的小样本并无方法
样本方差的分布
正态总体时,两个参数都知道的情况下,样本方差满足卡方分布

随机变量是S方,所以卡方也是一个随机变量,卡方分布只与自由度有关系。
总结:
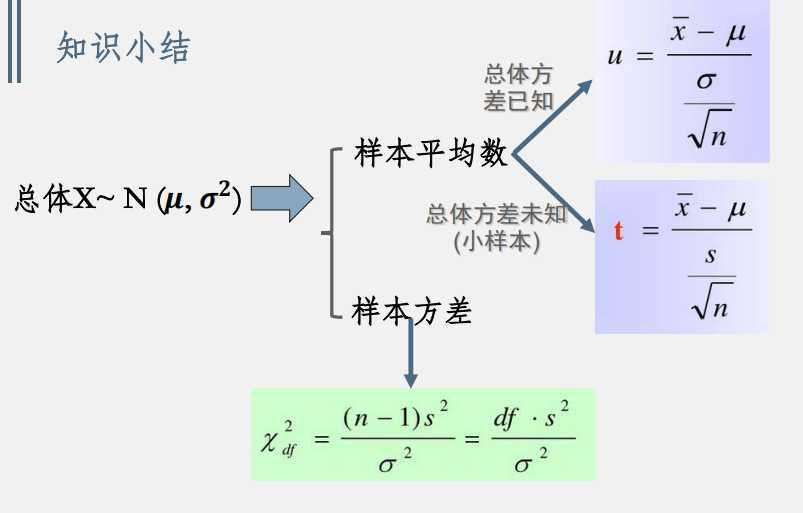
两个正态分布总体(都知道均数和方差),两个样本平均数的和与差的分布:利用正态分布加加减减
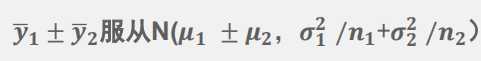
两个正态分布总体(都知道均数,但未知方差具体值,但知道方差相等),两个样本平均数的和与差的分布:利用他分布加加减减
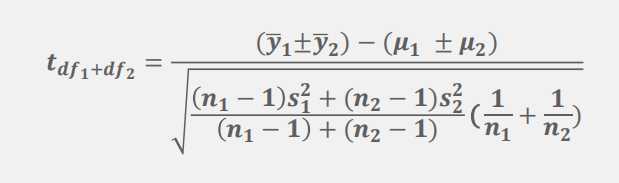
分布使用条件:1.均值是否已知?2.方差是否已知?3.样本量是大或者小?
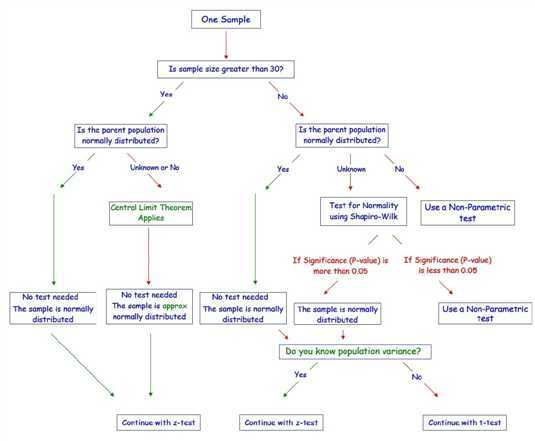
以上是关于中心极限定理|z分布|t分布|卡方分布的主要内容,如果未能解决你的问题,请参考以下文章