未知来源玩具谜题

Posted 2022-10-31 scx2015noip-as-php

题意

　　有 \\(n\\) 个数，你需要给每个数涂上红色或蓝色，使得任意两个红色的数不小于一个常数 \\(A\\)，且任意两个蓝色的数不小于一个常数 \\(B\\)。求方案数。
　　\\(n\\le 10^5\\)
　　\\(1\\le A,B,a_i\\le 10^18\\)
　　\\(a_i\\lt a_i+1\\)

题解

solution 1

　　首先有个小学生都会写的 \\(30\\) 分暴力 \\(\\textdp\\)：设 \\(dp(j,k)\\) 表示涂完前 \\(i\\) 个数后，最后一个红数在第 \\(j\\) 位，最后一个蓝数在第 \\(k\\) 位。
　　显然状态中不用记 \\(i\\)，因为 \\(\\max(j,k)=i\\)。

#include<bits/stdc++.h>
#define ll long long
#define N 2005
#define mod 1000000007
using namespace std;
inline ll read()
    ll x=0; bool f=1; char c=getchar();
    for(;!isdigit(c); c=getchar()) if(c=='-') f=0;
    for(; isdigit(c); c=getchar()) x=(x<<3)+(x<<1)+(c^'0');
    if(f) return x;
    return 0-x;

ll n,a,b,p[N];
int dp[N][N];
int main()
    n=read(), a=read(), b=read();
    if(n>2000)puts("0"); return 0;
    for(int i=1; i<=n; ++i) p[i]=read();
    dp[0][1]=dp[1][0]=1;
    for(int i=2; i<=n; ++i)
        if(i-1==0 || p[i]-p[i-1]>=a) for(int j=0; j<=i-2; ++j) (dp[i][j]+=dp[i-1][j])%=mod;
        if(i-1==0 || p[i]-p[i-1]>=b) for(int j=0; j<=i-2; ++j) (dp[j][i]+=dp[j][i-1])%=mod;
        for(int j=0; j<=i-2; ++j)
            if(!j || p[i]-p[j]>=a) (dp[i][i-1]+=dp[j][i-1])%=mod;
            if(!j || p[i]-p[j]>=b) (dp[i-1][i]+=dp[i-1][j])%=mod;
        
    
    int ans=0;
    for(int i=0; i<=n; ++i) (ans+=((dp[n][i]+dp[i][n])%mod))%=mod; 
    cout<<ans<<endl;
    return 0;

　　然后我们发现这个转移好像就是一堆数组平移。
　　我们把 \\(\\textdp(i,j)\\) 的矩阵画出来

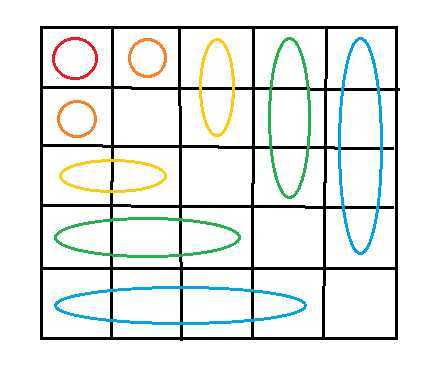
　　一种颜色圈的区间对应一个 \\(i\\)。\\(j=i\\) 和 \\(k=i\\) 对应两个不相交的一维数组。
　　所以我们可以把 \\(\\textdp\\) 的两维拆成两个数组分开处理。考虑预处理出每个前缀 \\([1,i]\\) 中最后一个满足 \\(a_i-a_r\\ge A\\) 的 \\(r\\) 和最后一个满足 \\(a_i-a_b\\ge B\\) 的 \\(b\\)，则暴力代码可以改写为

　　\\(query(x,y)\\) 表示求 \\(x\\) 数组第 \\(0\\) 到 \\(y\\) 位的和。
　　我们发现问题简化成了支持两个数组的整体平移、区间求和、单点修改。
　　主席树维护即可。复杂度 \\(O(n\\log n)\\)。

solution 2

　　一个与暴力无关的做法。
　　考虑从大到小钦定每个数为红色还是蓝色。
　　若 \\(a_n\\) 涂了红色，那么 \\(a_n-1,a_n-2,\\cdots\\) 等数就必须涂蓝色。

　　比如有 \\(6\\) 个数：3 4 7 8 9 11
　　\\(A=3,\\space B=4\\)
　　如果把 \\(11\\) 涂成红色，那么 \\(8,9\\) 就必须涂成蓝色。
　　而把 \\(8,9\\) 涂成蓝色，\\(7\\) 就必须涂成红色。
　　但是 \\(7\\) 和 \\(8\\) 都影响不到 \\(4\\) 的颜色。
　　所以设 \\(dp(i,0/1)\\) 表示涂完前 \\(i\\) 个数的方案数，那么 \\(7,8,9,11\\) 这些数单独组成一个影响连通块，这一块对 \\(7\\) 以前的数的颜色没有任何影响，可以有 \\(dp(6)+=dp(2)\\)。

　　现在我们要预处理出每个数最多往前影响多少位。
　　设 \\(pos(i,0/1)\\) 表示第 \\(i\\) 个数涂红/蓝色，它往前最近的影响不到的数在哪一位。
　　则 \\(pos\\) 可以递推，比如上例中，\\(pos(6,0)=pos(4,1)=pos(3,0)=2\\)。
　　于是用 \\(dp\\) 的递推式 \\(dp(i)=dp(pos(i,0/1))\\) 推出 \\(dp(n)\\) 即可。

　　当然，这个做法需要特判无解的情况。
　　比如上例中 \\(11\\) 涂成红色，\\(8,9\\) 就必须涂成蓝色，但 \\(8,9\\) 两个数差 \\(1\\)，\\(B=4\\)，所以不能同时涂成蓝色。这时 \\(pos(6,0)=-1\\)。最后计算 \\(dp(i)\\) 时跳过 \\(pos(i,j)=-1\\) 的情况。
　　我们需要用 \\(\\textST\\) 表、线段树等数据结构维护区间最小差分值。
　　复杂度 \\(O(n\\log n)\\)。

　　code

solution 3