每日一题_190914

Posted 2022-10-28 math521

在 \\(\\triangle ABC\\) 中, \\(\\sin \\dfrac\\angle ABC2=\\dfrac\\sqrt33\\), 点 \\(D\\) 在线段 \\(AC\\) 上, 且 \\(AD=2DC\\), \\(BD=\\dfrac4\\sqrt33\\), 则 \\(\\triangle ABC\\) 的面积的最大值为\\(\\underline\\qquad\\qquad\\).
解析:
法一 根据题意有
\\[ \\cos\\angle ABC=1-2\\sin^2\\dfrac\\angle ABC2=\\dfrac 13.\\]
因此 \\(\\angle ABC\\) 是一个大小确定的锐角, 并且 \\(\\tan\\angle ABC = 2\\sqrt 2\\). 如图, 建立平面直角坐标系.

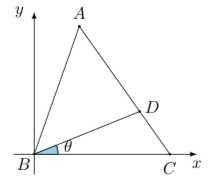
设 \\(\\theta=\\angle DBC, C(x,0)\\). 则 \\(D\\) 点坐标为\\[ \\begincases & x_D=BD\\cdot \\cos\\theta=\\dfrac4\\sqrt33\\cos\\theta,\\ & y_D=BD\\cdot \\sin\\theta=\\dfrac4\\sqrt33\\sin\\theta. \\endcases\\] 又 \\(D\\) 点是线段 \\(AC\\) 上靠近 \\(C\\) 点的三等分点, 从而 \\(A\\) 点坐标易求得\\[ \\left( x_A,y_A\\right)=\\left( 4\\sqrt3\\cos\\theta-2x,4\\sqrt3\\sin\\theta \\right).\\]
结合 \\(k_AB=\\tan\\angle ABC=2\\sqrt2\\) 可得 \\(x,\\theta\\) 的关系式如下\\[ \\dfrac4\\sqrt3\\sin\\theta4\\sqrt3\\cos\\theta-2x=2\\sqrt2.\\]
即有 \\(x=2\\sqrt3\\cos\\theta-\\dfrac\\sqrt62\\sin\\theta\\). 从而 \\(\\triangle ABC\\) 的面积\\[ \\beginsplit S_\\triangle ABC&=3S_\\triangle DBC=3\\cdot \\dfrac 12\\cdot BD\\sin\\theta\\cdot BC\\ &=3\\cdot \\dfrac 12\\cdot \\dfrac4\\sqrt33 \\sin\\theta\\cdot \\left( 2\\sqrt3\\cos\\theta-\\dfrac\\sqrt62\\sin\\theta\\right) \\ &=6\\cdot \\left( \\sin 2\\theta+\\dfrac\\sqrt24\\cos 2\\theta-\\dfrac\\sqrt24 \\right)\\ &\\leqslant 3\\sqrt2. \\endsplit\\]
当且仅当 \\(\\tan 2\\theta=2\\sqrt2\\), 也即 \\(\\tan\\theta =\\dfrac\\sqrt 22\\) 时, 上述不等式取等, 因此所求三角形面积最大值为 \\(3\\sqrt 2\\).
法二 如图, 作辅助线 \\(CE\\), 使得 \\(CE\\parallel AB\\), 延长 \\(BD\\) 交 \\(CE\\) 于点 \\(E\\),

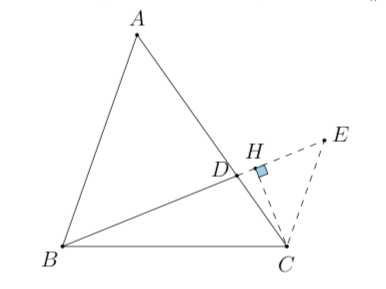
则 \\(\\triangle ABD\\sim \\triangle CED\\), 且相似比为 \\(2:1\\), 于是
\\[ BE=BD+DE=BD+\\dfrac12 BD=2\\sqrt3. \\]并且\\[ \\angle BCE=\\angle BCD+\\angle ECD=\\angle BCA+\\angle BAC=\\pi-\\angle ABC.\\] 故 \\(\\triangle BCE\\) 中存在定弦定角模型, 作 \\(CH\\perp BE\\), 垂足为 \\(H\\), 显然当 \\(H\\) 为 \\(BE\\) 中点时 \\(CH\\) 取得最大值. 即
\\[ \\beginsplit S_\\triangle ABC&=3S_\\triangle DBC=2S_\\triangle EBC\\ &=2\\cdot \\dfrac 12\\cdot CH\\cdot BE\\ &\\leqslant \\left( \\dfrac 12BE \\cdot \\tan \\dfrac\\angle ABC2\\right)\\cdot BE\\ &=3\\sqrt 2. \\endsplit \\] 因此所求三角形面积最大值为 \\(3\\sqrt2\\).