51nod1730 涂边

Posted 2022-10-27 gmh77

题目描述

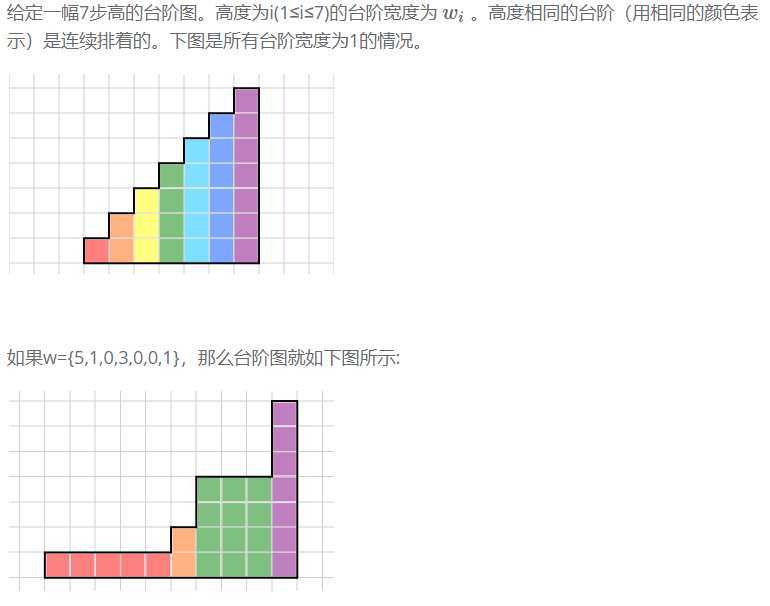
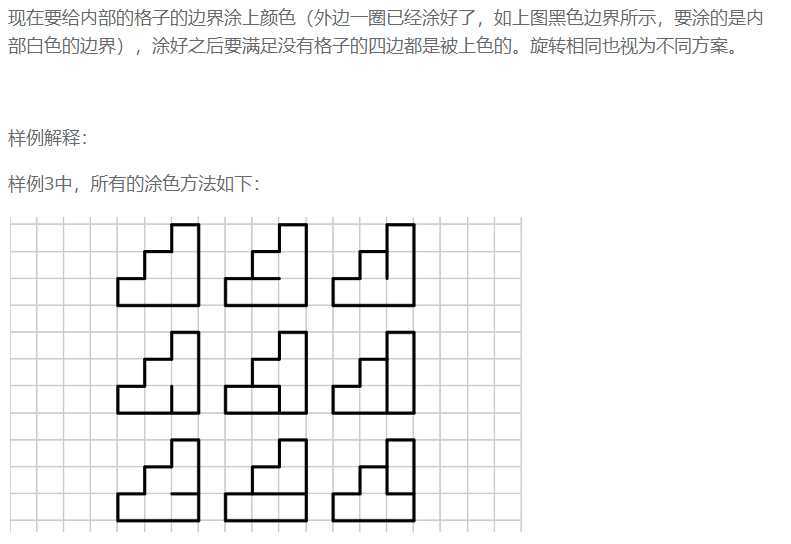
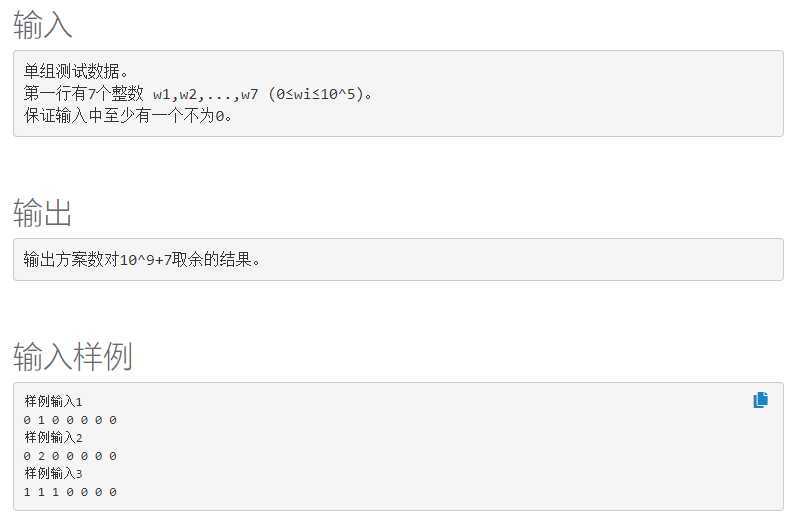
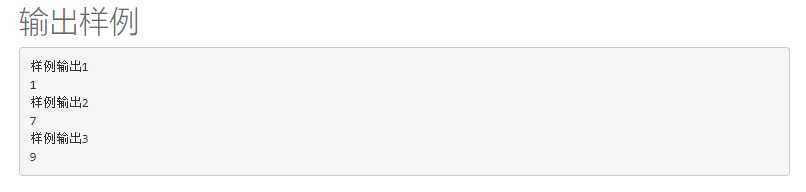
题解

八级sb题

显然可以想到状压

枚举当前的宽度\\(I\\)，设\\(f[s]\\)表示在当前的宽度下选的竖边的状态为s

再设\\(g[s1][s2]\\)表示状态s1转移到s2的方案数，枚举中间横边的集合s3

显然一个合法的方案中不能存在四边都是边的方格，即\\(s1\\&s2\\&(s3+2^I-1)\\&((s3<<1)+1)\\)

如果第i个格子存在四边，那么只能是\\(s1\\)的第\\(i-1\\)位（即\\(2^i-1\\)）、\\(s2\\)的第\\(i-1\\)位、\\(s3\\)的第\\(i-2\\)位和第\\(i-1\\)位都存在，于是就有了上面的式子

dp随便转移，然而这样会挂（

矩乘加速即可

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 1000000007
using namespace std;

int p[8]=0,1,2,4,8,16,32,64;
int w[8];
long long f[2][128];
long long a[128][128];
long long b[128][128];
long long c[128][128];
int i,j,k,l,I,L,i2,i3;

int main()

//  freopen("51nod1730.in","r",stdin);
//  freopen("51nod1730.out","w",stdout);
    
    fo(i,1,7)
    scanf("%d",&w[i]);
    
    i2=0;
    f[0][0]=1;
    
    fo(I,1,7)
    
        i3=i2^1;
        memset(f[i3],0,sizeof(f[i3]));
        
        L=p[I]*2-1;
        fo(i,0,p[I]-1)
        f[i3][i|p[I]]=f[i2][i];
        i2=i3;
        
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        fo(i,0,L)
        
            fo(j,0,L)
            
                fo(k,0,p[I]-1)
                if (!(i&j&((k<<1)+1)&(k+p[I])))
                ++b[i][j];
            
        
        fo(i,0,L)
        a[i][i]=1;
        
        while (w[I])
        
            if (w[I]&1)
            
                memset(c,0,sizeof(c));
                fo(i,0,L)
                
                    fo(j,0,L)
                    
                        fo(k,0,L)
                        c[i][j]=(c[i][j]+a[i][k]*b[k][j])%mod;
                    
                
                fo(i,0,L)
                
                    fo(j,0,L)
                    a[i][j]=c[i][j];
                
            
            
            memset(c,0,sizeof(c));
            fo(i,0,L)
            
                fo(j,0,L)
                
                    fo(k,0,L)
                    c[i][j]=(c[i][j]+b[i][k]*b[k][j])%mod;
                
            
            fo(i,0,L)
            
                fo(j,0,L)
                b[i][j]=c[i][j];
            
            
            w[I]>>=1;
        
        
        i3=i2^1;
        memset(f[i3],0,sizeof(f[i3]));
        
        fo(j,0,L)
        
            fo(k,0,L)
            f[i3][j]=(f[i3][j]+f[i2][k]*a[k][j])%mod;
        
        i2=i3;
    
    
    printf("%lld\\n",f[i2][p[7]*2-1]);
    
    fclose(stdin);
    fclose(stdout);
    
    return 0;