几何的简单操作

Posted 2022-10-11 tingtin

点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影，有公式：

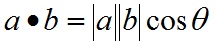
    a·b>0    方向基本相同，夹角在0°到90°之间

     a·b=0    正交，相互垂直  

     a·b<0    方向基本相反，夹角在90°到180°之间 

 

对于向量a和向量b：

                                                

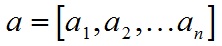
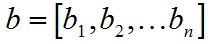
a和b的点积公式为：

 

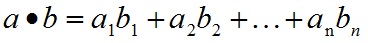
//矩阵乘法
#include <bits/stdc++.h>
using namespace std;
#define N 100
int a[N][N],b[N][N],c[N][N];
int main()

    int m,s,n;
    scanf("%d%d%d",&m,&s,&n);
    for(int i =1;i<=n;i++)
        for(int j =1;j<=s;j++)
            scanf("%d",&a[i][j]);
        
    
    for(int i =1;i<=s;i++)
        for(int j =1;j<=n;j++)
            scanf("%d",&b[i][j]);
        
    
    for(int i=1;i<=m;i++)
        for(int j =1;j<=n;j++)
            for(int k =1;k<=s;k++)
                c[i][j]+=a[i][k]*b[k][j];
            
        
    
    for(int i =1;i<=m;i++)
        for(int j=1;j<=n;j++)
            printf("%d ",c[i][j]);
        
        printf("\\n");
    
    return 0;

 

 

行列式N行N列

 

 

 

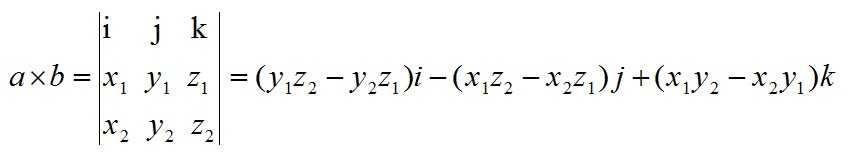
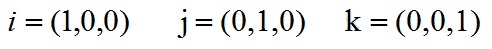
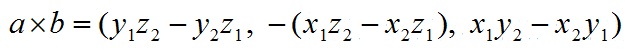
叉乘的几何意义：

在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面。

在3D图像学中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。

在二维空间中，叉乘还有另外一个几何意义就是：aXb等于由向量a和向量b构成的平行四边形的面积。