逻辑回归-4.添加多项式特征

Posted 2022-10-07 shuai-long

逻辑回归解决二分类问题，但是像下图所示的非线性数据集，是没办法用一条直线分割为两部分的。

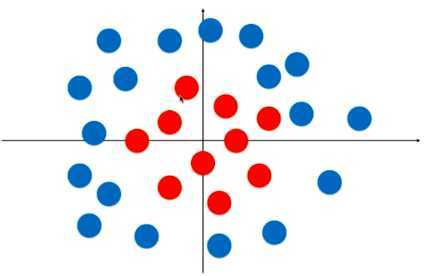
对于此数据集，用一个圆形或者椭圆形分割是比较合理的，圆形的表达式：\\(X_1^2 + X_2^2 - R^2 = 0\\)
为了让逻辑回归学习到这样的决策边界，我们需要引入多项式项，\\(X_1^2,X_2^2\\)分别是\\(X_1,X_2\\)的二次多项式。使用多项式后，可以定义任意圆心位置的圆、椭圆或不规则形状的决策边界。

代码实现

构造数据集

import numpy
import matplotlib.pyplot as plt

numpy.random.seed(666)
X = numpy.random.normal(0,1,size=(200,2))
y = numpy.array(X[:,0]**2 + X[:,1]**2 < 1.5,dtype='int')

plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()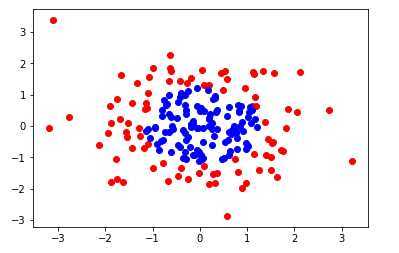

逻辑回归算法测试

from mylib.LogisticRegression import LogisticRegression

log = LogisticRegression()
log.fit(X,y)

算法正确率只有60%

画出决策边界：

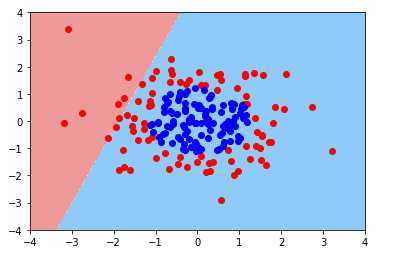
可以看出，用线性分类来拟合此数据集是错误的

添加多项式，并使用管道

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

def PolynomialLogisticRegression(degree):
    return Pipeline([
        ('poly',PolynomialFeatures(degree=degree)),
        ('stand_scalor',StandardScaler()),
        ('log_reg',LogisticRegression())
    ])

poly_log_reg = PolynomialLogisticRegression(2)
poly_log_reg.fit(X,y)

注意：管道中的逻辑回归是自己实现的，但是能准确的传递到管道中，这是因为我们是仿照scikit-learn的标准实现的

添加多项式后，算法的准确率提高到了95%

决策边界：

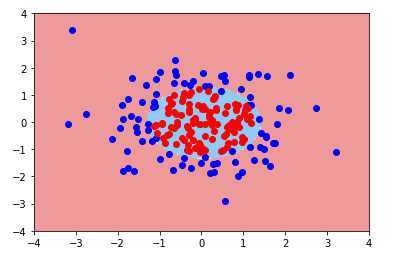
当多项式项为20时

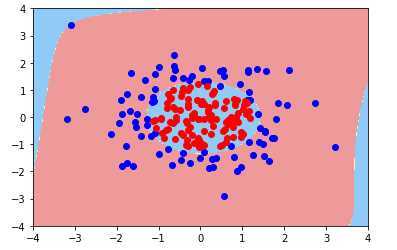
随着项数的增加，算法变得复杂，趋于过拟合，但为了得到复杂形状的决策边界，又不能过多的减小多项式项，此时，应该考虑模型的正则化，见下章。