最小生成树

Posted 2022-09-26 xcxfury001blogs

一、概念

在一个连通图的所有生成树中，各边的代价之和最小的那棵生成树称为该连通网的最小代价生成树，简称最小生成树。

二、构建最小生成树的方法

1.普利姆算法

首先，我们假设有一棵只包含一个顶点v（v可为图中的任意一点）的树T。然后贪心地选取T和其他顶点之间相连的最小权值的边，并把它加到T中。

不断进行这个操作，就可以得到一棵生成树了。

以此图为例

 

 

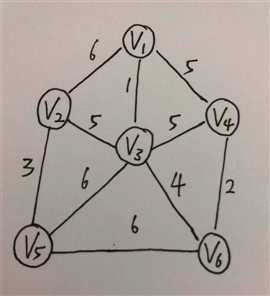
 初始先将V1（随便一个都可以，这里以V1举例）加入到最小生成树，则得到信息表为如下：

 

 

 最小生成树中只有V1一个点，最小生成树到各点的距离如图所示。下一步添加最小的边，因为v1已经在最小生成树中，所以添加v3。

更新此表。

 

 

 

 

 

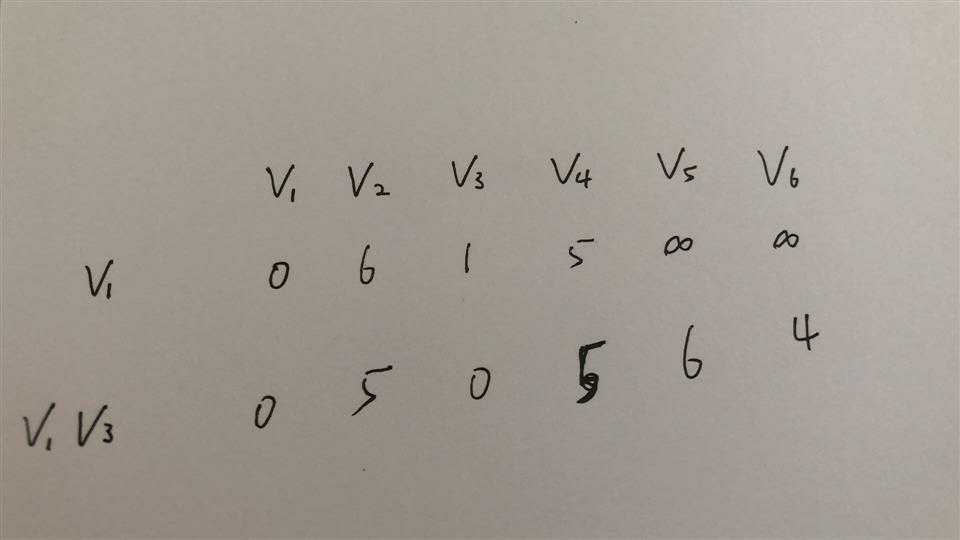
则此时最小权值为4，添加v6。以此类推，添加所有的点到最小生成树。

代码：

int cost[maxv][maxv];//cost[u][v]表示边e=(u,v)的权值（不存在的情况为inf），
int mincost[maxv];//从最小生成树出发的边到每个顶点的最小权重
bool used[maxv];//顶点i是否包含在最小生成树中
int V;//顶点数
int prim()

    for(int i=0;i<V;i++)
    
        mincost[i] = inf;//inf的值是比最大权值边的值还要大的一个数
        used[i] = false;
    
    mincost[0] = 0;//先添加的是第0个点
    int res = 0;//最小生成树的最小权值
    while(true)
    
        int v = -1;
        //从不属于X的顶点中选取从X到其权值最小的顶点。X为最小生成树的集合
        for(int u = 0;u<V;u++)
        
            if(!used[u] && (v==-1 || mincost[u]<mincost[v])) v = u;
        
        if(v==-1)
        
            break;
        
        used[v] = true;//把顶点v加入到X中
        res += mincost[v];//把边的长度加到结果里
        //更新mincost
        for(int u=0;u<V;u++)
        
            mincost[u] = min(mincost[u],cost[v][u]);
        
    

时间复杂度O(n²).

 2.Kruskal算法

按照边的权值顺序从小到大查看一遍，如果不产生圈（重边等也算在内），就把当前这条边加入到生成树中。

难点：如何判断是否产生圈。假设现在要把顶点u和顶点v的边e加入到生成树中。如果加入之前u和v不在同一个连通分量

里，则加入e也不会产生圈。反之，如果u和v在同一个连通分量里，那么一定会产生圈。

可以使用并查集高效的判断是否属于同一个连通分量。

插入一段关于并查集的介绍：

并查集是什么？

并查集是一种用来管理元素分组情况的数据结构。可以高效的进行如下操作

1）查询元素a和元素b是否属于同一个组。

2）合并元素a和元素b所在的组。

并查集的实现

int par[maxn];//父亲
int rank[maxn];//树的高度
//初始化n个元素
void init(int n)

    for(int i=0;i<n;i++)
    
        par[i] = i;//每个节点都是一棵树
        rank[i] = 0;
    

//查询树的根
int find(int x)

    if(par[x]==x)
    
        return x;
    else
    
        return par[x] = find(par[x]);
    


//合并x和y所属的集合
void unite(int x,int y)

    x = find(x);
    y = find(y);
    //x和y属于同一个集合
    if(x==y) return;

    if(rank[x]<rank[y])
    
        par[x] = y;
    else
    
        par[y] = x;
        if(rank[x]==rank[y]) rank[x]++;
    

//判断x和y是否属于同一个集合
bool same(int x,int y)

    return find(x)==find(y);

Kruskal算法代码：

struct edge

    int u,v,cost;
;
bool comp(const edge e1,const edge e2)

    return e1.cost<e2.cost;

edge es[maxe];
int V,E;//顶点数和边数

int kruskal()

    sort(es,es+E,comp);
    init(V);//初始化并查集
    int res = 0;
    for(int i=0;i<E;i++)
    
        edge e = es[i];
        if(!same(e.u,e.v))
        
            unite(e.u,e.v);
            res += e.cost;
        
    
    return res;

时间复杂度O(|E|log|E|)。