左神算法书籍《程序员代码面试指南》——3_02打印二叉树的边界节点★★

Posted 2022-09-24 zzw1024

【题目】
给定一棵二叉树的头节点head，按照如下两种标准分别实现二叉树边界节点的逆时针打印。
标准一：
1.头节点为边界节点。
2.叶节点为边界节点。
3.如果节点在其所在的层中是最左或最右的，那么也是边界革点。
标准二：
1.头节点为边界节点。
2.叶节点为边界节点。
3.树左边界延伸下去的路径为边界节点。
4.树右边界延伸下去的路径为边界节点。
例如，如图3 - 2所示的树。

 

 

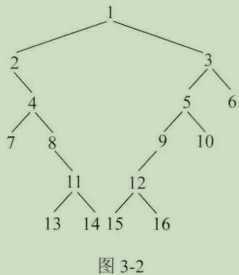
按标准一的打印结果为：1，2，4，7，11，13，14，15，16，12，10，6，3
按标准二的打印结果为：1，2，4，7，13，14，15，16，10，6，3
【要求】
1.如果节点数为N，两种标准实现的时间复杂度要求都为O(N)，额外空间复杂度要求都为O(h)，h为二叉树的高度。
2.两种标准都要求逆时针顺序且不重复打印所有的边界节点。
【解答】
按照标准一的要求实现打印的具体过程如下：
1.得到二叉树每一层上最左和最右的节点。以题目的例子来说，这个记录如下：
最左节点 最右节点
第一层 1 1
第二层 2 3
第三层 4 6
第四层 7 10
第五层 11 12
第六层 13 16
2.从上到下打印所有层中的最左节点。对题目的例子来说，即打印：1，2，4，7，11，13。
3.先序遍历二叉树，打印那些不属于某一层最左或最右的节点，但同时又是叶节点的节点。对题目的例子来说，即打印：14，15。
4.从下到上打印所有层中的最右节点，但节点不能既是最左节点，又是最右节点。对题目的例子来说，即打印：16，12，10，6，3。
////////////标准一/////////////////

 1 int getHeight(Node* h, int l)//获取二叉树层数
 2 
 3 if (h == nullptr)
 4 return l;
 5 return max(getHeight(h->l, l + 1), getHeight(h->r, l + 1));
 6 
 7 void setEdgeMap(Node* h, int l, vector<vector<Node*>>&edgeMap)
 8 
 9 if (h == nullptr)
10 return;
11 edgeMap[l][0] = edgeMap[l][0] == nullptr ? h : edgeMap[l][0];
12 edgeMap[l][1] = h;
13 setEdgeMap(h->l, l + 1, edgeMap);//向左找左边界
14 setEdgeMap(h->r, l + 1, edgeMap);//向右找右边界
15 
16 void printLeafEdge(Node* h, int l, vector<vector<Node*>>edgeMap)
17 
18 if (h == nullptr)
19 return;
20 if (h->l == nullptr && h->r == nullptr && h != edgeMap[l][0] && h != edgeMap[l][1])//是叶子节点，但不是左右边界节点
21 cout << h->v << " ";
22 printLeafEdge(h->l, l + 1, edgeMap);//向下寻找该边界叶子节点
23 printLeafEdge(h->r, l + 1, edgeMap);
24 
25 void printEdge1(Node* root)
26 
27 if (root == nullptr)
28 return;
29 int h = getHeight(root, 0);//得到深度
30 vector<vector<Node*>>edgeMap(h, vector<Node*>(2));//每一层的左右边界
31 setEdgeMap(root, 0, edgeMap);
32 //先打印左边界
33 for (int i = 0; i < edgeMap.size(); ++i)
34 cout << edgeMap[i][0]->v << " ";
35 //打印不是左右边界，但是节点边界的节点
36 printLeafEdge(root, 0, edgeMap);
37 //打印右边界节点
38 for (int i = edgeMap.size() - 1; i >= 0; --i)
39 if (edgeMap[i][0] != edgeMap[i][1])
40 cout << edgeMap[i][1]->v << " ";
41 

 

按照标准二的要求实现打印的具体过程如下：
1.从头节点开始往下寻找，只要找到第一个既有左孩子，又有右孩子的节点，记为h，则进入步骤2。在这个过程中，找过的节点都打印。对题目的例子来说，即打印：1，因为头节点直接符合要求，所以打印后没有后续的寻找过程，直接进入步骤2。但如果二叉树如图3 - 3所示，此时则打印：1，2，3。节点3是从头节点开始往下第一个符合要求的。如果二叉树从上到下一直找到叶节点也不存在符合要求的节点，说明二叉树是棒状结构，那么打印找过的节点后直接返回即可。
2.h的左子树先进入步骤3的打印过程；h的右子树再进入步骤4的打印过程；最后返回。
3.打印左边界的延伸路径以及h左子树上所有的叶节点，具体请参看printLeftEdge方法。
4.打印右边界的延伸路径以及h右子树上所有的叶节点，具体请参看printRightEdge方法。
////////////标准二/////////////////

 1 void printLeftEdge(Node* h, bool f)
 2 
 3 if (h == nullptr)
 4 return;
 5 if (f || (h->l == nullptr && h->r == nullptr))//边界叶子节点
 6 cout << h->v << " ";
 7 printLeftEdge(h->l, f);
 8 printLeftEdge(h->r, f && h->l == nullptr ? true : false);
 9 
10 void printRightEdge(Node* h, bool f)
11 
12 if (h == nullptr)
13 return;
14 printLeftEdge(h->l, f && h->r == nullptr ? true : false);
15 printLeftEdge(h->r, f);
16 if (f || (h->l == nullptr && h->r == nullptr))//边界叶子节点
17 cout << h->v << " ";
18 
19 void printEdge2(Node* root)
20 
21 if (root == nullptr)
22 return;
23 cout << root->v << " ";//根节点满足要求
24 if (root->l != nullptr && root->r != nullptr)
25 
26 printLeftEdge(root->l, true);
27 printRightEdge(root->r, true);
28 
29 else
30 printEdge2(root->l != nullptr ? root->l : root->r);
31 
32