归并排序+归并排序求逆序对（例题P1908）

Posted 2020-11-12 winter-bamboo

归并排序（merge sort)

顾名思义，这是一种排序算法，时间复杂度为O(nlogn)，时间复杂度上和快排一样

归并排序是分治思想的应用，我们先将n个数不断地二分，最后得到n个长度为1的区间，显然，这n个小区间都是单调的，随后合并相邻的两个区间，得到n/2个单增（减）的区间，随后我们继续合并相邻的两个区间，得到n/4个单增（减）的区间....

每次合并操作的总时间复杂度为O(n)，logn次合并用时O(logn)，故总时间复杂度为O(nlogn)

合并操作比较好理解，就像下图这样二分区间即可（红线代表分割线）：

 

然后，我们要如何实现O(n)的复杂度实现区间合并呢？

我们另开一个大小和原数组a大小一样的数组alt，存储需要合并的两个区间的数，方便起见，我们用pos代表alt数组的当前指向的位置，用i表示左区间当前所指的位置，用j表示右区间当前所指的位置，如下图所示：

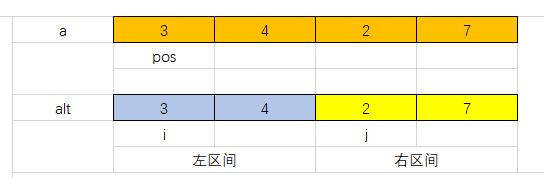
记此时我们合并形成的区间为[l,r]，按升序排序，那么我们枚举这一区间中的pos，每次比较alt[i]和alt[j]，如果alt[i] < alt[j] 那么令a[pos] = alt[i]，同时pos++,i++ ，否则令a[pos] = alt[j] ，同时pos++,j++，如果左区间的数已经全部遍历，那么将右区间剩下的数依次加入pos位置，反之同理，操作过程如下图所示：

  

    

  

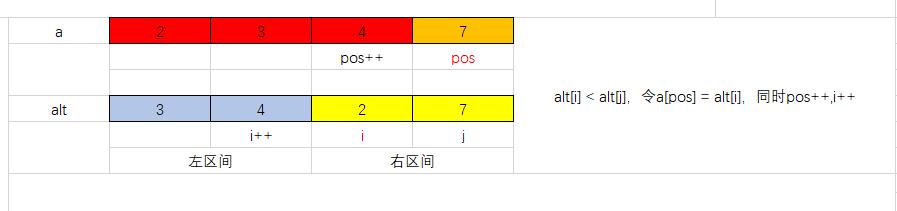
至此，区间[l,r]这一段区间已经完成排序，这就是归并排序的合并过程

归并排序代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>

#define bug cout << "**********" << endl
#define show(x, y) cout<<"["<<x<<","<<y<<"] "
#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 1e9 + 7;
const ll mod = 1e9 + 7;
const int Max = 5e5 + 10;

int n;
ll sum;
int alt[Max];

void merge(int a[], int l, int r)
{
    for(int i= l; i <= r; i ++)
    {
        alt[i] = a[i];
    }
    int mid = (l + r) >> 1;
    int i = l, j = mid + 1;
    for (int pos = l; pos <= r; pos++)
    {
        if (i == mid + 1)
        {
            a[pos] = alt[j];
            j++;
        }
        else if (j == r + 1)
        {
            a[pos] = alt[i];
            i++;
        }
        else if (alt[i] > alt[j])
        {
            a[pos] = alt[j];
            j++;
        }
        else
        {
            a[pos] = alt[i];
            i++;
        }
    }
}

void merge_sort(int a[], int l, int r)
{
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    merge_sort(a, l, mid);
    merge_sort(a, mid + 1, r);
    merge(a, l, r);
}


int a[Max];

int main()
{
#ifdef LOCAL
    //    freopen("input.txt", "r", stdin);
    //    freopen("output.txt", "w", stdout);
#endif
    sum = 0;
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", a + i);
    merge_sort(a, 0, n - 1);
    for(int i = 0 ;i < n ;i ++)
        printf("%d%c",a[i],i == n-1?\'\\n\':\' \');
    return 0;
}

View Code

利用归并排序求逆序对

我们注意到在归并排序过程中，我们有一步判断：if(alt[i] > alt[j]) ,如果判断为真，那么显然，j 和 区间[i,mid]每一个点都形成逆序对，一共mid-i+1个，而且只在这个地方会出现形成逆序对的情况，那么情况就很简单了，我们将原数组进行归并排序，并在if(alt[i] > alt[j] ) 为真的时候，统计一下逆序对的个数即可。

代码区

(点击此处查看模板题）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>

#define bug cout << "**********" << endl
#define show(x, y) cout<<"["<<x<<","<<y<<"] "
#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 1e9 + 7;
const ll mod = 1e9 + 7;
const int Max = 5e5 + 10;

int n;
ll sum;
int alt[Max];

void merge(int a[], int l, int r)
{
    for(int i= l; i <= r; i ++)
    {
        alt[i] = a[i];
    }
    int mid = (l + r) >> 1;
    int i = l, j = mid + 1;
    for (int pos = l; pos <= r; pos++)
    {
        if (i == mid + 1)
        {
            a[pos] = alt[j];
            j++;
        }
        else if (j == r + 1)
        {
            a[pos] = alt[i];
            i++;
        }
        else if (alt[i] > alt[j])
        {
            a[pos] = alt[j];
            j++;
            sum += mid - i + 1;        //i及其此后的都可以和a[j]形成逆序对
        }
        else
        {
            a[pos] = alt[i];
            i++;
        }
    }
}

void merge_sort(int a[], int l, int r)
{
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    merge_sort(a, l, mid);
    merge_sort(a, mid + 1, r);
    merge(a, l, r);
}


int a[Max];

int main()
{
#ifdef LOCAL
    //    freopen("input.txt", "r", stdin);
    //    freopen("output.txt", "w", stdout);
#endif
    sum = 0;
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", a + i);
    merge_sort(a, 0, n - 1);
    printf("%lld\\n", sum);
    return 0;
}

View Code