poj3471 - 倍增+LCA+树上差分

Posted 2022-09-24 lesning

题意：一张n节点连通无向图，n-1条树边，m条非树边。若通过先删一条树边，再删一条非树边想操作   

将此图划分为不连通的两部分，问有多少种方案。

 

 

 

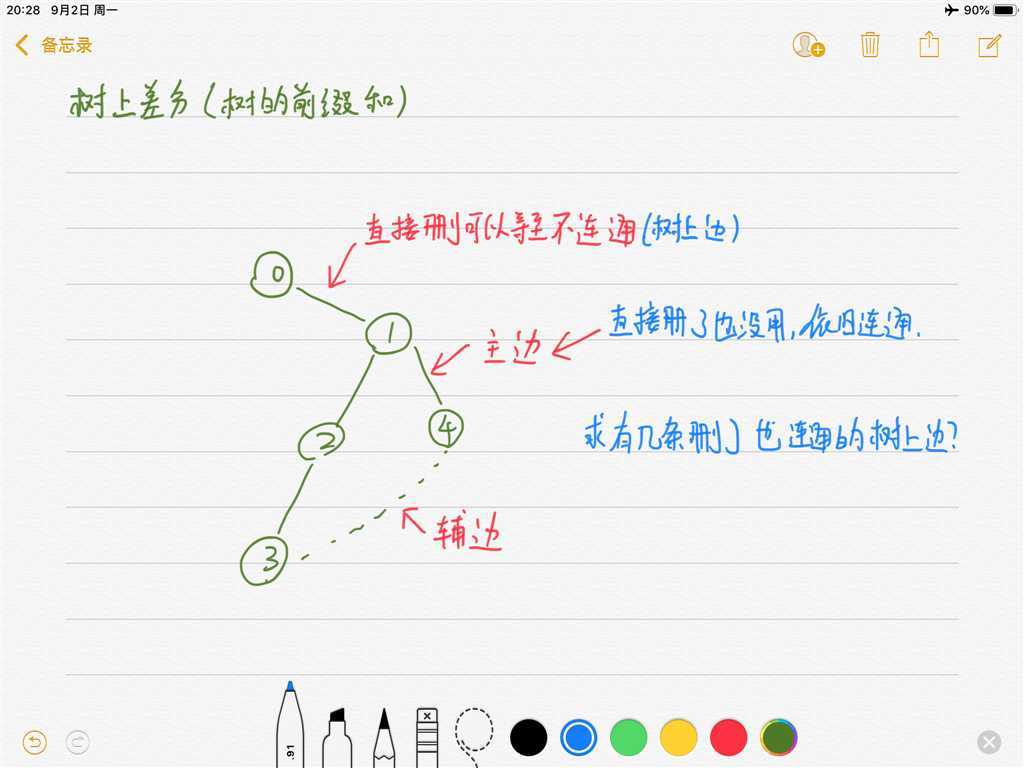
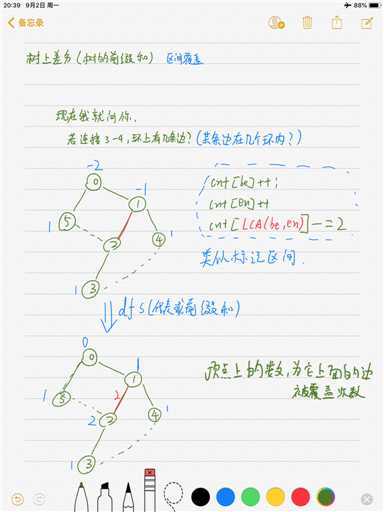
 利用LCA整好区间覆盖，dfs用来求前缀和

需要注意的是，覆盖数为1的时候才可以选择哦！

覆盖数为0，代表可以直接拆开

 

最后附上一张我老婆

 

 

 

 

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#define maxn 110000
using namespace std;
typedef long long ll;
int dp[maxn][33];
int dep[maxn];
long long cnt[maxn];//差分数组
int head[450100];

struct Node 
	int to;
	int next;
G[450100];
int cnn = 1;
void insert(int be, int en) 
	G[cnn].to = en; G[cnn].next = head[be]; head[be] = cnn;;//头插法
	cnn++;


void dfs(int u, int par) 
	dep[u] = dep[par] + 1;
	for (int i = 0; i <= 21; i++) 
		dp[u][i + 1] = dp[dp[u][i]][i];
	
	for (int i = head[u]; i; i = G[i].next) 
		int p = G[i].to;
		if (p == par) continue;
		dp[p][0] = u;
		dfs(p, u);
	
	return;

int LCA(int x, int y) 
	if (dep[x] < dep[y]) swap(x, y);//x在下面
	for (int i = 20; i >= 0; i--) 
		if (dep[dp[x][i]]  >= dep[y]) x = dp[x][i];
		if (x == y) return x;
	
	
	for (int i = 20; i >= 0; i--) 
		if (dp[x][i] != dp[y][i]) 
			x = dp[x][i];
			y = dp[y][i];
		
		
	
	
	return dp[x][0];

int n, m;
int find(int x,int par) 
	
	for (int i = head[x]; i; i = G[i].next) 
		int p = G[i].to;
		if (p == par) continue;
		find(p, x);
		cnt[x] += cnt[p];
	
	
	return 0;

int main() 
	scanf("%d %d", &n, &m);
	int be, en;
	for (int i = 0; i < n - 1; i++) 
		scanf("%d %d", &be, &en);
		insert(be, en);
		insert(en, be);
	
	dp[1][0] = 1;
	dfs(1, 0);
	for(int i=0;i<m;i++) 
		scanf("%d %d", &be, &en);
		int p = LCA(be, en);
		cnt[p] -= 2;
		cnt[be]++;
		cnt[en]++;
	
	find(1, 0);
	ll ans = 0;
	
	for (int i = 2; i <= n; i++) 
		if (cnt[i] == 0) ans += m;//乘法原理
		else if (cnt[i] == 1) ans++;
	
	printf("%lld\\n", ans);
	return 0;