图片：空域分析及变换

Posted 2022-09-21 tadeas

滤波/卷积函数
\\[h[x,y]=\\sum\\limits_k,lf[k,l]I[x+k,y+l]\\]
其中，\\(I\\)表示对应的像素点，\\(f(x,y)\\)为滤波函数，\\(k, l\\)为扫扫描窗（卷积核）中的任意点。
在卷积的过程中，需要注意的是padding, 根据padding的类型可以大致分为：zero-padding, replication(边界复制), reflection(镜像)和wraparound(块复制)

根据功能的不同，函数\\(f(x,y)\\)的功能也不尽相同。

图像增强：

1.平滑/去噪
滤波器的参数和为1，且核的尺寸为奇数\\((2n-1)\\cdot(2n-1)\\)
常见的滤波器：

*平滑均值滤波/卷积，一般 \\(3\\cdot3\\), step =1, zero-padding

*平滑中值滤波/卷积，一般\\((2n-1)\\cdot(2n-1)\\), step =1, 卷积核内的像素从小到大排序取中值作为卷积的输出，该算法可以有效的去除椒盐噪声

*平滑高斯滤波/卷积，一般\\((2n-1)\\cdot(2n-1)\\), 模拟人眼，关注中心区域，有效的去除高斯噪声
e.g.:
\\[G_\\sigma =\\frac12\\pi \\sigma ^2e^-\\fracx^2+y^22\\sigma ^2\\]

0.003	0.013	0.022	0.013	0.003
0.013	0.059	0.097	0.059	0.013
0.022	0.097	0.159	0.097	0.022
0.013	0.059	0.097	0.059	0.013
0.003	0.013	0.022	0.013	0.003

其中，\\(\\sigma\\) 越小，关注区域越集中；相反，\\(\\sigma\\) 越大，关注区域越分散。

$ $
左图\\(\\sigma=1\\)，右图\\(\\sigma=4\\)

对于平滑高斯滤波器具有很好的对称性，可以拆分为级联的高斯，如2D的卷积，可拆分为两个相同的1D的卷积，即：
\\[G_\\sigma =\\frac12\\pi \\sigma ^2e^-\\fracx^2+y^22\\sigma ^2=\\frac1\\sqrt2\\pi \\sigma e^-\\fracx^22\\sigma ^2\\frac1\\sqrt2\\pi \\sigma e^-\\fracy^22\\sigma ^2\\]

$ $
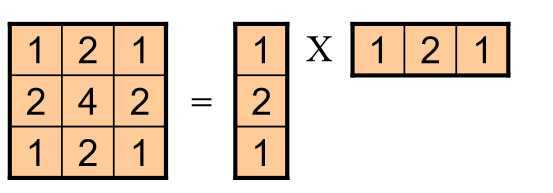
2D高斯转换为两个1D高斯核乘积

2.梯度/锐化

信息提取、检测; 边缘、显著点、纹理;模式

*梯度Prewitt滤波/卷积
1.水平梯度/垂直边缘

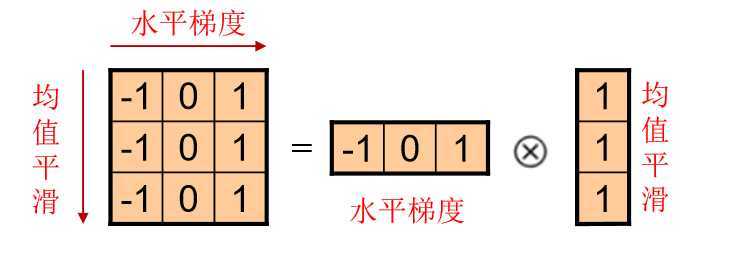
2.垂直梯度/水平边缘

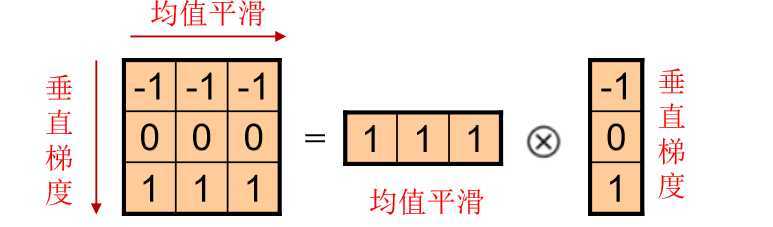
*梯度Sobel滤波/卷积
1.水平梯度/垂直边缘

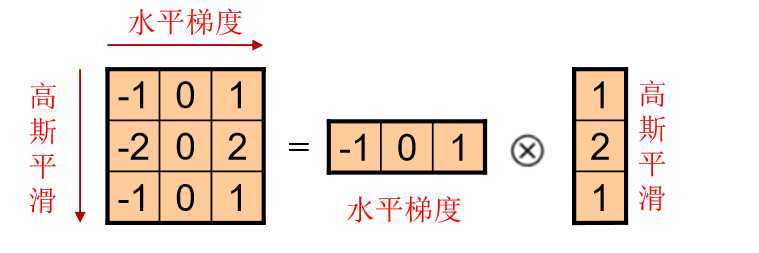
2.垂直梯度/水平边缘

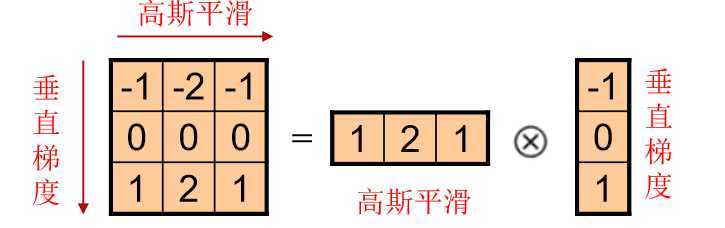
*梯度Laplacian滤波/卷积

\\[\\Delta f=\\frac\\partial ^2f\\partial x^2+\\frac\\partial ^2f\\partial y^2\\]
可用于团块检测和边缘检测