排序问题之归并排序

Posted 2022-09-19 lzamonologue

最近在看算法导论，一开始就讲了许多关于各种排序的问题，（原谅我之前只会STL模板库里的sort函数），正好oj上有一个简单排序题，如图：

 题意就是将序列排序然后找第k个数就行了，先随便交一发过了之后我觉得我应该学一些别的算法，于是这两天看懂了归并算法然后进行了实现。

归并排序

其实质就是分治，首先考虑下如何将左右两个有序数列合并。这个非常简单，只要从比较这两个数列的第一个数，谁小就先将他放入要排序的数列中。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可。

这个排序其实非常简单，让我们从小规模来看，当一个数组只有一个数的时候，显然他是有序的，当有两个数的时候，把这两个数分成两组，这两组各自都是有序的，然后将其合并，以此类推，通过不断地递归和合并，我们就能实现排序的目的了

合并的过程：

void merge(int arr[],int l,int mid,int r)   //我们将整个数组分为左部和右部，l为左部数组的起始点，mid作为两个数组的分割点，r为右部数组的结尾点，即两个数组分别为L[l....mid],R[mid+1.....r]，这两个数组都是有序的


    int llen=mid-l+1,rlen=r-mid;     //两个数组的长度
    int x[llen],y[rlen];             //新开辟两个的数组用来存放未排序的数据
    for(int i=0;i<llen;i++)
    
        x[i]=arr[l+i];
    
    for(int i=0;i<rlen;i++)
    
        y[i]=arr[mid+1+i];
    
    int j=0,k=0;
    for(int i=l;i<=r;i++)
    
        if(x[j]<=y[k]&&j<llen&&k<rlen)       //谁小谁在前
        
            arr[i]=x[j++];
        
        else if(x[j]>y[k]&&j<llen&&k<rlen)
        
            arr[i]=y[k++];
        
        else if(j>=llen)           //谁先放完另一个数组接着依次放入
        
            arr[i]=y[k++];
        
        else if(k>=rlen)
        
            arr[i]=x[j++];
                
    
 

ps：只声明一个数组也可以实现；

递归的函数：

变为子问题排序。

void mergesort(int arr[],int l,int r)

    if(l<r)
    
        int mid=(l+r)/2;
        mergesort(arr,l,mid);        //分治，就是大数组从中间分成大小差不多的数组进行子问题的解决
        mergesort(arr,mid+1,r);
        merge(arr,l,mid,r);      //合并
    

以下是该题代码：

#include<bits/stdc++.h>
using namespace std;
int a[10000005];
typedef long long ll;
void merge(int arr[],int l,int mid,int r)

    int llen=mid-l+1,rlen=r-mid;
    int x[llen],y[rlen];
    for(int i=0;i<llen;i++)
    
        x[i]=arr[l+i];
    
    for(int i=0;i<rlen;i++)
    
        y[i]=arr[mid+1+i];
    
    int j=0,k=0;
    for(int i=l;i<=r;i++)
    
        if(x[j]<=y[k]&&j<llen&&k<rlen)
        
            arr[i]=x[j++];
        
        else if(x[j]>y[k]&&j<llen&&k<rlen)
        
            arr[i]=y[k++];
        
        else if(j>=llen)
        
            arr[i]=y[k++];
        
        else if(k>=rlen)
        
            arr[i]=x[j++];
                
    
 
void mergesort(int arr[],int l,int r)

    if(l<r)
    
        int mid=(l+r)/2;
        mergesort(arr,l,mid);
        mergesort(arr,mid+1,r);
        merge(arr,l,mid,r);
    

int main()

    int n,k;
    cin>>n>>k;
    for(int i=0;i<n;i++)
    
        cin>>a[i];
    
    mergesort(a,0,n-1);
    /*for(int i=0;i<n;i++)
    
        cout<<a[i]<<" ";
    */
    cout<<a[k-1]<<endl;
    return 0;

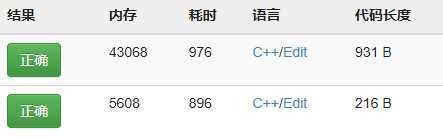
但是归并排序有一些缺陷，虽然和STL里的sort函数的复杂度均为O(nlogn)，但是内存方面归并排序要占的很多，由此可见归并排序也并不是理想的排序方法，尤其是数据多的时候。之后会更新堆排序（前提是我先学会...