P2934 [USACO09JAN]安全出行

Posted 2022-09-18 ajmddzp

 

图论瞎搞......

solution：

按例化简：给定一个无向图，保证单源最短路唯一，求每个点到1号点的最短路最后一条边被封锁的情况下的最短路

乍一看，应该是次短路，但是稍微用脚趾头想想都能发现不是次短路.....

然后就乱搞了一发。秉承着我们的口号

暴力碾标算，n方过百万

我试着搞了一发暴力：先求出最短路径树（很重要），然后对于每一个点的父亲（前一个节点）进行dij拓展，不走被封的边，然后遇到目标点就退出（思路来源：旅行者）

然后我发现，不仅仅会T，甚至这个思路就是错的！！！

1、为什么会T：旅行者那题相当于只找一个最短边权当做最短路，因此dij的拓展过程可以认为是O（1）的；

2、为什么会wa：来看样例：

 

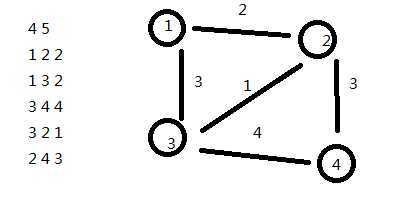
 我弄出来的最短路径树是这样的：

 

 

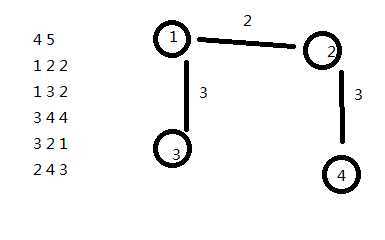
根据以上思路，只需要求出dis（最短路），还有从父亲节点拓展的dis，加起来即可。

 

但是，当走到2，拓展4的时候：拓展的非树边和之前的最短路加起来，变成了7！？

 

但是，如果换一条路走，答案应该是6......

 

所以，这个思路到此终结（我170+lines的代码啊！！！！）

 

正解：（对，没错，这里才开始正解）

 

首先，最短路径树的思路要保留，这里有一个比较玄学的式子：

min(dis(u,v)（边权）+dis（u）-dis（v）+dis（v)）；

 

 

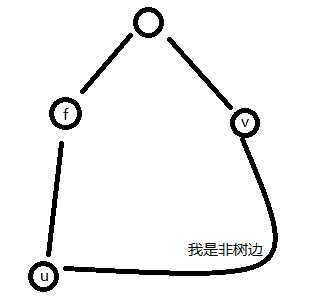
 要求根到f的路径径，只需要知道根到u的最短路-根到f的最短路（也就是f到u的一条路径）加上根到v的最短路，再加上u到v的边权，这样就完成了一次拓展。

于是，就维护这个式子，用并查集维护联通（据机房大佬说这是并查集缩变233）

• 把所有非树边 记录下来
• 枚举点
• 更新式子
• 维护连通
• 进行n-1次

就是这样....据说spfa会被卡？本人专门卡各种卡spfa.....

注意一下，要判断无解.....

 

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
int n,m;
inline int read()

    int x=0,f=1;char s=getchar();
    while(s>‘9‘||s<‘0‘)if(s==‘-‘)f=-1;s=getchar();
    while(s<=‘9‘&&s>=‘0‘)x=x*10+s-‘0‘;s=getchar();
    return f*x;

struct edge

    int to,next,dis;
e[maxn];
int cnt,head[maxn];
inline void addedge(int from,int to,int dis)

    e[++cnt].next=head[from];
    e[cnt].to=to;
    e[cnt].dis=dis;
    head[from]=cnt;

int fa[maxn];
int dis[maxn];
struct cmp

    bool operator ()(int a,int b)
    
        return dis[a]>dis[b];
    
;
priority_queue <int,vector<int>,cmp> q;
int vis[maxn];
inline void spfa(int s)

    for(int i=1;i<=n;i++)
    
        dis[i]=0x7fffffff;
        vis[i]=0;
    
    vis[s]=1;
    dis[s]=0;
    q.push(s);
    while(!q.empty())
    
        int u=q.top();
        q.pop();
        vis[u]=0;
        for(register int i=head[u];i;i=e[i].next)
        
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].dis)
            
                dis[v]=dis[u]+e[i].dis;
                fa[v]=u;
                if(vis[v]==0)
                
                    vis[v]=1;
                    q.push(v);
                
            
        
    


struct tree

    int u,v,w;
a[maxn];
bool cmp(tree a,tree b)

    return a.w<b.w;

int f[maxn],ans[maxn];
int num;
int find(int x)

    if(f[x]==x)
    return x;
    return f[x]=find(f[x]);

void solve(tree x)

    int u=x.u,v=x.v,t=x.w;
    while(find(u)!=find(v))
    
        num++;
        if(dis[find(u)]<dis[find(v)])
        swap(u,v);
        ans[find(u)]=min(ans[find(u)],t-dis[find(u)]);
        u=f[find(u)]=fa[find(u)];
    

int tot;
int main()

    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    
        int x,y,z;
        x=read();y=read();z=read();//scanf("%d%d%d",&x,&y,&z);
        addedge(x,y,z);
        addedge(y,x,z);
    
    spfa(1);
    for(int i=2;i<=cnt;i+=2)
    
        int u=e[i].to;
        int v=e[i-1].to;;
        if(u!=fa[v]&&v!=fa[u])
        
            a[++tot].u=u;
            a[tot].v=v;
            a[tot].w=e[i].dis+dis[u]+dis[v];
        
    
    
    sort(a+1,a+1+tot,cmp);
    for(int i=1;i<=n;i++)
    
        f[i]=i;
        ans[i]=2147483647;
    
    for(int i=1;i<=tot&&num<n-1;i++)
    
        solve(a[i]);
    
    for(int i=2;i<=n;i++)
    
        if(ans[i]!=2147483647)
        printf("%d\\n",ans[i]);
        else
        printf("-1\\n");
    
    return 0;