插值相关总结

Posted 2022-09-13 fangxiaoqi

　　插值的通俗解释就是一种用一些已知的数据去预测想要的数据的方法。

多项式插值

　　多项式插值是最常见的一种函数插值(插值函数为多项式)。

$$p_n(x) = a_0 + a_1x + a_2x^2 +  \\cdots  + a_nx^n$$

　　从几何上看可以理解为：已知平面上n+1个不同点，要寻找一条n次插值多项式函数$p(x)$通过曲线$f(x)$上已知的这n+1个点。使$p(x)$接近$f(x)$。

　　而将n个点代入多项式函数，则可用方程组表示，即

$$\\left\\\\beginarrayla_0+a_1 x_0+a_2 x_0^2+\\cdots+a_n x_0^n=y_0 \\\\ a_0+a_1 x_1+a_2 x_1^2+\\cdots+a_n x_1^n=y_1 \\\\ \\ldots \\ldots \\ldots \\ldots \\ldots \\ldots \\ldots \\ldots \\ldots \\ldots \\ldots \\ldots \\\\ a_0+a_1 x_n+a_2 x_n^2+\\cdots+a_n x_n^n=y_n\\endarray\\right.$$

　　当系数矩阵满秩时，有唯一解。系数矩阵的行列式为以范德蒙德行列式，因此只要$n+1$个点互不相同(意味着范德蒙德行列式不为0)，就一定能够解出系数方程，得到多项式函数的系数$a_0,a_1,...,a_n$。

$$\\det (A) = \\left| \\beginarray*20c
1&x_0&x_0^2& \\cdots &x_0^n&\\\\
1&x_1&x_1^2& \\cdots &x_1^n&\\\\
& \\cdots & \\cdots & \\cdots & \\cdots & \\cdot \\\\
1&x_n&x_n^2& \\cdots &x_n^n&
\\endarray \\right|\\rm ! = \\rm 0$$

 

　　插值多项式一般有两种常见的表达形式，一个是拉格朗日插值多项式，另一个是牛顿插值多项式。

拉格朗日插值

　　一般的多项式插值即求线性方程组的解即可，但是这样求解的复杂度比较高。

　　基于一般多项式插值的求解思想，拉格朗日插值法诞生了。

　　1779年英国数学家爱德华·华林于最早发现拉格朗日插值法。

　　不久后1783年，由莱昂哈德·欧拉再次发现。

　　直到1795年，拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法。

　　为了降低解决问题的复杂度，引入了“基函数”的概念。

　　首先构造一组基函数：

$$l_i(x) = \\frac\\left( x - x_0 \\right) \\cdots \\left( x - x_i - 1 \\right)\\left( x - x_i + 1 \\right) \\cdots \\left( x - x_n \\right)\\left( x_i - x_0 \\right) \\cdots \\left( x_i - x_i - 1 \\right)\\left( x_i - x_i + 1 \\right) \\cdots \\left( x_i - x_n \\right) = \\prod\\limits_\\beginarray*20c
j = 0\\\\
j \\ne i
\\endarray^n \\fracx - x_jx_i - x_j ,\\quad (i = 0,1, \\cdots ,n)$$

　　注：$\\fracx - x_jx_i - x_j$就是求解$p(x)$的$n+1$个基函数。如果对推导过程感兴趣，参考链接里有，很简单的。

　　$l_i(x)$是$n$次多项式，满足

$$l_i\\left( x_j \\right) = \\left\\ \\beginarray*20l
0&j \\ne i\\\\
1&j = i
\\endarray \\right.$$

　　令

$$L_n(x) = \\sum\\limits_i = 0^n y_i l_i(x) = \\sum\\limits_i = 0^n y_i \\left( \\prod\\limits_\\beginarray*20c
j = 0\\\\
j = i
\\endarray^n \\fracx - x_jx_i - x_j \\right)$$

　　这就是$n$次的拉格朗日插值多项式，且$n+1$的$n$次拉格朗日插值多项式是惟一的。

　　拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值，这样的多项式称为拉格朗日插值多项式。

　　数学上来说，拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。

　　&&：拉格朗日插值法在插值区间内插值的精度远远大于区间外的精度，所以，在区间外，拉格朗日插值一般是不准确的。

　　MATLAB：

function y=lagrange(x0,y0,x)
%n个数据以数组x0,y0输入，m个插值点以数组x输入，输出数组y为m个插值。
n=length(x0);m=length(x);
for i=m;
    z=x(i);
    s=0.0;
    for k=1:n
        p=1.0;
        for j=1:n;
            if j~=k
            p=p*(z-x0(j))/(x0(k)-x0(j));
            end
        end
        s=p*y0(k)+s;
    end
    y(i)=s;
end

牛顿插值

　　用拉格朗日插值法，如果增加新的节点，需要从头重新计算，而牛顿差值法机智的引入了差商的概念，使其在差值节点增加时便于计算。

1. 差商

　　差商：设有函数$f(x)$，$x_0,x_1,x_2, \\cdots $为一系列互不相同的点，称$\\fracf\\left(x_i\\right)-f\\left(x_j\\right)x_i-x_j(i \\neq j)$为$f(x)$关于点$x_i, x_j$的一阶差商，记为$f\\left[ x_i,x_j \\right]$。

　　即$$f\\left[x_i, x_j\\right]=\\fracf\\left(x_i\\right)-f\\left(x_j\\right)x_i-x_j$$

　　二阶差商即一阶差商的差商，即

$$f\\left[ x_i,x_j,x_k \\right] = \\fracf\\left[ x_i,x_j \\right] - f\\left[ x_j,x_k \\right]x_i - x_k$$

　　同理，$k$阶差商为：

$$f\\left[x_0, x_1, \\cdots, x_k\\right]=\\fracf\\left[x_0, x_1, \\cdots, x_k-1\\right]-f\\left[x_1, x_2, \\cdots, x_k\\right]x_0-x_k$$

　　而且，差商中各点的顺序是可以轮换的：

$$\\beginarraylf\\left[x_i, x_j\\right]=f\\left[x_j, x_i\\right] \\\\ f\\left[x_i, x_j, x_k\\right]=f\\left[x_i, x_k, x_j\\right]=f\\left[x_j, x_i, x_k\\right]\\endarray$$

2. 牛顿插值公式

　　①把差商定义式展开，得到差商公式表：

$$\\beginarraylf(x)=f\\left(x_p\\right)+f\\left[x, x_0\\right]\\left(x-x_p\\right) \\\\ f\\left[x, x_0\\right]=f\\left[x_0, x_1\\right]+f\\left[x, x_0, x_1\\right]\\left(x-x_2\\right) \\\\ f\\left[x, x_0, x_1\\right]=f\\left\\x_0, x_1, x_2, x_2\\right]+f\\left[x, x_0, x_1, x_2\\right]\\left(x-x_2\\right) \\\\ \\cdots \\\\ f\\left[x, x_0, \\cdots, x_n-1\\right]=f\\left\\x_0, x_1, \\cdots, x_n\\right]+f\\left[x, x_0, \\cdots, x_n\\right]\\left(x-x_n\\right)\\endarray$$

　　②自底向上归纳得到，

$$\\beginarraylf(x)=f\\left(x_1\\right)+f\\left[x_n, x_1\\right]\\left(x-x_1\\right) \\\\ +f\\left[x_n, x_1, x_2\\right]\\left(x-x_1\\right)\\left(x-x_1\\right)+\\cdots+f\\left[x_n, x_n \\cdots, x_n\\right]\\left(x-x_1\\right)\\left(x-x_1\\right) \\cdot\\left(x-x_n-1\\right) \\\\ +f\\left[x_n, x_n, \\cdots, x_1\\right]\\left(x-x_1\\right)\\left(x-x_1\\right) \\cdot\\left(x-x_n\\right)\\endarray$$

　　③由于最后一项含有未知数$x$，因此去掉作为余项，便可得到牛顿插值公式。

$$\\beginaligned N_n(x) &=f\\left(x_0\\right)+\\left(x-x_0\\right) f\\left[x_0, x_1\\right]+\\cdots \\\\ &+\\left(x-x_0\\right)\\left(x-x_1\\right) \\cdots\\left(x-x_n-1\\right) f\\left[x_0, x_1, \\cdots, x_n\\right] \\endaligned$$

　　其插值余项记为

$$\\beginaligned R_n(x) &=\\left(x-x_0\\right)\\left(x-x_1\\right) \\cdots\\left(x-x_n\\right) f\\left[x, x_0, x_1, \\cdots, x_n\\right] \\\\ &=\\omega_n+1(x) f\\left[x, x_0, x_1, \\cdots, x_n\\right] \\endaligned$$

　　对比拉格朗日插值法：

　　与拉格朗日插值法相比，牛顿插值法增加节点时，不需要重新计算，在某些情景下比拉格朗日插值法更好用，而且在计算余项时，牛顿插值的余项由于不需要导数，故$f(x)$是由离散点或者导数不存在时仍然适用，这是拉格朗日余项计算所不能比拟的。

　　差商与导数的关系为：

$$f\\left[x_0, x_1, \\cdots, x_n\\right]=\\fracf^(n)(\\xi)n !$$

　　其中，$\\xi \\in(\\alpha, \\beta), \\alpha=\\min _0 \\leq i \\leq n\\left\\x_i\\right\\, \\beta=\\max _0 \\leq i \\leq n\\left\\x_i\\right\\$

泰勒插值

　　此外，还有Taylor插值，不过，一般基本用不到。

　　泰勒多项式：

$$p_x(x) = f\\left( x_0 \\right) + f^\\prime \\left( x_0 \\right)\\left( x - x_0 \\right) + \\fracf^\\prime \\prime \\left( x_0 \\right)2!\\left( x - x_0 \\right)^2 +  \\cdots  + \\fracf^(n)\\left( x_0 \\right)n!\\left( x - x_0 \\right)^n$$ 

　　而泰勒插值的条件需要满足$0-n$阶导数可导：$p_n^(k)\\left( x_0 \\right) = f^(k)\\left( x_0 \\right),\\quad k = 0,1, \\cdots ,n$

　　但是，满足n阶可导这个条件过于苛刻，所以泰勒插值并不常用。

埃尔米特插值

　　不少实际的插值问题不但要求在节点上的函数值相等，而且还要求对应的导数值也相等，甚至要求高阶导数也相等，满足这种要求的插值多项式就是埃尔米特插值多项式。

　　这意味着，拟合曲线与实际曲线不仅都过点$\\left(x_i, y_i\\right),\\left(x_i+1, y_i+1\\right)$，而且两点处还有相同的切线。

　　设在节点$a \\leq x_0<x_1<\\cdots<x_n \\leq b$上，$y_j=f\\left(x_j\\right)$，$m_j=f^\\prime\\left(x_j\\right) \\quad(j=0,1, \\cdots, n)$

　　即满足条件：$H\\left(x_j\\right)=y_j, \\quad H^\\prime\\left(x_j\\right)=m_j, \\quad(j=0,1, \\cdots, n)$

　　这里共有$2n+2$个插值条件，可唯一确定一个次数不超过$2n+1$的多项式$H_2 n+1(x)=H(x)$，其形式为：

$$H_2 n+1(x)=a_0+a_1 x+\\cdots+a_2 n+1 x^2 n+1$$

　　采用拉格朗日插值多项式的基函数方法的思想：

　　先求出$2n+2$个插值基函数，每个基函数都是$2n+1$次多项式，且满足条件：

$$\\beginarrayl\\alpha_j\\left(x_k\\right)=\\delta_j k=\\left\\\\beginarrayll0, & j \\neq k \\\\ 1, & j=k\\endarray, \\quad \\alpha_j^\\prime\\left(x_k\\right)=0\\right. \\\\ \\beta_j\\left(x_k\\right)=0, \\quad \\beta_j^\\prime\\left(x_k\\right)=\\delta_j k \\quad(j, k=0,1, \\cdots, n)\\endarray$$

　　用基函数表示插值多项式：

$$H_2 n+1(x)=\\sum_j=0^n\\left[y_j \\alpha_j(x)+m_j \\beta_j(x)\\right]$$

　　由插值基函数所满足的条件，有$H_2 n+1\\left(x_k\\right)=y_k, \\quad H_2 n+1^\\prime\\left(x_k\\right)=m_k, \\quad(k=0,1, \\cdots, n)$

　　然后求出基函数$\\alpha_j(x)$与$\\beta_j(x)$

　　利用拉格朗日插值基函数$l_j(x)$，

　　令$\\alpha_j(x)=(a x+b) l_j^2(x)$

　　得到

$$\\beginarrayl\\alpha_j\\left(x_j\\right)=\\left(a x_j+b\\right) l_j^2\\left(x_j\\right)=1 \\\\ \\alpha_j^\\prime\\left(x_j\\right)=l_j\\left(x_j\\right)\\left[a l_j\\left(x_j\\right)+2\\left(a x_j+b\\right) l_j^\\prime\\left(x_j\\right)\\right]=0\\endarray$$

　　整理得

　　$$\\left\\\\beginarrayla x_j+b=1 \\\\ a+2 l_j^\\prime\\left(x_j\\right)=0\\endarray\\right.$$

　　解出

$$a=-2 l_j^\\prime\\left(x_j\\right), \\quad b=1+2 x_j l_j^\\prime\\left(x_j\\right)$$

　　由于

$$l_j(x)=\\frac\\left(x-x_0\\right) \\cdots\\left(x-x_j-1\\right)\\left(x-x_j+1\\right) \\cdots\\left(x-x_n\\right)\\left(x_j-x_0\\right) \\cdots\\left(x_j-x_j-1\\right)\\left(x_j-x_j+1\\right) \\cdots\\left(x_j-x_n\\right)$$

　　两边取对数再求导，得

$$l_j^\\prime\\left(x_j\\right)=\\sum_k=0 \\atop k \\neq j^n \\frac1x_j-x_k$$

　　于是，

$$\\alpha_j(x)=\\left(1-2\\left(x-x_j\\right) \\sum_k=0 \\atop k \\neq j^n \\frac1x_j-x_k\\right) l_j^2(x)$$

　　同理，得到

$$\\beta_j(x)=\\left(x-x_j\\right) l_j^2(x)$$

　　综上所述，埃尔米特插值多项式为：

$$\\left\\ \\beginarray*20l
H_2n + 1(x) = \\sum\\limits_j = 0^n \\left[ y_j\\alpha _j(x) + m_j\\beta _j(x) \\right] \\\\
y_j = f\\left( x_j \\right),m_j = f^\\prime \\left( x_j \\right)\\\\
\\alpha _j(x) = \\left( 1 - 2\\left( x - x_j \\right)\\sum\\limits_k = 0^n \\frac1x_j - x_k \\right)l_j^2(x),k \\ne j\\\\
\\beta _j(x) = \\left( x - x_j \\right)l_j^2(x)
\\endarray \\right..$$

　　仿照拉格朗日插值余项的证明方法，得到埃尔米特插值余项：

$$R(x)=f(x)-H_2 n+1(x)=\\fracf^(2 n+2)(\\xi)(2 n+2) ! \\omega_n+1^2(x)$$

 

　　$n$取1时，是一个非常重要的特例，即两点三次埃尔米特插值，比较典型和常用(4个基函数均为三次多项式，$n=1$)

　　插值基函数满足条件：

$$\\beginarrayl\\alpha_k\\left(x_k\\right)=1, \\quad \\alpha_k\\left(x_k+1\\right)=0, \\quad \\alpha_k^\\prime\\left(x_k\\right)=\\alpha_k^\\prime\\left(x_k+1\\right)=0 \\\\ \\alpha_k+1\\left(x_k\\right)=0, \\quad \\alpha_k+1\\left(x_k+1\\right)=1, \\quad \\alpha_k+1^\\prime\\left(x_k\\right)=\\alpha_k+1^\\prime\\left(x_k+1\\right)=0 \\\\ \\beta_k\\left(x_k\\right)=\\beta_k\\left(x_k+1\\right)=0, \\beta_k^\\prime\\left(x_k\\right)=1, \\quad \\beta_k^\\prime\\left(x_k+1\\right)=0 \\\\ \\beta_k+1\\left(x_k\\right)=\\beta_k+1\\left(x_k+1\\right)=0, \\beta_k+1\\left(x_k\\right)=0, \\quad \\beta_k+1^\\prime\\left(x_k+1\\right)=1\\endarray$$

　　两点三次埃尔米特插值多项式为：

$$H_3(x)=y_k \\alpha_k(x)+y_k+1 \\alpha_k+1(x)+m_k \\beta_k(x)+m_k+1 \\beta_k+1(x)$$

　　余项为：

$$R_3(x)=\\frac14 ! f^(4)(\\xi)\\left(x-x_k\\right)^2\\left(x-x_k+1\\right)^2, \\quad \\xi \\in\\left(x_k, x_k+1\\right)$$

function y-hermite(x0,y0,y1,x);
%x0,y0为样本点数据，y1为导数指，m个插值点以数组x输入，输出数组y为m个插值
n=length(x0);
m=length(x);
for k=1:m;
    yy=0.0;
    for i=1:n
        h=1.0;
        a=0.0;
        for j=i:n
            if j~=i
                h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2; 
                a=1/(x0(i)-x0(j))+a;
            end
        end
        yy=yy+h*((x0(i)-x0(k))*(2*a*y0(i)-y(i))+y0(i));
    end
    y(k)=yy;
end

分段插值

　　分段插值：对每一个分段区间$(x_i,x_i + 1)$分别进行插值，则最后所得插值函数为分段函数。

　　很常用！

　　对于分段插值，我们主要探讨分段低次插值，因为高次插值存在病态性质，会出现大幅度波动现象，不能很好地拟合。

　　这就是个高次插值的图像，可以看出到了$x \\pm 5$附近时，拟合曲线偏离实际曲线很远。

分段线性插值

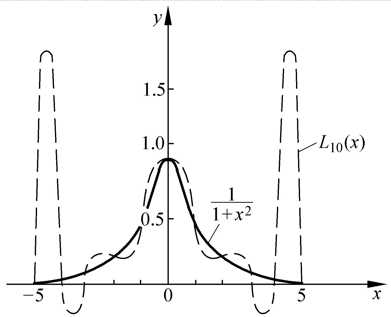
　　分段线性插值即把每两个相邻的节点用直线连起来，这样形成的折线就是分段线性插值函数，记作$I_n(x)$，它满足$I_n\\left(x_i\\right)=y_i$，且$I_n(x)$在每个小区间$\\left[x_i, x_i+1\\right]$上是线性函数。$(i=0,1, \\cdots, n)$

$$I_n(x)=\\sum_i=0^n y_i l_i(x)$$

$$l_i(x) = \\left\\ \\beginarray*20l
\\fracx - x_i - 1x_i - x_i - 1,&x \\in \\left[ x_i - 1,x_i \\right]\\rm i = 0\\\\
\\fracx - x_i + 1x_i - x_i + 1,&x \\in \\left[ x_i,x_i + 1 \\right]\\rm i = n\\\\
0,&else
\\endarray\\rm \\right.$$

　　用$I_n(x)$计算$x$点的插值时，只用到$x$左右的两个节点，计算量与节点数$n$无关。但$n$越大，分段越多，插值误差越小。
　　MATLAB：

$$\\mathrmy=\\text interp 1\\left(\\mathrmx 0, \\mathrmy0, \\mathrmx, \\text ‘method ^\\prime\\right)$$

　　method：

nearest	最近项插值
linear	线性插值
spline	逐段3次样条插值
cubic	保凹凸性3次插值

n=11;  m=61;
x=-5:10/(m-1):5;
y=1./(1+x.^2);
z=0*x;
x0=-5:10/(n-1):5;
y0=1./(1+x0.^2);
y1=interp1(x0, y0, x);%interp1(x0,y0,x)为Matlab中现成的分段线性插值程序
plot(x, z, ‘r‘, x, y, ‘k:‘, x, y1, ‘r‘)
gtext(‘Piece. –linear.‘), gtext(‘y=1/(1+x^2)‘)
title(‘Piecewise Linear‘)

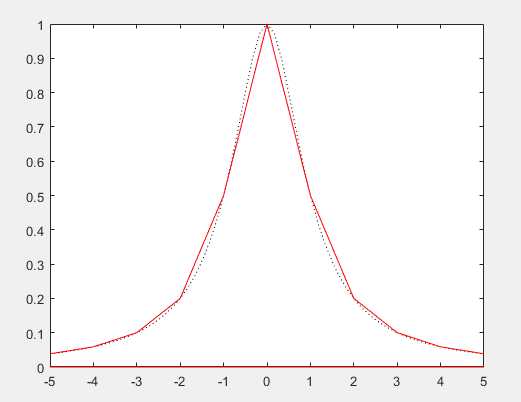
分段三次埃尔米特插值

　　分段差值简单易行，又克服了Runge现象，但它却导致一阶导数不连续，为了克服线性插值一阶导数不连续的缺点，可以使用分段三次埃尔米特插值。

　　分段三次埃尔米特插值函数即导数连续的分段插值函数。
　　根据两点三次埃尔米特插值多项式，得到$I_h(x)$在$\\left[x_k, x_k+1\\right]$的表达式为：

$$I_h(x) = \\left( \\fracx - x_k + 1x_k - x_k + 1 \\right)^2\\left( 1 + 2\\fracx - x_kx_k + 1 - x_k \\right)f_k + \\left( \\fracx - x_kx_k + 1 - x_k \\right)^2 \\cdot \\left( 1 + 2\\fracx - x_k + 1x_k - x_k + 1 \\right)f_k + 1 + \\left( \\fracx - x_k + 1x_k - x_k + 1 \\right)^2\\left( x - x_k \\right)f^\\prime \\left( x_k \\right) + \\left( \\fracx - x_kx_k + 1 - x_k \\right)^2\\left( x - x_k + 1 \\right)f_k + 1^\\prime $$
　　若在整个区间$[a, b]$上定义一组分段三次插值基函数$\\alpha_j(x)$及$\\beta_j(x)$,$(j=0,1, \\cdots, n)$，则$I_h(x)$可表示为：

　　$$I_h(x)=\\sum_j=0^n\\left[f_j \\alpha_j(x)+f_j^\\prime \\beta_j(x)\\right]$$

　　其中$\\alpha_j(x)$，$\\beta_j(x)$分别表示为

$$\\alpha _j(x) = \\left\\ \\beginarray*20c
\\left( \\fracx - x_j - 1x_j - x_j - 1 \\right)^2\\left( 1 + 2\\fracx - x_jx_j - 1 - x_j \\right)x_j - 1 \\le x \\le x_j\\\\
\\beginarrayl
\\left( \\fracx - x_j + 1x_j - x_j + 1 \\right)^2\\left( 1 + 2\\fracx - x_jx_j + 1 - x_j \\right)x_j \\le x \\le x_j + 1\\\\
\\rm 0
\\endarray
\\endarray \\right.$$

$$\\beta _j(x) = \\left\\ \\beginarray*20c
\\left( \\fracx - x_j - 1x_j - x_j - 1 \\right)^2\\left( x - x_j \\right)x_j - 1 \\le x \\le x_j\\\\
\\beginarrayl
\\left( \\fracx - x_j + 1x_j - x_j + 1 \\right)^2\\left( x - x_j \\right)x_j \\le x \\le x_j + 1\\\\
\\rm 0
\\endarray
\\endarray \\right.$$

　　$I_h(x)$可表示为：

$$\\beginarraycI_h(x)=f_k \\alpha_k(x)+f_k+1 \\alpha_k+1(x)+f_k^\\prime \\beta_k(x)+f_k+1^\\prime \\beta_k+1(x) \\\\ \\left(x_k \\leq x \\leq x_k+1\\right)\\endarray$$
　　MATLAB：来自官方文档 https://ww2.mathworks.cn/help/matlab/ref/pchip.html

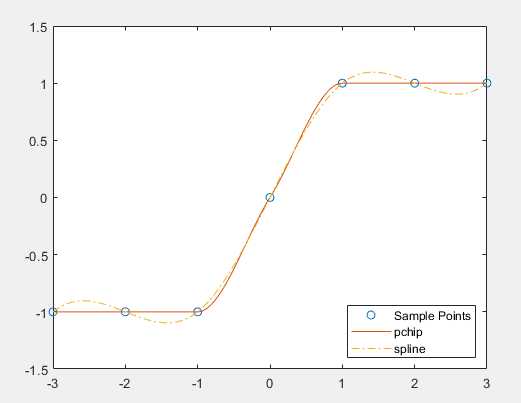
　　将 spline 和 pchip 为两个不同函数生成的插值结果进行比较。

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:.01:3;
p = pchip(x,y,xq1); %分段三次埃尔米特插值
s = spline(x,y,xq1); %逐段3次样条插值
plot(x,y,‘o‘,xq1,p,‘-‘,xq1,s,‘-.‘) 
legend(‘Sample Points‘,‘pchip‘,‘spline‘,‘Location‘,‘SouthEast‘)

　　为了避免高次插值可能出现的大幅度波动现象，在实际应用中通常采用分段低次插值来提高近似程度，比如可用分段线性插值或分段三次埃尔米特插值来逼近已知函数，但它们的总体光滑性较差。为了克服这一缺点，一种全局化的分段插值方法，即三次样条插值，下面我们单独说一下。

三次样条插值

　　分段插值的优点是误差小，稳定性高，但是曲线的光滑性不好，而许多实际问题需要插值曲线有较高阶的整体光滑性，理论上是可以使用高次埃尔米特插值或分段高次埃尔米特插值，但是必须知道每一个点的导数是不现实的。所以，样条插值诞生了。理论推导参考：https://www.cnblogs.com/duye/p/8671820.html

　　MATLAB：

1、y=interp1($x_0$,$y_0$,$x$,‘spline‘);
% spline改成linear，则变成线性插值
2、y=spline($x_0$,$y_0$,$x$);
% 这个是根据己知的x，y数据，用样条函数插值出$x_i$处的值。
% 由己知的x，y数据，求出它的样条函数表达式，不过该表达式不是用矩阵直接表示，要求点x`的值，要用函数
3、pp=csape(x,y,conds); y=ppval(pp,$x$);
% 各种边界条件的三次样条插值
conds是指边界条件，边界类型可为:
①‘complete‘： 给定边界一阶导数，默认的边界条件
②‘not-a-knot‘：非扭结条件，不用给边界值.
③‘periodic‘： 周期性边界条件，不用给边界值.
④‘second‘： 给定边界二阶导数.
⑤‘variational‘： 自然样条(边界二阶导数为[0,0]。

　　

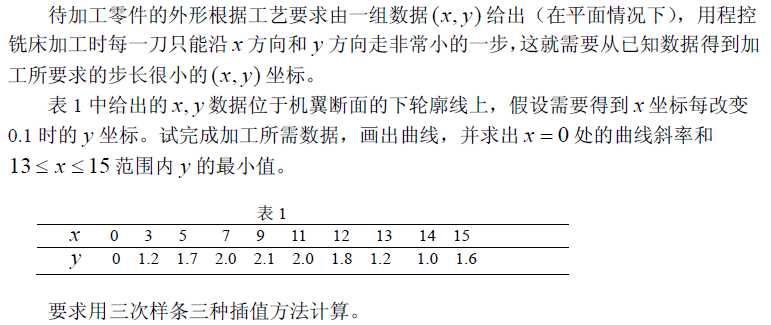
clear
clc 
x0=[0,3,5,7,9,11,12,13,14,15]; 
y0=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6]; 
t=0:0.05:15;
y1=spline(x0,y0,t); 
dy1=(spline(x0,y0,0.0001)-spline(x0,y0,0))/0.0001%x=0处斜率 
min1=min(spline(x0,y0,13:0.001:15))%13到15最小值 
figure
plot(x0,y0,‘ro‘,t,y1);%画出曲线 
title(‘三次样条插值‘); 

部分参考链接：

[1]:https://www.cnblogs.com/BlueMountain-HaggenDazs/p/4271977.html

[2]:https://www.cnblogs.com/duye/p/8671820.html

[3]:https://wenku.baidu.com/view/53498f69492fb4daa58da0116c175f0e7cd1190c.html