题解 SP22

Posted 2022-09-11 s-t-a-r-d-u-s-t

这里有几个关于重心，垂心的定理，我将其称作Aladdin Sane定理：\(→GA+→GB+→GC=→0(1)\)；

\(→HA·→HB=→HB·→HC=→HA·→HC(2)\)；

\(GA=2GZ(3)\)；

其中\(G\)是重心，\(Z\)是\(BC\)的中点，\(P\)是任意点，自然也可以是垂心。这几个定理可以大大减少计算量。或者说，没这几个定理根本算不出来。

那个箭头是向量符号，我不会打没办法。

推导不推了，基本的高一知识，可以自己去研究。

另外我们从学向量就知道，建系是一种极其好用的方法，可以解决掉\(80%\)以上的向量题。

于是我们思路就出来了。接下来我将一步步进行计算。

先画一个三角形。如图（1）：

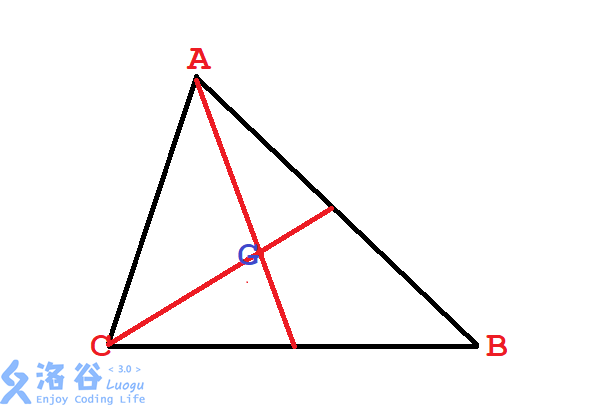
\(BC=a\)，设\(Ga=l,Gb=m,Gc=n\),含义如题。这些已知。再设\(b,c,xg,yg,xa,ya\),含义同上。

以\(C\)为原点，\(CB\)为\(x\)正半轴建立直角坐标系，得\(C(0,0),B(a,0)\);

由（3），显然\(yg=l,ya=3l.\)

由（1），\(→GA=(xa-xg,2l),→GB=(a-xg,-l),→GC=(-xg,-l)\);

即\(a+xa=3xg,xa=3xg-a\);

\(A(3xg-a,3l),G(xg,l)\);

那么现在只剩\(xg\)一个未知数了，可以再列个方程：

直线AC解析式：\(\frac3la-3xg·x+y=0\);

由cehi公式（两点间距离公式），\(Gb=m=\frac|l+\frac3xgla-3xg|\sqrt1+(\frac3la-3xg)^2\),即\(m^2=\fraca^2l^29l^2+(a-3xg)^2\).

得\(3xg-a=±\sqrt\fraca^2l^2m^2-9l^2\);

这儿有个正负号。怎么办？

看看图就好了。显然根号为非负，因此±取正或取负问题即A点x坐标正负问题。显然，由钢穴定理（cos定理）\(∠C<\pi/2\),即\(\fraca^2+b^2-c^22ab>0\)时\(xa>0\).故代码加入一行讨论：

if(a*a+b*b-c*c<0)
    xa=-xa;

即\(xa=±\sqrt\fraca^2l^2m^2-9l^2,xg=a/3±(\sqrt\fraca^2l^2m^2-9l^2)/3\)且与\(xa\)同号。为方便表示（正负号懒得打），以下将\(xa,xg\)看作已知量。

则由银河帝国第二定律（勾股定理），\(b=\sqrtxa^2+9l^2=al/m;\)由hijkl对称性：\(c=al/n\).

三边知道求面积，海伦-秦九韶立即见效！

海伦-秦九韶公式：\(S=\sqrtp(p-a)(p-b)(p-c),p=(a+b+c)/2\),不作证明。

由海伦-秦九韶，\(p=(a+al/m+al/n)/2,S=\sqrtp(p-a)(p-b)(p-c)\).

先把S输出来，发现是对的，说明我前面的推导没问题。很好！可是还有个大麻烦，我们还要求重心到垂心的距离。图（2）：

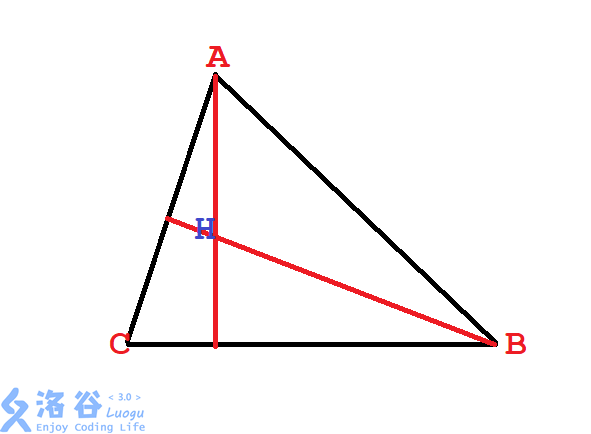
思路大同小异：Sane（2）还没有用，就用它求出垂心，再用距离公式算出GH。

设\(H(x,y)\)（变量名有点草率）；

易得\(→HA=(xa-x,3l-y),→HB=(a-x,-y),→HC=(\fracxa+a3-x,l-y)\);

进行向量计算，得\((xa-x)(a-x)+y(y-3l)=x(x-a)+y^2=x(x-xa)+y(y-3l)\);

千万不要同时除以\((xa-x)\),因为H是垂心，显然x是等于xa的。

按这个思路去解，得\(x=xa,y=\fraca·xa-xa^23·l\).

故\(HG=\sqrt((a-2·xa)/3)^2+(l-\fraca·xa-xa^23·l)^2\).

这样就算完可以输出了。反正是电脑来计算，结果多复杂都没事。

代码：

#include<bits/stdc++.h>
using namespace std;
int main()

    int t;
    cin>>t;
    while(t--)
    
        double a,l,m,n;
        cin>>a>>l>>m>>n;
        double b=a*l/m,c=a*l/n;
        double p=(a+b+c)/2;
        printf("%.3lf ",sqrt(p*(p-a)*(p-b)*(p-c)));
        //面积
        double xa=sqrt(a*a*l*l/m/m-9*l*l);
        if(a*a+b*b-c*c<0)
            xa=-xa;
        double xg=a/3+xa/3,yg=(a*xa-xa*xa)/3/l;
        printf("%.3lf\n",sqrt((xg-xa)*(xg-xa)+(l-yg)*(l-yg)));
        //HG距离
    
    
    return 0;

（完）