弗洛伊德求每个顶点到其余各顶点的最短路径
Posted yshun
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了弗洛伊德求每个顶点到其余各顶点的最短路径相关的知识,希望对你有一定的参考价值。
以5 a b 7 a d 4 b c 2 b d 3 c a 3 c b 2 c d 1 d c构造有向图并找出每个顶点到其余顶点的最短路径
#include <stdio.h> #include <stdlib.h> #define MaxVertexNum 100 #define BIG 100 typedef char VertexType;//顶点节点的数据类型 typedef int EdgeType;//边权值的数据类型 typedef struct VertexType Vertex[MaxVertexNum];//顶点表 EdgeType Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵,边表 int vertexnum,arcnum;//顶点数和边数 MGraph;//邻接矩阵的存储结构 int Locate(VertexType v) if(v>=97)return (int)v-97; else return (int)v-65; //将顶点转换为相应的位置 void CreatGraph(MGraph &M) EdgeType e; VertexType v1,v2; printf("输入节点数和边数:"); scanf("%d %d",&M.vertexnum,&M.arcnum); printf("输入节点:"); for(int i=0;i<M.vertexnum;i++) getchar(); scanf("%c",&M.Vertex[i]); for(int i=0;i<M.vertexnum;i++) for(int j=0;j<M.vertexnum;j++) M.Edge[i][j]=BIG; if(i==j) M.Edge[i][j]=0; fflush(stdin);//清除缓存,防止下一次的scanf()函数失效 printf("输入路径的权值及其两个节点:\\n"); for(int i=0;i<M.arcnum;i++) scanf("%d %c %c",&e,&v1,&v2); M.Edge[Locate(v1)][Locate(v2)]=e; //构造一个有向图 void PrintGraph(MGraph &M) printf("邻接矩阵\\n"); for(int i=0;i<M.vertexnum;i++) printf(" %c ",M.Vertex[i]); for(int j=0;j<M.vertexnum;j++) if(M.Edge[i][j]!=BIG) printf("%d ",M.Edge[i][j]); elseprintf("∞ "); printf("\\n"); //打印邻接矩阵 void visited(int v) printf("%c ",v+‘a‘); //访问当前节点的位置 void Floyd(MGraph &M,int path[MaxVertexNum][MaxVertexNum]) int A[M.vertexnum][M.vertexnum];//记录数组中任意两个顶点之间的最短距离 for(int i=0;i<M.vertexnum;i++) for(int j=0;j<M.vertexnum;j++) A[i][j]=M.Edge[i][j]; path[i][j]=-1; for(int k=0;k<M.vertexnum;k++) for(int j=0;j<M.vertexnum;j++) for(int i=0;i<M.vertexnum;i++) if(A[i][j]>A[i][k]+A[k][j]) A[i][j]=A[i][k]+A[k][j]; path[i][j]=k; printf("A矩阵\\n"); for(int i=0;i<M.vertexnum;i++) printf(" "); for(int j=0;j<M.vertexnum;j++) printf("%d ",A[i][j]); printf("\\n"); printf("path矩阵\\n"); for(int i=0;i<M.vertexnum;i++) printf(" "); for(int j=0;j<M.vertexnum;j++) printf("%d ",path[i][j]); printf("\\n"); int main() MGraph M; CreatGraph(M); PrintGraph(M); int path[MaxVertexNum][MaxVertexNum];//记录当前两节点间要经过的中间节点 Floyd(M,path);
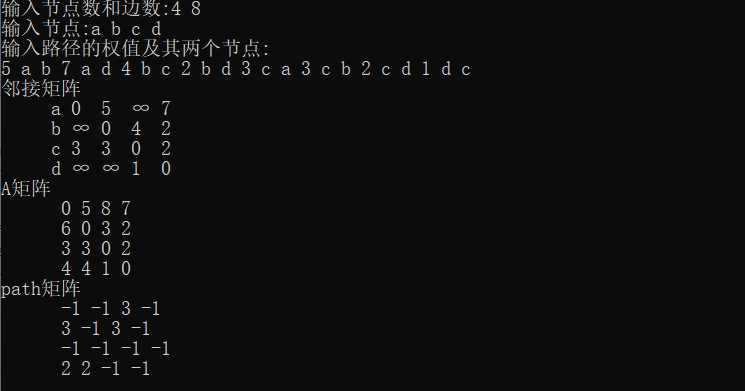
以上是关于弗洛伊德求每个顶点到其余各顶点的最短路径的主要内容,如果未能解决你的问题,请参考以下文章