从正则表达式到 NFA 到 DFA 到最简 DFA
Posted metatronwings
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从正则表达式到 NFA 到 DFA 到最简 DFA相关的知识,希望对你有一定的参考价值。
从正则表达式到 NFA 到 DFA 到最简 DFA (二)
NFA $ \\rightarrow $ DFA (子集构造法)
这里我们用一个例子来解释。
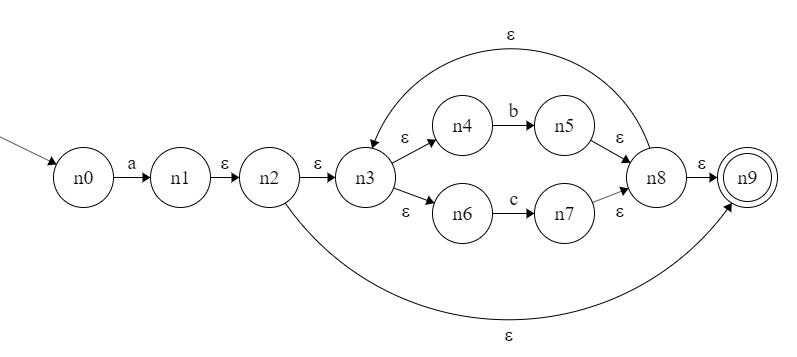
如上图所示,这是上一篇文章中的正则表达式化成的 NFA,这里拿来接着用。
我们首先看开始状态 n0。n0 在接收了一个字符 a 之后可以转换到 n1,这个时候我们要看 n1 是否存在 $ \\varepsilon $ 转移。若存在,则递归的将所有能 $ \\varepsilon $ 转移的状态添加到一个集合里(包括 n1)。然后再看我们所创造的这个集合是否可以接收字符,接收字符后转移到的状态是否还有 $ \\varepsilon $ 转移,依此类推。
拿这个图举例子就是:
$ n0 \\xrightarrowa n1 ?$
n1 能 $ \\varepsilon $ 转换到的状态是 q1,即 \\(\\ n1, n2, n3, n4, n6, n9 \\ : q1\\) ,记 \\(\\n0\\: q0\\)
$ q1 \\xrightarrowb n5 $
n5 能 $ \\varepsilon $ 转移到的状态是 q2,即 \\(\\ n5, n8, n9, n3, n4, n6 \\ : q2\\)
\\(q2 \\xrightarrow... \\...\\ : q3?\\)
我们构造的这个集合就叫做 $ \\varepsilon - $闭包。
工作表算法
q0 ← ?-闭包(n0)
Q ← q0
workList ← q0
while (workList != [])
remove q from workList
foreach char c
t ← ?-闭包(delta(q, c))
D[q, c] ← t
if t 不属于 Q
add t to Q and workList最终,Q 中的所有集合就是我们要求的 DFA 中的每个状态。再将状态转移连好,转换后的 DFA 就形成了。
以上是关于从正则表达式到 NFA 到 DFA 到最简 DFA的主要内容,如果未能解决你的问题,请参考以下文章