树状数组模板

Posted 2020-11-11 End_donkey

树状数组 1 单点修改，区间查询

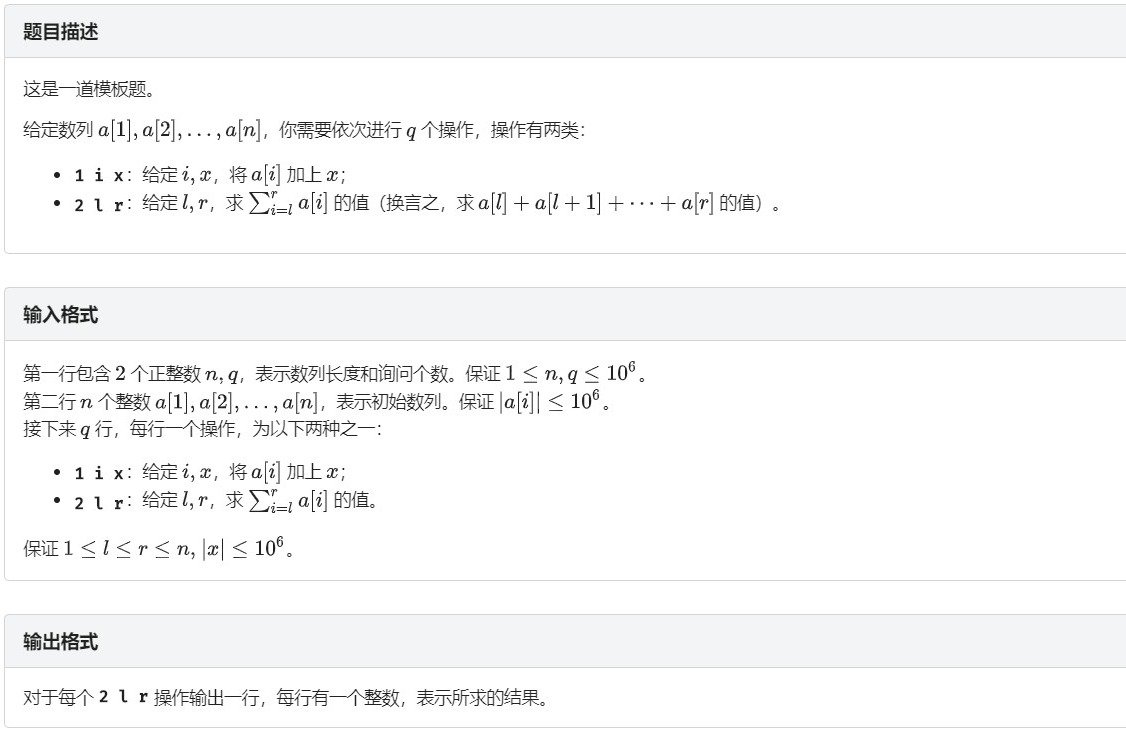
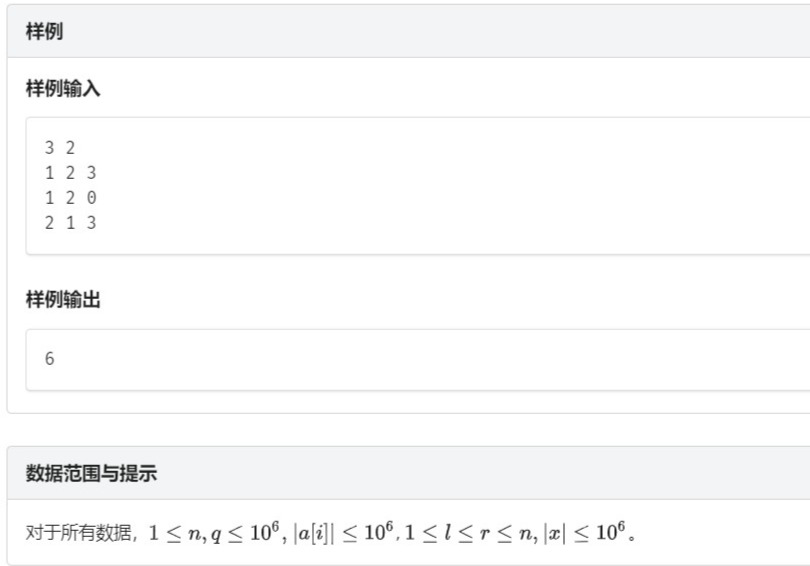
这个没啥好讲的，修改加查询即可，查询时利用前缀和相减即可。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000010;
int n,q,u,v,k,a[maxn];
long long c[maxn];
int lowbit(int x){
    return x&(-x);
}
void add(int x,long long y){
    for(;x<=n;x+=lowbit(x)) c[x]+=y;
}
long long ask(int x){
    long long ans=0;
    for(;x;x-=lowbit(x)) ans+=c[x];
    return ans;
}
int main(){
    scanf("%d %d",&n,&q);
    for(int i=1;i<=n;++i){
        scanf("%d",&a[i]);
        add(i,a[i]);
    }
    while(q--){
        scanf("%d %d %d",&k,&u,&v);
        if(k==1){
            add(u,v);
        }
        else{
            printf("%lld\n",(ask(v)-ask(u-1)));
        }
    }
    return 0;
}

树状数组 2 区间修改，单点查询

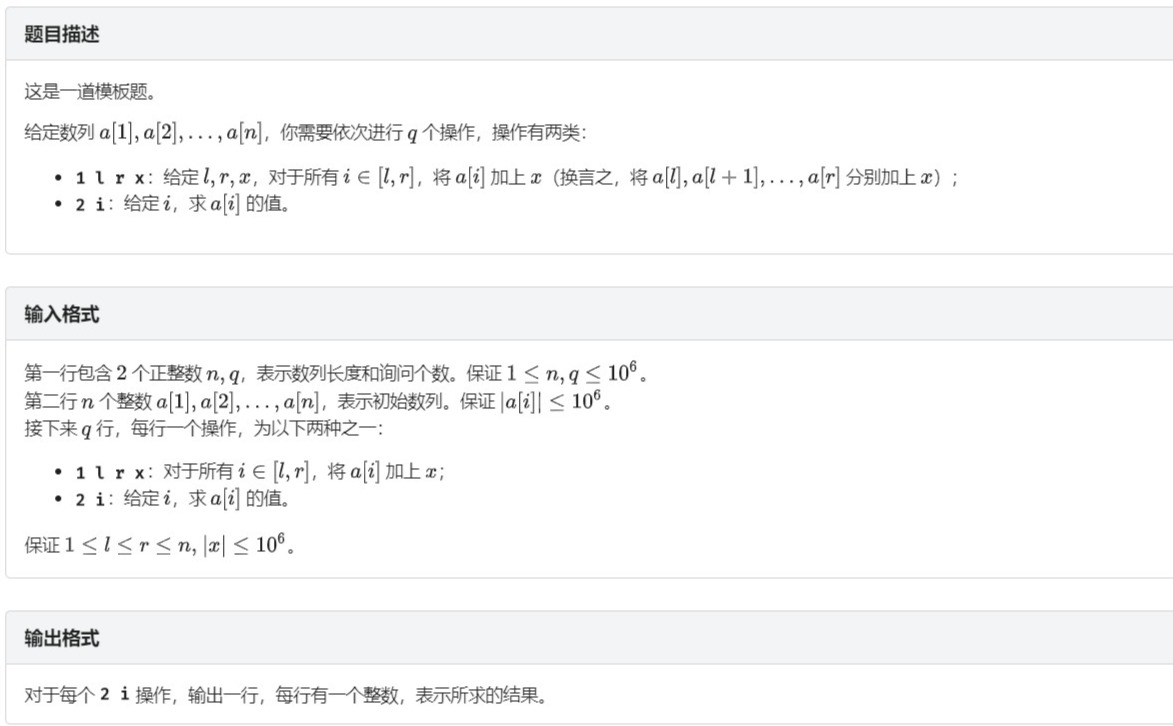
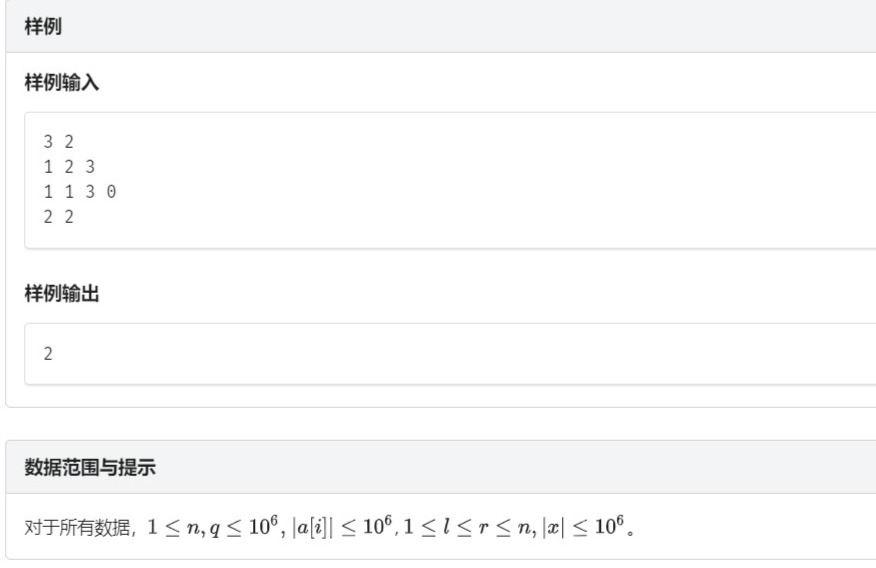
这道题还是比较简单的，树状数组仅支持“单点修改”那么我们便需要在做出一些转化来解决这个问题，我们可以新建一个数组b，起初全为0，对于每一条修改语句 "1,l,r,x"我们可以转换为

1.把b[l]加上d

2.把b[r+1]减去d

其思路就类似于差分，我们在统计前缀和时就相当将l到r这个区间加上了d，那么我们就用树状数组来维护b数组的前缀和(单点修改即可达到目的)，因为各次操作之间具有可累加性，所以在树状数组上查询b[1~x]就的处理到目前位置1指令在a[x]上操作的数值总和，再加上a[x]的值我们就得到了答案。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000010;
int n,q,u,v,k,a[maxn];
long long c[maxn];
int lowbit(int x){
    return x&(-x);
}
void add(int x,long long y){
    for(;x<=n;x+=lowbit(x)) c[x]+=y;
}
long long ask(int x){
    long long ans=0;
    for(;x;x-=lowbit(x)) ans+=c[x];
    return ans;
}
int main(){
    scanf("%d %d",&n,&q);
    for(int i=1;i<=n;++i){
        scanf("%d",&a[i]);
    }
    while(q--){
        scanf("%d",&k);
        if(k==1){
            scanf("%d %d %d",&u,&v,&k);
            add(u,k);
            add(v+1,-k);
        }
        else{
            scanf("%d",&u);
            printf("%lld\n",(ask(u)+(long long)a[u]));
        }
    }
    return 0;
}

树状数组 3 区间修改，区间查询

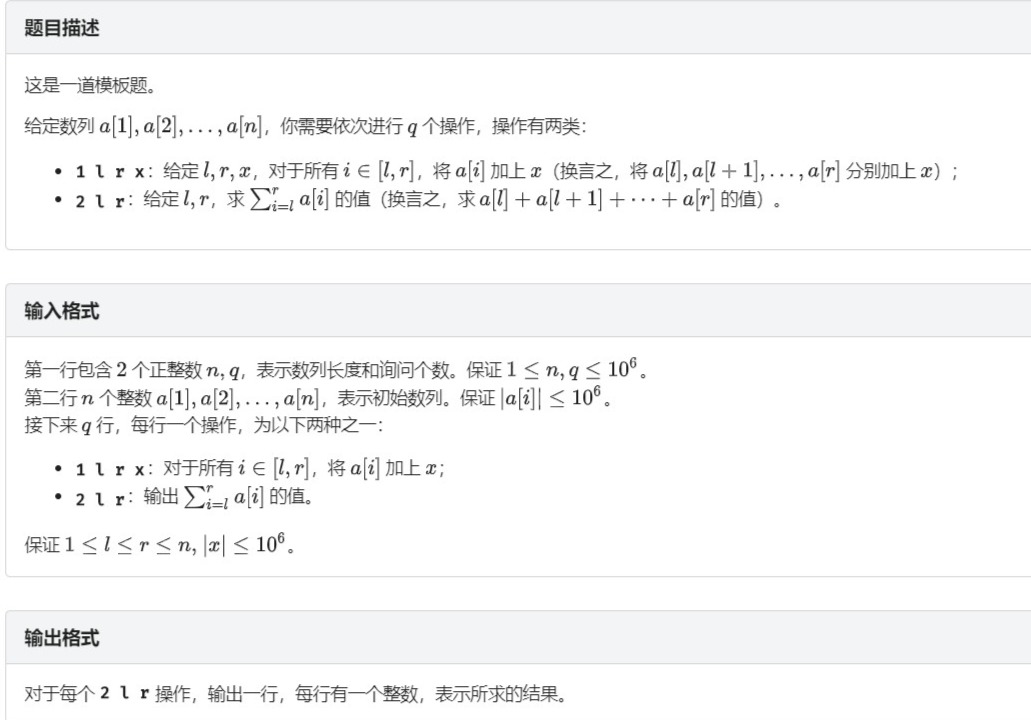
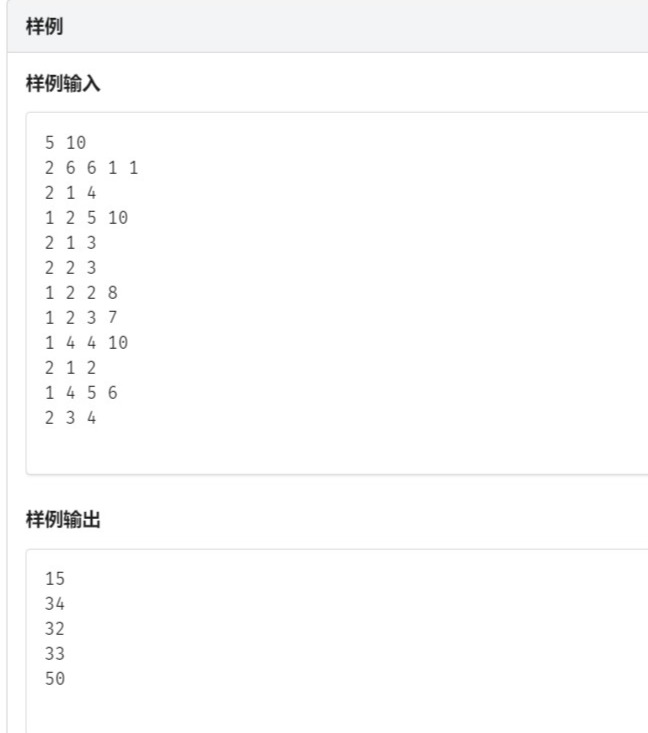
对于这道题其实和树状数组 2是差不多的，在树状数组2中我们用数组数组维护了一个数组b，对于每条指令“ 1，l，r，x”把b[l]加上d，再把b[r+1]减去d，我们以及讲了数组的前缀和 \(\sum_{i=1}^x\) b[i] 就是经过这些指令后a[x]增加的值。那么序列a的前缀和 a[1~x]整体增加的值就是：

\(\sum_{i=1}^x\) \(\sum_{j=1}^i\) b[j]

上式可以改写为

\(\sum_{i=1}^x\) \(\sum_{j=1}^i\) b[j] = \(\sum_{i=1}^x\) (x-i+1) \(\times\) b[i]= \(\sum_{i=1}^x\) b[i] - \(\sum_{i=1}^x\) i \(\times\) b[i]

本题我们可以增加一个树状数组维护i \(\times\) b[i]的前缀和 \(\sum_{i=1}^x\) i \(\times\) b[i]
，上式就可以直接计算了。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000010;
int n,q,u,v,k,a[maxn];
long long c[3][maxn],sum[maxn];
int lowbit(int x){
    return x&(-x);
}
void add(int num ,int x,long long y){
    for(;x<=n;x+=lowbit(x)) c[num][x]+=y;
}
long long ask(int num ,int x){
    long long ans=0;
    for(;x;x-=lowbit(x)) ans+=c[num][x];
    return ans;
}
int main(){
    scanf("%d %d",&n,&q);
    for(int i=1;i<=n;++i){
        scanf("%d",&a[i]);
        sum[i]=sum[i-1]+a[i];
    }
    while(q--){
        scanf("%d",&k);
        if(k==1){
            scanf("%d %d %d",&u,&v,&k);
            add(0,u,k);
            add(0,v+1,-k);
            add(1,u,(long long)u*k);
            add(1,v+1,-((long long)(v+1)*k));
        }
        else{
            scanf("%d %d",&u,&v);
            long long ans=sum[v]+(v+1)*ask(0,v)-ask(1,v);
            ans-=sum[u-1]+u*ask(0,u-1)-ask(1,u-1);
            printf("%lld\n",ans);
        }
    }
    return 0;
}